Многосеточный метод

Многосеточный (МС, англ. multigrid) метод — метод решения системы линейных алгебраических уравнений, основанный на использовании последовательности уменьшающихся сеток и операторов перехода от одной сетки к другой. Сетки строятся на основе больших значений в матрице системы, что позволяет использовать этот метод при решении эллиптических уравнений даже на нерегулярных сетках.

Основы метода

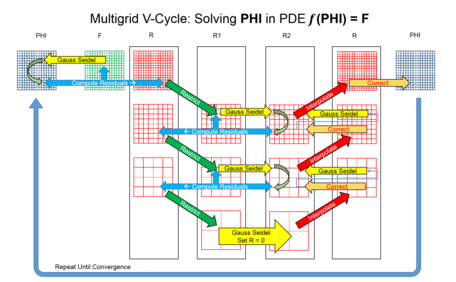
Предположим, что необходимо решить систему вида

$Au=f,$

где $A$ — $n \times n$ матрица с элементами $a_{ij}$. Для удобства сопоставим индексы с узлами сетки, таким образом $u_i$ представляет собой значение $u$ в узле $i$. Множество узлов сетки обозначим как $\Omega=\left\{1,\,2,\,\dots,\,n\right\}$. Основная идея многосеточных методов состоит в том, что ошибка $e$, которая не может быть устранена методами релаксации, должна быть убрана с помощью коррекции из решения на грубой сетке.

Используя верхний индекс в качестве номера уровня введем следующие обозначения:

• Последовательность сеток $\Omega = \Omega^1 \supset \Omega^2 \supset \dots \supset \Omega^M$, причем $\Omega^k = C^k \cup F^k,\quad C^k \cap F^k = \emptyset, \quad \Omega^{k+1} \equiv C^k$.
• Сеточные операторы $A=A^1,\,A^2,\,\dots,\,A^M$.
• Операторы интерполяции $P^k, k=1,\,2,\,\dots,\,M-1$.
• Операторы сглаживания $S^k, k=1,\,2,\,\dots,\,M-1$.

Все эти компоненты многосеточного метода строятся на первом этапе, известном как этап построения

Этап построения

1. Приравнять $k = 1$.
2. Разделить $\Omega^k$ на непересекающиеся множества $C^k$ и $F^k$.
   1. Приравнять $\Omega^{k+1} = C^k$.
   2. Построить оператор интерполяции $P^k$.
3. Построить $A^{k+1}=\left(P^k\right)^T A^k P^k$.
4. Построить если необходимо $S^k$.
5. Если сетка $\Omega^k$ достаточно мала, приравнять $M = k+1$ и остановиться. Иначе $k = k + 1$ и переход на шаг 2.

Как только этап построения завершен, может быть определен рекурсивный цикл построения решения:

Алгоритм: $MGV \left(A^k,\, P^k,\, S^k,\, u^k,\, f^k\right)$

Если $k = M$, решить $A^M u^M = f^M$ используя прямой метод.

Иначе:

Применить метод релаксации $S^k$ $\mu_1$ раз к $A^k u^k = f^k$.

Произвести коррекцию на грубой сетке:

Вычислить $r^k = f^k - A^k u^k$.

Вычислить $r^{k+1} = \left(P^k\right)^T r^k$.

Применить $MGV \left(A^{k+1},\, P^{k+1},\, S^{k+1},\, e^{k+1},\, r^{k+1}\right)$.

Обновить решение $u^k = u^k + P^k e^{k+1}$.

Применить метод релаксации $S^k$ $\mu_2$ раз к $A^k u^k = f^k$.

Вышеприведенный алгоритм описывает $V\left(\mu_1,\,\mu_2\right)$ — цикл.

Выбор последовательности сеток и оператора интерполяции являются наиболее важными элементами этапа построения и во многом определяют качество многосеточного метода. Критерием качества являются две измеряемые величины:

• фактор сходимости — показывающий насколько быстро сходится метод, то есть какое количество итераций требуется для достижения заданной точности;
• сложность оператора — определяющей количество операций и объем памяти необходимой для каждой итерации метода.

Сложность оператора $C_{op}$ рассчитывается как отношение количества ненулевых элементов во всех матрицах $A_k,\, k = 1,\,2,\,\dots,\,n$ к количеству ненулевых элементов в матрице первого уровня $A^1 = A$.