Свёрточная нейронная сеть

3D-анимация хода свёртки. Значения в ядре можно извлечь независимо друг от друга. Для периферийных областей входов применяются различные подходы заполнения.

Свёрточная нейронная сеть (англ. convolutional neural network, CNN) — специальная архитектура искусственных нейронных сетей, предложенная Яном Лекуном в 1988 году и нацеленная на эффективное распознавание образов, входит в состав технологий глубокого обучения. Использует некоторые особенности зрительной коры, в которой были открыты так называемые простые клетки, реагирующие на прямые линии под разными углами, и сложные клетки, реакция которых связана с активацией определённого набора простых клеток. Таким образом, идея свёрточных нейронных сетей заключается в чередовании свёрточных слоёв и субдискретизирующих слоёв (слоёв подвыборки). Структура сети — однонаправленная (без обратных связей), принципиально многослойная. Для обучения используются стандартные методы, чаще всего метод обратного распространения ошибки. Функция активации нейронов (передаточная функция) — любая, по выбору исследователя.

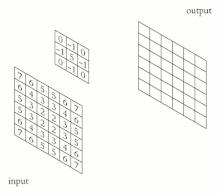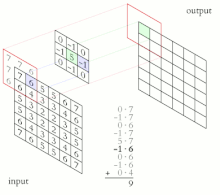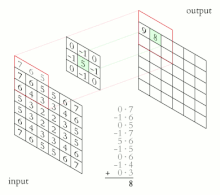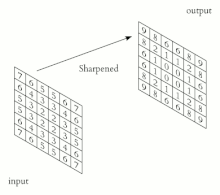
Название архитектура сети получила из-за наличия операции свёртки, суть которой в том, что каждый фрагмент изображения умножается на матрицу (ядро) свёртки поэлементно, а результат суммируется и записывается в аналогичную позицию выходного изображения.

Интерпретация

Работа свёрточной нейронной сети обычно интерпретируется как переход от конкретных особенностей изображения к более абстрактным деталям, и далее к ещё более абстрактным деталям вплоть до выделения понятий высокого уровня. При этом сеть самонастраивается и вырабатывает сама необходимую иерархию абстрактных признаков (последовательности карт признаков), фильтруя маловажные детали и выделяя существенное.

Подобная интерпретация носит скорее метафорический или иллюстративный характер. Фактически «признаки», вырабатываемые сложной сетью, малопонятны и трудны для интерпретации настолько, что на практике суть этих признаков даже не пытаются понять, тем более «подправлять», а вместо этого для улучшения результатов распознавания меняют структуру и архитектуру сети. Так, игнорирование системой каких-то существенных явлений может говорить о том, что либо не хватает данных для обучения, либо структура сети обладает недостатками, и система не может выработать эффективных признаков для данных явлений.

Архитектура и принцип работы

Архитектура свёрточной нейронной сети

Типовая архитектура свёрточной нейронной сети

В обычном перцептроне, который представляет собой полносвязную нейронную сеть, каждый нейрон связан со всеми нейронами предыдущего слоя, причём каждая связь имеет свой персональный весовой коэффициент. В свёрточной нейронной сети в операции свёртки используется лишь ограниченная матрица весов небольшого размера, которую «двигают» по всему обрабатываемому слою (в самом начале — непосредственно по входному изображению), формируя после каждого сдвига сигнал активации для нейрона следующего слоя с аналогичной позицией. То есть для различных нейронов выходного слоя используется одна и та же матрица весов, которую также называют ядром свёртки. Её интерпретируют как графическое кодирование какого-либо признака, например, наличие наклонной линии под определённым углом. Тогда следующий слой, получившийся в результате операции свёртки такой матрицей весов, показывает наличие данного признака в обрабатываемом слое и её координаты, формируя так называемую карту признаков. Естественно, в свёрточной нейронной сети набор весов не один, а целая гамма, кодирующая элементы изображения (например линии и дуги под разными углами). При этом такие ядра свёртки не закладываются исследователем заранее, а формируются самостоятельно путём обучения сети классическим методом обратного распространения ошибки. Проход каждым набором весов формирует свой собственный экземпляр карты признаков, делая нейронную сеть многоканальной (много независимых карт признаков на одном слое). При переборе слоя матрицей весов её передвигают обычно не на полный шаг (размер этой матрицы), а на небольшое расстояние. Так, например, при размерности матрицы весов 5×5 её сдвигают на один или два нейрона (пикселя) вместо пяти, чтобы не «перешагнуть» искомый признак.

Операция субдискретизации (также переводимая как «операция подвыборки» или операция объединения), выполняет уменьшение размерности сформированных карт признаков. В данной архитектуре сети считается, что информация о факте наличия искомого признака важнее точного знания его координат, поэтому из нескольких соседних нейронов карты признаков выбирается максимальный и принимается за один нейрон уплотнённой карты признаков меньшей размерности. За счёт такой операции, помимо ускорения дальнейших вычислений, сеть становится более инвариантной к масштабу входного изображения.

Типовая сеть состоит из большого количества слоёв. После начального слоя (входного изображения) сигнал проходит серию свёрточных слоёв, в которых чередуется свёртка и субдискретизация («пулинг»). Чередование слоёв позволяет составлять «карты признаков», на каждом следующем слое карта уменьшается в размере, но увеличивается количество каналов. На практике это означает способность распознавания сложных иерархий признаков. Обычно после прохождения нескольких слоёв карта признаков вырождается в вектор или даже скаляр, но таких карт признаков возникают сотни. На выходе свёрточных слоёв сети дополнительно устанавливают несколько слоёв полносвязной нейронной сети (перцептрон), на вход которых подаются оконечные карты признаков.

Слой свёртки

Нейроны слоя свёртки, преобразуемые по нескольким выходным каналам

Слой свёртки — это основной блок свёрточной нейронной сети. Слой свёртки включает в себя для каждого канала свой фильтр, ядро свёртки которого обрабатывает предыдущий слой по фрагментам (суммируя результаты поэлементного произведения для каждого фрагмента). Весовые коэффициенты ядра свёртки (небольшой матрицы) неизвестны и устанавливаются в процессе обучения.

Особенностью свёрточного слоя является сравнительно небольшое количество параметров, устанавливаемое при обучении. Так например, если исходное изображение имеет размерность 100×100 пикселей по трём каналам (это значит 30 000 входных нейронов), а свёрточный слой использует фильтры с ядром 3×3 пикселя с выходом на 6 каналов, тогда в процессе обучения определяется только 9 весов ядра, однако по всем сочетаниям каналов, то есть 9×3×6=162, в таком случае данный слой требует нахождения только 162 параметров, что существенно меньше количества искомых параметров полносвязной нейронной сети.

Слой активации

Скалярный результат каждой свёртки попадает на функцию активации, которая представляет собой некую нелинейную функцию. Слой активации обычно логически объединяют со слоем свёртки (считают, что функция активации встроена в слой свёртки). Функция нелинейности может быть любой по выбору исследователя, традиционно для этого использовали функции типа гиперболического тангенса ($f(x)=\tanh(x)$, $f(x)=|\tanh(x)|$) или сигмоиды ($f(x)=(1+e^{-x})^{-1}$). Однако в 2000х годах была предложена и исследована новая функция активации — ReLU (сокращение от англ. rectified linear unit), которая позволила существенно ускорить процесс обучения и одновременно упростить вычисления (за счёт простоты самой функции), что означает блок линейной ректификации, вычисляющий функцию $f(x)=\max(0,x)$. То есть по сути это операция отсечения отрицательной части скалярной величины. По состоянию на 2017 год эта функция и её модификации (Noisy ReLU, Leaky ReLU и другие) являются наиболее часто используемыми функциями активации в глубоких нейросетях, в частности, в свёрточных. Существует методика определения оптимального числа блоков линейной ректификации.

Слой субдискретизации

Субдискретизация с функцией максимума и фильтром 2×2 с шагом 2

Слой субдискретизации (иначе подвыборки или «пулинга») представляет собой нелинейное уплотнение карты признаков, при этом группа пикселей (обычно размера 2×2) уплотняется до одного пикселя, проходя нелинейное преобразование. Наиболее употребительна при этом функция максимума. Преобразования затрагивают непересекающиеся прямоугольники или квадраты, каждый из которых ужимается в один пиксель, при этом выбирается пиксель, имеющий максимальное значение. Операция субдискретизации позволяет существенно уменьшить пространственный объём изображения. Субдискретизация интерпретируется так: если на предыдущей операции свёртки уже были выявлены некоторые признаки, то для дальнейшей обработки настолько подробное изображение уже не нужно, и оно уплотняется до менее подробного. К тому же фильтрация уже ненужных деталей помогает не переобучаться. Слой субдискретизации, как правило, вставляется после слоя свёртки перед слоем следующей свёртки.

Кроме субдискретизации с функцией максимума можно использовать и другие функции — например, среднего значения или L2-нормирования. Однако практика показала преимущества именно субдискретизации с функцией максимума, который включается в типовые системы.

В целях более агрессивного уменьшения размера получаемых представлений, всё чаще находят распространение идеи использования меньших фильтров или полный отказ от слоёв субдискретизации.

Полносвязная нейронная сеть

Основная статья: Перцептрон

После нескольких прохождений свёртки изображения и уплотнения с помощью субдискретизации система перестраивается от конкретной сетки пикселей с высоким разрешением к более абстрактным картам признаков, как правило, на каждом следующем слое увеличивается число каналов и уменьшается размерность изображения в каждом канале. В конце концов, остаётся большой набор каналов, хранящих небольшое число данных (даже один параметр), которые интерпретируются как самые абстрактные понятия, выявленные из исходного изображения.

Эти данные объединяются и передаются на обычную полносвязную нейронную сеть, которая тоже может состоять из нескольких слоёв. При этом полносвязные слои уже утрачивают пространственную структуру пикселей и обладают сравнительно небольшой размерностью (по отношению к количеству пикселей исходного изображения).

Обучение

Наиболее простым и популярным способом обучения является метод обучения с учителем (на маркированных данных) — метод обратного распространения ошибки и его модификации. Но существует также ряд техник обучения свёрточной сети без учителя. Например, фильтры операции свёртки можно обучить отдельно и автономно, подавая на них вырезанные случайным образом кусочки исходных изображений обучающей выборки и применяя для них любой известный алгоритм обучения без учителя (например, автоассоциатор или даже метод k-средних) — такая техника известна под названием patch-based training. Соответственно, следующий слой свёртки сети будет обучаться на кусочках от уже обученного первого слоя сети. Также можно скомбинировать сверточную нейросеть с другими технологиями глубинного обучения. Например, сделать свёрточный авто-ассоциатор, свёрточную версию каскадных ограниченных машин Больцмана, обучающихся за счёт вероятностного математического аппарата, свёрточную версию разреженного кодирования, названную «развертывающими» сетями.

Для улучшения работы сети, повышения её устойчивости и предотвращения переобучения применяется также исключение — метод обучения подсети с выбрасыванием случайных одиночных нейронов.

Преимущества

• Один из лучших алгоритмов по распознаванию и классификации изображений.
• По сравнению с полносвязной нейронной сетью (типа перцептрона) — гораздо меньшее количество настраиваемых весов, так как одно ядро весов используется целиком для всего изображения, вместо того, чтобы делать для каждого пикселя входного изображения свои персональные весовые коэффициенты. Это подталкивает нейросеть при обучении к обобщению демонстрируемой информации, а не попиксельному запоминанию каждой показанной картинки в мириадах весовых коэффициентов, как это делает перцептрон.
• Удобное распараллеливание вычислений, а следовательно, возможность реализации алгоритмов работы и обучения сети на графических процессорах.
• Относительная устойчивость к повороту и сдвигу распознаваемого изображения.
• Обучение при помощи классического метода обратного распространения ошибки.

Недостатки

• Слишком много варьируемых параметров сети; непонятно, для какой задачи и вычислительной мощности какие нужны настройки. Так, к варьируемым параметрам можно отнести: количество слоёв, размерность ядра свёртки для каждого из слоёв, количество ядер для каждого из слоёв, шаг сдвига ядра при обработке слоя, необходимость слоёв субдискретизации, степень уменьшения ими размерности, функция по уменьшению размерности (выбор максимума, среднего и т. п.), передаточная функция нейронов, наличие и параметры выходной полносвязной нейросети на выходе свёрточной. Все эти параметры существенно влияют на результат, но выбираются исследователями эмпирически. Существует несколько выверенных и прекрасно работающих конфигураций сетей, но не хватает рекомендаций, по которым нужно строить сеть для новой задачи.

Ссылки

• Личный сайт Яна Лекуна
• Личный сайт Мэтью Зейлера (M. D. Zeiler)
• Виктор Лемпицкий. Сверточные нейронные сети  (неопр.). ПостНаука (12 августа 2016).