Алгоритм Гровера
Алгоритм Гровера (также GSA от англ. Grover search algorithm) — квантовый алгоритм решения задачи перебора, то есть нахождения решения уравнения
где есть булева функция от n переменных.[1] Был предложен американским математиком Ловом Гровером в 1996 году.
Предполагается, что функция задана в виде чёрного ящика, или оракула, то есть в ходе решения можно задавать оракулу только вопрос типа: «чему равна на данном ?», и использовать ответ в дальнейших вычислениях. То есть, задача решения уравнения (1) является общей формой задачи перебора: здесь требуется отыскать «пароль к устройству », что классически требует полного перебора всех вариантов.
Алгоритм Гровера находит какой-нибудь корень уравнения, используя обращений к функции , с использованием кубитов.[2]
Смысл алгоритма Гровера состоит в «усилении амплитуды» целевого состояния за счёт убывания амплитуды всех других состояний. Геометрически алгоритм Гровера заключается во вращении текущего вектора состояния квантового компьютера по направлению точно к целевому состоянию (движение по наикратчайшему пути обеспечивает оптимальность алгоритма Гровера). Каждый шаг дает вращение на угол , где угол между и составляет . Дальнейшее продолжение итераций оператора G даст продолжение обхода окружности в вещественной плоскости, порождённой данными векторами.
Гроверовское «усиление амплитуды» является, по-видимому, фундаментальным физическим феноменом в квантовой теории многих тел. Например, его учёт необходим для оценки вероятностей событий, которые кажутся «редкими». Процесс, реализующий схему алгоритма Гровера, приводит к взрывному росту первоначально пренебрежимо малой амплитуды, что способно быстро довести её до реально наблюдаемых величин.
Алгоритм Гровера также может быть использован для нахождения медианы и среднего арифметического числового ряда. Кроме того, он может применяться для решения NP-полных задач путём исчерпывающего поиска среди множества возможных решений. Это может повлечь значительный прирост скорости по сравнению с классическими алгоритмами, хотя и не предоставляя «полиномиального решения» в общем виде.
Описание[править | править код]
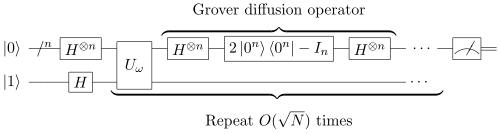
Пусть есть унитарный оператор, зеркально отражающий гильбертово пространство относительно гиперплоскости, перпендикулярной вектору , — состояние, соответствующее корню уравнения (1), — равномерная суперпозиция всех состояний.
Алгоритм Гровера состоит в применении оператора к состоянию число раз, равное целой части . Результат будет почти совпадать с состоянием . Измерив полученное состояние, получаем ответ с вероятностью, близкой к единице.
Замечания[править | править код]
Предположим, уравнение (1) имеет корней. Классический алгоритм решения такой задачи (линейный поиск), очевидно, требует обращений к для того, чтобы решить задачу с вероятностью . Алгоритм Гровера позволяет решить задачу поиска за время , то есть порядка квадратного корня из классического, что является огромным ускорением. Доказано, что Алгоритм Гровера является оптимальным в следующих отношениях:
Алгоритм Гровера есть пример массовой задачи, зависящей от оракула. Для более частных задач удаётся получить большее квантовое ускорение. Например, алгоритм факторизации Шора даёт экспоненциальный выигрыш по сравнению с соответствующими классическими алгоритмами.
То, что f задана в виде чёрного ящика, никак не влияет в общем случае на сложность как квантовых, так и классических алгоритмов. Знание «устройства» функции f (например, знание задающей её схемы из функциональных элементов) в общем случае никак не может помочь в решении уравнения (1). Поиск в базе данных соотносится с обращением функции, которая принимает определённое значение, если аргумент x соответствует искомой записи в базе данных.
Алгоритмы, использующие схему Гровера[править | править код]
- Алгоритм поиска экстремума целочисленной функции (P. Hoyer и др.). Ищется наибольшее значение функции . Квантовый алгоритм находит максимум за обращений к f.
- Алгоритм структурного поиска (Farhi, Gutman). Ищется решение уравнения (1) при дополнительном условии , где разбиение строки на две строки одинаковой длины. Алгоритм имеет сложность порядка квадратного корня из классического времени.
- Алгоритм поиска совпадающих строк в базе данных (Амбайнис). Ищется пара разных аргументов , на которых функция принимает одно и то же значение. Алгоритм требует обращений к f.
Вариации и обобщения[править | править код]
- Непрерывные версии алгоритма Гровера
- Пусть гамильтониан квантовой системы имеет вид , где и представляют собой операторы и соответственно. Тогда непрерывная унитарная эволюция с гамильтонианом , стартуя с , естественно приводит к . Сложность такого непрерывного аналога алгоритма Гровера точно та же, что и для дискретного случая.
- Адиабатический вариант алгоритма Гровера. Медленная эволюция основного состояния типа под действием гамильтониана, зависящего от f, согласно адиабатической теореме, за время порядка ведет к состоянию .
Примечания[править | править код]
- ↑ Иногда GSA неточно называют поиском в базе данных.
- ↑ Сложность работы алгоритма, для задачи с оракулом называемая ещё временем его работы, определяется числом обращений к оракулу.
- ↑ Christof Zalka, Grover’s quantum searching algorithm is optimal, Phys.Rev. A60 (1999) 2746—2751 [1] (недоступная ссылка)
- ↑ Yuri Ozhigov, Lower Bounds of Quantum Search for Extreme Point, Proc.Roy.Soc.Lond. A455 (1999) 2165—2172 [2]
Ссылки[править | править код]
- Гровер Л. К. Квантовая механика помогает найти иголку в стоге сена (для скачивания)
- Логинов О. В. и Цыганов А. В. Квантовый алгоритм Гровера, Санкт-Петербургский Государственный Университет
- Исходные тексты симулятора квантового компьютера на C++ и реализации алгоритма Гровера с подробным описанием и схемами квантовых вентилей

































