Проблема четырёх красок

Проблема четырёх красок

Проблема четырёх красок — математическая задача, предложенная Фрэнсисом Гутри (англ.) в 1852 году, сформулированная следующим образом:

Выяснить, можно ли всякую расположенную на сфере карту раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.

В этой задаче считается что:

1. Граница между любыми двумя областями содержит больше одной точки, то есть возможные стыки произвольного числа областей в одной точке игнорируются.
2. Каждая область является односвязной.

Задача раскраски карты на плоскости эквивалентна задаче на сфере.

Эквивалентные формулировки

В теории графов утверждение теоремы четырёх красок имеет следующие формулировки:

• Хроматическое число плоского графа не превосходит 4.
• Рёбра произвольной триангуляции сферы можно раскрасить в три краски так, что все стороны каждого треугольника были раскрашены в разные цвета.

О доказательстве

Кеннет Аппель^[en] и Вольфганг Хакен^[en] из Иллинойского университета доказали в 1976 году, что так можно раскрасить любую карту. Это была первая крупная математическая теорема, для доказательства которой был применён компьютер. Несмотря на последующие упрощения, доказательство практически невозможно проверить, не используя компьютер. Поэтому некоторые математики отнеслись к этому доказательству с недоверием, что объяснялось не только использованием компьютера, но и громоздкостью описания алгоритма первых доказательств (741 страница); впоследствии были предложены более компактные алгоритмы и скорректирован ряд ошибок. Проблема четырёх красок является одним из известнейших прецедентов неклассического доказательства в современной математике.

История доказательства

Наиболее известные попытки доказательства:

• Альфред Кэмпе предложил доказательство в 1879 году, его опровергли в 1880 году, на основе его идей удалось доказать, что любую карту можно раскрасить в 5 цветов.
• Питер Тэт предложил другое доказательство в 1880 году, его опровергли в 1891 году.
• В своей книге В. А. Горбатов утверждает, что предложил классическое доказательство ещё в 1964 году (объёмом около 30 стр.). Однако опровержений, как и подтверждений, это доказательство пока не получило.

Вариации и обобщения

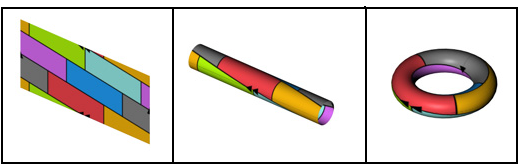
Аналогичные задачи для других поверхностей (тор, бутылка Клейна и т. д.) оказались значительно проще. Для всех замкнутых поверхностей, кроме сферы (и ей эквивалентных плоскости и цилиндра) и бутылки Клейна, необходимое число красок может быть вычислено через эйлерову характеристику $\chi$ по формуле, предложенной в 1890 году Перси Джоном Хивудом (Percy John Heawood) и окончательно доказанной на протяжении 1952—1968 годов группой математиков с наибольшим вкладом Герхарда Рингеля и Теда Янгса (Gerhard Ringel and J. T. W. Youngs)

$p=\left\lfloor\frac{7 + \sqrt{49 - 24 \chi}}{2}\right\rfloor.$

Для бутылки Клейна число равно 6 (а не 7, как по формуле) — это показал П. Франклин в 1934 году, а для сферы — 4.

Для односторонних поверхностей

$p=\left\lfloor\frac{7 + \sqrt{1 + 48g }}{2}\right\rfloor.$.

В старших размерностях разумного обобщения задачи не существует, так как легко придумать уже трёхмерную карту с произвольным числом областей, которые все друг друга касаются.

Игра «четыре краски»

Стивен Барр предложил логическую игру на бумаге для двух игроков, названную «Четыре краски». По словам Мартина Гарднера — «Я не знаю лучшего способа понять трудности, которые встречаются на пути решения проблемы четырёх красок, чем просто поиграть в эту любопытную игру».

Для этой игры нужны четыре цветных карандаша. Первый игрок начинает игру, рисуя произвольную пустую область. Второй игрок закрашивает её любым из четырёх цветов и в свою очередь рисует свою пустую область. Первый игрок закрашивает область второго игрока и добавляет новую область, и так далее — каждый игрок раскрашивает область соперника и добавляет свою. При этом области, имеющие общую границу, должны быть раскрашены в разные цвета. Проигрывает тот, кто на своём ходу вынужден будет взять пятую краску.

Стоит отметить, что в этой игре проигрыш одного из игроков вовсе не является доказательством неверности теоремы (четырех красок оказалось недостаточно!). А лишь иллюстрацией того, что условия игры и теоремы весьма разнятся. Чтобы проверить верность теоремы для полученной в игре карты, нужно проверить связность нарисованных областей и, удалив с неё цвета, выяснить, можно ли обойтись лишь четырьмя цветами для закрашивания получившейся карты (теорема утверждает, что можно).

Существуют также следующие вариации игры:

1. Карта заранее разбивается случайным образом на области различной величины, и каждый ход игры меняется игрок который закрашивает область, а также меняется цвет (в строгой последовательности). Таким образом каждый игрок закрашивает карту только двумя цветами, а в случае если не может закрасить так, чтобы области, имеющие общую границу были раскрашены в разные цвета. пропускает ход. Игра прекращается когда ни один из игроков больше не сможет сделать ни одного хода. Выигрывает тот, у кого общая площадь закрашенных им областей больше.
2. Квадрат разбит на несколько квадратов (в основном 4x4), и его стороны окрашены в один из четырёх цветов (каждый в разный цвет). Первым ходом закрашивается квадрат прилегающий к стороне, каждый последующий ход можно закрашивать тот квадрат, который прилегает к одному из закрашенных квадратов. Нельзя закрашивать квадрат теми цветами, которыми закрашен один из прилегающих к нему квадратов (в том числе и по диагонали) или прилегающая к квадрату сторона. Выигрывает игрок, делающий последний ход.

В культуре

• «Остров пяти красок» — фантастический рассказ Мартина Гарднера.

См. также

• Доказательные вычисления

Литература

• А. А. Зыков. Основы теории графов. — М.: Вузовская книга, 2000. — С. 367—386.
• Р.Курант, Г.Роббинс Что такое математика?
• Самохин А. В. Проблема четырех красок: неоконченная история доказательства // СОЖ. — 2000. — № 7. — С. 91—96.
• Родионов В. В. Методы четырехцветной раскраски вершин плоских графов. — М.: КомКнига, 2000. — 48 с. — 2005 экз. — ISBN 5-484-00127-7
• Thomas, Robin The Four Color Theorem
• Рингель Г. Теорема о раскраске карт / Перевод с английского В. Б. Алексеева. — М.: Мир, 1977. — 256 с. — книга с доказательством проблемы для всех поверхностей, кроме плоскости и сферы