Стирающий код
Стирающий код[1] (англ. erasure code) — в теории кодирования помехоустойчивый код[1], способный восстановить целые пакеты данных в случае их потери[2]. Такой код позволяет бороться с утечками данных при передаче по каналам связи или работе с памятью. Обычно он используется, когда точная позиция потерянных данных известна априори[3].
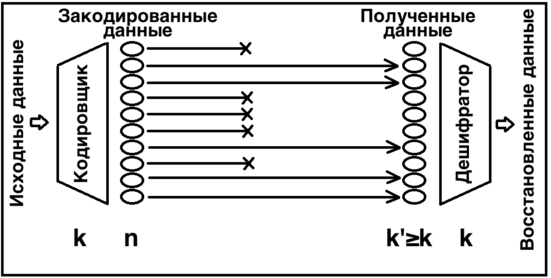
Принцип работы[править | править код]
Стирающий код преобразует сообщение из символов в более длинное сообщение (кодовое слово) из символов так, что исходное сообщение может быть восстановлено по любым символам. Такой код называется кодом, выражение — кодовой долей[4], выражение — эффективностью приёма[5][6].
Стирающий код обычно используется на верхних уровнях стека протоколов каналов передачи и хранения информации[3].
Оптимальный стирающий код[править | править код]
Оптимальный стирающий отличается тем, что любых из символов кодового слова достаточно для восстановления исходного сообщения[7], то есть они имеют оптимальную эффективность приёма[5][8].
Проверка чётности[править | править код]
Рассмотрим случай, когда . С помощью набора из значений вычисляется контрольная сумма и добавляется к исходным значениям:
- .
Теперь в набор из значений включена контрольную сумму. В случае потери одного из значений , его можно будет с лёгкостью восстановить с помощью суммирования оставшихся:
- .
Более сложные комбинации искомых и получаемых значений представляют собой Граф Таннера[4][5].
Линейный код[править | править код]
Важным подклассом стирающего кода является линейный код. Его название связано с тем, что он может быть проанализирован с помощью линейной алгебры. Пусть — исходные данные, — матрица размера , тогда закодированные данные - кода могут быть представлены как . Предположим, что приёмник получил компонент вектора , тогда исходные данные могут быть восстановлены с помощью уравнений, связанных с известными компонентами вектора . Пусть матрица размера соответствует этой системе уравнений. Восстановление возможно, если все эти уравнения линейно независимые и, в общем случае, это означает, что любая матрица размера обратима. Матрица называется генерирующей матрицей кода, так как любой допустимый может быть получен как линейная комбинация столбцов матрицы . Так как её ранг равен , то любое подмножество из закодированных элементов должно содержать информацию о всех исходных данных. Для получения исходных данных необходимо решить линейную систему: , где — подмножество из элементов вектора , доступных на приёмнике[9].
Полиномиальная передискретизация[править | править код]
Пример: Неисправная электронная почта (англ. faulty e-mail)[править | править код]
В случае, когда , избыточные символы могут быть созданы как промежуточные точки на отрезке, соединяющем два исходных символа. Это показано на простом примере, называемом неисправной электронной почтой:

Алиса хочет отправить свой телефонный номер (555629) Бобу, используя неисправную электронную почту. Данный вид почты работает так же, как обычная электронная почта, за следующим исключением:
- Около половины всех сообщений теряются.
- Сообщения длиннее 5 символов запрещены.
- Это очень дорого.
Вместо того, чтобы спросить у Боба подтверждения сообщения, которое она отправила, Алиса придумывает следующую схему:
- Она разбивает свой телефонный номер на две части и отправляет 2 сообщения Бобу — «A=555» и «B=629».
- Она строит линейную функцию , в этом примере . Таким образом и .
- Она считает значения и , а затем отправляет три избыточных сообщения: «C=703», «D=777» и «E=851».
Боб знает, что выражение для следующее , где и — две части телефонного номера. Теперь предположим, что Боб получает «D=777» и «E=851».

Боб может восстановить телефонный номер Алисы с помощью и , используя значения и , которые он получил. Более того, он может это сделать, используя два любых полученных сообщения. Значит, в этом примере кодовая доля равна 40 %. Заметим, что Алиса не может закодировать свой номер телефона только в одном сообщении такой почты, так как он состоит из 6 символов, а максимальная длина одного сообщения — 5 символов. Если бы она отправляла свой номер телефона по частям, запрашивая подтверждения каждой части от Боба, то было бы отправлено минимум 4 сообщения (два от Алисы и два подтверждения от Боба)[5][10].
Общий случай[править | править код]
Приведённая выше линейная конструкция может быть обобщена до полиномиальной интерполяции. В таком случае точки теперь вычисляются над конечным полем , где — число бит в символе. Отправитель нумерует символы данных от до и посылает их. Затем он строит, например, интерполяционный многочлен Лагранжа степени , так что равен -ому символу данных. Потом он отправляет . С помощью полиномиальной интерполяции получатель сможет восстановить потерянные данные в случае, если он успешно принял символов[5].
Реализация в реальном мире[править | править код]
Данный процесс реализован в Коде Рида — Соломона с кодовыми словами, сконструированными над конечным полем при использовании определителя Вандермонда[11].
Почти оптимальный стирающий код[править | править код]
Почти оптимальный стирающий код требует символов, чтобы восстановить сообщение (где ). Величина может быть уменьшена за счёт дополнительного времени работы процессора. При использовании таких кодов необходимо решить, что предпочтительнее: сложность вычислений или возможность коррекции сообщений[11]. В 2004 году существовал только один почти оптимальный стирающий код с линейным временем кодирования и декодирования — код Торнадо[8].
Применение[править | править код]
Стирающие коды применяются в[11]:
- Reliable Multicast (например, в группе по надёжному мультивещанию IETF)
- 3GPP (MBMS и eMBMS (Multimedia Broadcast Multicast Service)
- одноранговых сетях, например, для решения проблемы передачи последнего блока данных
- Распределённых хранилищах.
Примеры[править | править код]
Здесь приведены некоторые примеры различных кодов.
- Почти оптимальные стирающие коды
- Оптимальные стирающие коды
Примечания[править | править код]
- ↑ 1 2 Шинкаренко К. В., Кориков A. M. Помехоустойчивое кодирование мультимедиа данных в компьютерных сетях // Известия Томского политехнического университета [Известия ТПУ] : журнал. — 2008. — 29 сентябрь (т. 313, № 5). — С. 37—41. — ISSN 1684-8519. Архивировано 31 января 2022 года.
- ↑ Шинкаренко Константин Всеволодович, Кориков Анатолий Михайлович. Исследование эффективности помехоустойчивых кодов Лаби // Доклады Томского государственного университета систем управления и радиоэлектроники : журнал. — 2009. — С. 185-192. Архивировано 11 декабря 2019 года.
- ↑ 1 2 Katina Kralevska. Applied Erasure Coding in Networks and Distributed Storage (англ.) // ResearchGate : Thesis for the degree of Philosophiae Doctor. — 2018. — Март. — P. 7. Архивировано 31 января 2022 года.
- ↑ 1 2 J.S. Plank ; A.L. Buchsbaum ; R.L. Collins ; M.G. Thomason. Small parity-check erasure codes - exploration and observations (англ.) // 2005 International Conference on Dependable Systems and Networks (DSN'05) : conference. — 2005. — 25 июль. — P. 2. — ISSN 1530-0889. Архивировано 31 января 2022 года.
- ↑ 1 2 3 4 5 Dave K. Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press, 2012. — С. 377—378. — 512 с. — ISBN 978-1439881811. — ISBN 1439881812.
- ↑ Alexandros G. Dimakis, P. Brighten Godfrey, Martin J. Wainwright and Kannan Ramchandran. Network Coding for Distributed Storage Systems (англ.) // IEEE Transactions on Information Theory : journal. — 2007. — 16 Август (vol. 56, no. 9). — P. 4539—4551. — ISSN 0018-9448. — doi:10.1109/TIT.2010.2054295. Архивировано 31 января 2022 года.
- ↑ N. Alon ; J. Edmonds ; M. Luby. Linear time erasure codes with nearly optimal recovery (англ.) // Proceedings of IEEE 36th Annual Foundations of Computer Science : Symposium. — 1995. — 23-25 Октябрь. — P. 1. — ISSN 0272-5428. — doi:10.1109/SFCS.1995.492581. Архивировано 31 января 2022 года.
- ↑ 1 2 Petar Maymounkov, David Mazi`eres. Rateless Codes And Big Downloads (англ.) // 2nd International Workshop on Peer-to-Peer Systems : conference. — 2004. — Август (vol. 2735). — P. 2. — doi:10.1007/978-3-540-45172-3_23. Архивировано 31 января 2022 года.
- ↑ Luigi Rizzo. Effective Erasure Codes for Reliable Computer Communication Protocols (англ.) // ACM SIGCOMM Computer Communication Review : Newsletter. — 1997. — Апрель (vol. 27, no. 2). — P. 24—36. — doi:10.1145/263876.263881. Архивировано 13 марта 2022 года.
- ↑ Hamid Jafarkhani, Mahdi Hajiaghayi. United States Patent Application Publication. COST-EFFICIENT REPAIR FOR STORAGE SYSTEMS USING PROGRESSIVE ENGAGEMENT 1. The Regents of the University of California,Oakland,CA (US) (22 октября 2015). Дата обращения: 3 декабря 2019. Архивировано 4 мая 2022 года.
- ↑ 1 2 3 Dave K.Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press,, 2012. — С. 380—381. — 512 с. — ISBN 978-1439881811. — ISBN 1439881812.
Литература[править | править код]
- Dave K. Kythe, Prem K. Kythe. Algebraic and Stochastic Coding Theory. — 1-е изд. — CRC Press, 2012. — С. 375—395. — 512 с. — ISBN 978-1439881811.















































