Сумма цифр

График суммы цифр чисел от 0 до 10000

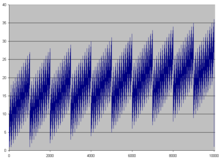
Су́мма цифр в математике — сумма всех цифр натурального числа в конкретной системе счисления. Например, сумма цифр десятичного числа $9045$ равна $9+0+4+5=18$.

Определение

Пусть $n$ — натуральное число. Определим сумму цифр для основания $b>1$ $F_{b}:\mathbb {N} \rightarrow \mathbb {N}$ следующим образом:

$F_{b}(n)=\sum _{i=0}^{k}d_{i}$

где $k=\lfloor \log _{b}{n}\rfloor$ — это количество цифр в этом числе в системе счисления с основанием $b$, и

$d_{i}={\frac {n{\bmod {b^{i+1}}}-n{\bmod {b}}^{i}}{b^{i}}}$ — значение каждой цифры числа.

Например, в системе счисления с основанием 10, сумма цифр числа 84001 равна $F_{10}(84001)=8+4+0+0+1=13$.

Для любых двух оснований $2\leq b_{1}<b_{2}$ и для достаточно больших натуральных чисел $n$,

$\sum _{k=0}^{n}F_{b_{1}}(k)<\sum _{k=0}^{n}F_{b_{2}}(k)$.

Использование

Идея десятичной суммы цифр близко связана, но не совпадает с таким понятием, как цифровой корень — результат повторного применения суммы цифр до того, как оставшееся значение будет числом, состоящим из одной цифры. Цифровой корень всегда является числом от 1 до 9, в то время как сумма цифр может принимать любое значение. Сумма цифр и цифровой корень используются для признаков делимости: натуральное число делится на 3 или 9 тогда и только тогда, когда его сумма цифр (или цифровой корень) делится на 3 или 9 соответственно.

Сумма цифр также часто используется в алгоритмах с контрольной суммой, чтобы проверить работу арифметических операций на ранних компьютерах. Ранее, в эпоху ручных расчётов, Фрэнсис Исидор Эджуорт предложил использовать суммы 50 цифр, взятых из таблиц логарифмов в качестве генерации случайных чисел; если предположить, что каждая цифра случайна, то по центральной предельной теореме эти суммы цифр будут распределены случайно схоже с нормальным распределением.

Сумма цифр числа в двоичной системе счисления известна как вес Хемминга; алгоритмы для произведения этой операции были изучены и включены как встроенные функции в некоторые архитектуры и языки программирования. Эти операции используются в компьютерных программах, в том числе в криптографии, теории кодирования и компьютерных шахматах.

Числа харшад определены как числа, делящиеся на сумму своих цифр, а числа Смита определены равенством между суммой их цифр и суммой цифр их факторизации.

См. также

• Контрольная сумма
• Цифровой корень
• Вес Хемминга
• Числа харшад
• Числа Смита