Трилинейные поляры треугольника

Для термина «Полюс» см. также другие значения.

Для термина «Поляра» см. также другие значения.

Построение трилинейной поляры точки Y

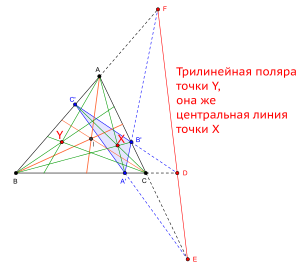
Трилинейные поляры треугольника — некоторые специальные виды прямой линии, связанные с плоскостью треугольника и лежащие в плоскости треугольника. Трилинейная поляра точки Y (полюса) относительно невырожденного треугольника это — прямая линия, определяемая следующим построением. Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной исходной точки (на рис. дано построение трилинейной поляры EDF красной точки Y). Здесь чевианный треугольник — треугольник, тремя вершинами которого являются три основания чевиан исходного треугольника.

Свойства

Трилинейная поляра EDF пересекает три продолжения трех сторон опорного треугольника ABC в трех точках так, что вместе с двумя концами сторон треугольника и с соответствующим основанием одной из трех чевиан образует гармоническую четвёрку точек, лежащих на каждой из трех сторон, включая их продолжения. На рис. справа выше это - три гармонические четвёрки точек: 1) B,C',A,F, 2) B,A',C,D, 3) A,B',C,E.

Примеры трилинейных поляр треугольника

Ось внешних биссектрис или антиортовая ось (antiorthic axis) - трилинейная поляра центра вписанной окружности (инцентра) треугольника ABC)

• Трилинейной полярой центра вписанной окружности (инцентра) служит ось внешних биссектрис или антиортовая ось DEF(antiorthic axis) (см. рис.). На ней лежат все три основания D, E и F трех внешних биссектрис соответственно AD, CE и BF внешних углов треугольника ABC.

Ортоцентрическая ось (Orthic axis) - трилинейная поляра ортоцентра

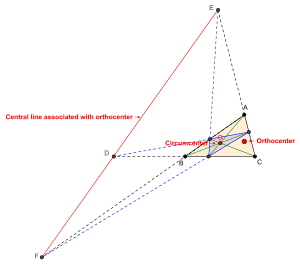
• Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра (см. рис.)

Бесконечно удаленная прямая — трилинейная поляра центроида

Построение трилинейной поляры точки Y

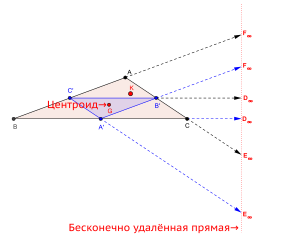
• Бесконечно удаленная прямая — трилинейная поляра центроида (см. рис.)

Ось Лемуана — трилинейная поляра точки Лемуана показана красным цветом

• Трилинейная полярой точки Лемуана служит ось Лемуана (см. рис.)

Трилинейная поляра центра описанной окружности — прямая EDF, показанная красным цветом

• Трилинейная полярой центра описанной окружности служит прямая EDF (см. рис.)

Трилинейная поляра точки Коснита — красная прямая EDF

• Трилинейнай полярой точки Коснита, изогонально сопряженной для центра окружности девяти точек, служит прямая EDF (см. рис.)

• Трилинейные поляры точек, лежащих на описанной конике, пересекаются в одной точке (для описанной окружности это — точка Лемуана, для описанного эллипса Штейнера — центроид)
• Композиция изогонального (или изотомического) сопряжения и трилинейной поляры является преобразованием двойственности. Это означает то, что если точка, изогонально (изотомически) сопряжённая точке $X$, лежит на трилинейной поляре точки $Y$, тогда трилинейная поляра точки, изогонально (изотомически) сопряжённой точке $Y$ лежит на трилинейной поляре точки $X$.

Ортоцентрическая ось — трилинейная поляра ортоцентра показана красным цветом.

Вариации и обобщения

• Существуют также понятие поляры точки P относительно невырожденной кривой второго порядка.
• Трилинейная поляра точки Y, изогонально сопряженной для точки X треугольника, называется центральной линией точки X.

См. также

• Центральная линия (геометрия)
• Полюс и поляра