Глоссарий планиметрии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 августа 2022 года; проверки требуют 328 правок.
Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице).
N[править | править код]
- n-угольник — многоугольник с n вершинами.
А[править | править код]
- Антибиссектриса — чевиана внутри треугольника, изотомически сопряжённая биссектрисе относительно основания медианы, выходящей из той же вершины.
- Антигональное сопряжение — тоже что и антиизогональное сопряжение.
- Антисерединный треугольник (антидополнительный или антикомплементарный) для треугольника образуется проведением через три его вершины трёх прямых, параллельных соответствующим противопложным сторонам, а именно: через вершину прямой параллельно стороне , через вершину прямой параллельно стороне и через вершину прямой параллельно стороне .
- Антимедиатриса отрезка прямой — аналог медиатрисы отрезка, построенный для противоположных сторон выпуклого четырехугольника. В отличие от медиатрисы антимедиатриса — отрезок прямой, также выходящий из середины стороны четырёхугольника, к которой он строится, но он перпендикулярен не к данной стороне четырёхугольника, а к противоположной ей.
- Антипараллелограмм, или контрпараллелограмм, — плоский четырёхугольник, в котором каждые две противоположные стороны равны между собою, но не параллельны, в отличие от параллелограмма. Длинные противоположные стороны пересекаются между собою в точке, находящейся между их концами; пересекаются между собою и продолжения коротких сторон.
- Антипараллель к стороне BC — отрезок B1C1, где точки B1 и C1 лежат на лучах AC и AB, при условии, что ∠AB1C1 = ∠ABC и ∠AC1B1 = ∠ACB. См. также Углы | Между антипараллельными прямыми и их двумя общими секущими.
- Арбелос (по-греч. άρβυλος — сапожный нож) — плоская фигура, образованная большим полукругом, из которого вырезаны два малых полукруга, диаметры которых лежат на диаметре большого полукруга. При этом сумма диаметров двух малых полукругов равна диаметру большого полукруга.
- Асимпто́та кривой γ, имеющей бесконечную ветвь, — прямая, такая, что расстояние от точки γ кривой до этой прямой стремится к нулю при движении её вдоль ветви к бесконечности.
- Аффи́нное преобразование — преобразование плоскости, переводящее прямые в прямые.
Б[править | править код]
- Барице́нтр системы точек Ai с массами mi — точка Z такая что .
- Барицентри́ческие координаты точки X относительно невырожденного треугольника ABC — тройка чисел , такая что и , то есть если разместить в вершины треугольника массы, численно равные , то барицентр полученной системы точек совпадёт с точкой . Барицентрические координаты называют приведёнными, если
- Биссектри́са треугольника, проведённая из вершины — отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противоположной стороне.
- Биссектри́са угла — луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
В[править | править код]
- Вертикальные углы — 2 угла на плоскости, которые образуются при пересечении 2 непараллельных прямых. Эти 2 угла не имеют общих сторон (то есть, стороны одного угла являются продолжением сторон другого).
- Вневпи́санная окружность треугольника — окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон.
- Внеописанный четырёхугольник — это выпуклый четырёхугольник, продолжения всех четырёх сторон которого являются касательными к окружности (вне четырёхугольника). Окружность называется вневписанной. Центр вневписанной окружности лежит на пересечении шести биссектрис.
- Внешний угол — см. многоугольник. См. также Углы.
- Внутренний угол — см. многоугольник. См. также Углы.
- Вписанная окружность треугольника — окружность, касающаяся трёх сторон треугольника.
- Вписанная и вневписанные в треугольник окружности — 4 окружности, каждая из которых касается трёх разных сторон треугольника или их продолжений.
- Впи́санный четырёхуго́льник. Выпуклый четырёхугольник, все вершины которого лежат на одной окружности.
- Высота треугольника. Высотой треугольника называют перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. Иногда так называют длину этого перпендикуляра.
Г[править | править код]
- Геометрическое место точек (ГМТ) — множество точек плоскости, удовлетворяющее определённому условию. Например, серединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от его концов.
- Геометрия треугольника — раздел планиметрии, изучающий свойства треугольника и связанные с ним объекты — центры, прямые и так далее.
- Геронов треугольник — треугольник, стороны и площадь которого являются целыми числами
- Гипербола
- Гипербола — алгебраическая кривая второго порядка.
- Гипербола Енжабека — описанная гипербола, проходящая через ортоцентр и точку Лемуана. На ней лежит центр описанной окружности.
- Гипербола Киперта — кривая, изогонально сопряжённая прямой, проходящей через точку Лемуана и центр описанной окружности данного треугольника.
- Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности. Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха. Изогонально сопряжены друг к другу гипербола Фейербаха и линия центров вписанной и описанной окружностей треугольника.
- Глаз дракона (символ) — старинный символ Древней Германии, обнаруженный Рудольфом Кохом. Глаз дракона похож по внешнему виду на изображение тетраэдра (треугольной пирамиды), если на него смотреть сверху со стороны одной вершины.
- Гомотетия (подобие) с центром O и коэффициентом — преобразование плоскости, переводящее точку P в точку P' , такую что . Гомотетия — частный случай подобия, имеющего неподвижную точку и сохраняющего ориентацию.
Д[править | править код]
- Движение — см. изометрия.
- Дельтоид — напоминающий заглавную букву дельта) — четырёхугольник, четыре стороны которого можно сгруппировать в две пары равных смежных сторон.
- Дельтоид прямоугольный или прямоугольный дельтоид — это дельтоид (четырёхугольник, стороны которого можно сгруппировать в две пары смежных сторон одинаковой длины), который может быть вписан в окружность.
- Дельтоида — (или кривая Штейнера) — плоская алгебраическая кривая, описываемая фиксированной точкой окружности, катящейся по внутренней стороне другой окружности, радиус которой втрое больше радиуса первой.
- Диаметр Брокара — диаметр окружности Брокара.
- Директриса — прямая, лежащая в плоскости конического сечения (эллипса, гиперболы или параболы) и обладающая тем свойством, что отношение расстояния от любой точки кривой до фокуса кривой к расстоянию от той же точки до этой прямой есть величина постоянная, равная эксцентриситету.
- Дополнительные
- Дополнительные углы — это пара углов, которые дополняют друг друга до 90 градусов.
- Дополнительный треугольник — то же самое, что и Серединный треугольник.
Е[править | править код]
- Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.
З[править | править код]
- Задача
- Задача Аполлония — построить с помощью циркуля и линейки окружность, касающуюся трёх данных окружностей. Задача решается с помощью применения двух операций: инверсии и перехода к концентрическим окружностям.
- Задача Наполеона — знаменитая задача построения с помощью циркуля. В этой задаче дана окружность и её центр. Задача состоит в делении окружности на четыре равных дуги с помощью только циркуля.
- Задача о квадратуре круга — задача, заключающаяся в нахождении способа построения с помощью циркуля и линейки (без шкалы с делениями) квадрата, равновеликого по площади данному кругу.
- Задача о трисекции угла — задача о делении заданного угла на три равные части построением циркулем и линейкой.
- Задача упаковки кругов в правильный треугольник в случае упаковки 3 неодинаковых кругов является частным случаем задачи Мальфатти об упаковке 3 неодинаковых кругов в произвольный треугольник.
- Задача Фаньяно — ортотреугольник остроугольного треугольника имеет наименьший периметр среди всех треугольников, вписанных в данный треугольник.
- Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника. Например, замечательными точками треугольника являются точки пересечения:
- Медиан — центроид, центр тяжести (масс);
- Биссектрис — инцентр или центр вписанной окружности;
- Антибиссектрис — центр антибиссектрис;
- Биссектрис внешних углов — центры вневписанных окружностей;
- Высот — ортоцентр;
- Серединных перпендикуляров — центр описанной окружности;
- Симедиан — точка Лемуана
- и многие другие.
- Звезда (геометрия) или Звёздчатый многоугольник.
- «Золотой треугольник» Роберта К. Шона — треугольник с двумя его сторонами, имеющими отношение друг к другу в виде золотого сечения.
И[править | править код]
- Изоме́трия или движение — преобразование подобия с коэффициентом , то есть преобразование плоскости, сохраняющее расстояния.
- Виды изоме́трии или движения: параллельный перенос, вращение, зеркальное отражение, а также их композиции.
- Изогональное сопряжение. Пусть на сторонах BC, CA и AB треугольника ABC взяты точки A1, B1 и C1, причём прямые AA1, BB1 и CC1 пересекаются в одной точке P. Тогда прямые AA2, BB2 и CC2, симметричные этим прямым относительно соответствующих биссектрис, также пересекаются в одной точке Q. В этом случае точки P и Q называются изогонально сопряжёнными относительно треугольника ABC.
- Изогонический центр треугольника. Построим на сторонах треугольника ABC внешним (внутренним) образом правильные треугольники ABC1, AB1C и A1BC. Тогда прямые AA1, BB1 и CC1 пересекаются в одной точке. Эту точку называют первым (вторым) изогоническим центром. Первый изогонический центр называют также точкой Ферма.
- Изодинамический центр треугольника. Пусть AD и AE — биссектрисы внутреннего и внешнего углов треугольника ABC и Sa — окружность с диаметром DE, окружности Sb и Sc определяются аналогично. Тогда эти три окружности имеют две общие точки M и N, которые называются изодинамическими центрами. Кроме того, прямая MN проходит через центр описанной окружности треугольника ABC.
- Изотомическое сопряжение. Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением.
- Изоциркулярное преобразование. Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием. Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция — проективное преобразование, которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.
- Инве́рсия — конформное преобразование, при котором окружности и прямые переходят в прямые и окружности (не обязательно соответственно).
- Инцентр — точка пересечения трёх биссектрис треугольника.
К[править | править код]
- Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны. Квадрат является одновременно частным случаем ромба и прямоугольника.
- Кливер треугольника — это отрезок, один конец которого находится в середине одной из сторон треугольника, второй конец находится на одной из двух оставшихся сторон, при этом кливер разбивает периметр пополам.
- Коллинеа́рные точки. Набор точек, находящихся на одной прямой.
- Коллинеарность векторов (отрезков прямых) означает то, что они лежат на параллельных прямых или на одной прямой.
- Конгруэ́нтные фигуры. Две фигуры называются конгруэнтными, если существует изометрия плоскости, которая переводит одну в другую.
- Конкуре́нтные прямые. Набор прямых, проходящих через одну точку, или попарно параллельных.
- Коника — алгебраическая кривая не выше 2-го порядка, образуемая в результате пересечения конической поверхности с плоскостью. Кониками являются: Гипербола, парабола, эллипс, 2 пересекающихся в 1 точке прямых или 1 прямая, а также 1 точка.
- Коника девяти точек полного четырёхугольника — это коническое сечение, проходящее через три диагональные точки и шесть середин сторон полного четырёхугольника.
- Конфигурация Грюнбаума-Ригби.
- Кривая постоянной ширины a есть замкнутая выпуклая кривая, длина проекции которой на любую прямую равна a.
- Критерий Карно . Пусть дан треугольник АВС и точки А1, В1, С1 на плоскости. Тогда перпендикуляры, опущенные из А1, В1, С1 на BC, АС, AВ соответственно, пересекаются в одной точке тогда и только тогда, когда .
- Круг есть ограниченная часть плоскости, ограниченная окружностью.
- Круговая плоскость. Евклидова плоскость, дополненная одной идеальной точкой ().
Л[править | править код]
- Лемма.
- Лемма Архимеда. Если окружность вписана в сегмент окружности, стягиваемый хордой , и касается дуги в точке , а хорды — в точке , то прямая является биссектрисой угла .

- Лемма Веррьера[1]. Точки касания окружностей Веррьера (полувписанных окружностей) со сторонами лежат на прямой, которая проходит через центр вписанной окружности (инцентр) (См. серый рис. слева).
- Лемма о трезубце или теорема трилистника, или лемма Мансиона (жарг. лемма о куриной лапке) — теорема в геометрии треугольника. В наиболее общем случае теорема гласит, что, если биссектриса к стороне пересекает описанную окружность в точке , то выполняется равенство: , где — инцентр, — центр вневписанной окружности, касающейся стороны .
- Лемма о шестой окружности. Пусть на окружности заданы 4 точки, «А», «B», «C» и «D», и 4 окружности попарно пересекаются в этих точках, а также ещё в 4 других точках W, X, Y и Z. Тогда последние 4 точки лежат на общей окружности.
- Линейка — простейшее средство измерений, как правило представляющий собой узкую пластину, у которой как минимум одна сторона прямая.
- Ломаная (ломаная линия) — геометрическая фигура, состоящая из отрезков, последовательно соединённых своими концами.
- Луч — «полупрямая», имеет начальную точку, но не имеет конечной точки.
М[править | править код]
- Медиа́на треугольника. Отрезок соединяющий вершину треугольника с серединой противоположной стороны.
- Медиатриса. См. Серединный перпендикуляр.
- Многоугольник
- Многоугольник. Замкнутая ломаная на плоскости. Под многоугольником может пониматься, как внешняя его граница в виде замкнутой ломанной (как, например, в случае периметра многоугольника), так и внутренняя плоская фигура, очерченная его внешней границей (как, например, в случае площади многоугольника).
- Многоугольник вписано-описанный — многоугольник, который может быть одновременно описан около некоторой окружности, а также вписан в некоторую окружность. Другое название — двух-окружностный многоугольник.
- Многоугольник вписанный — это выпуклый многоугольник, который содержит описанную окружность.
- Многоугольник выпуклый. Многоугольник называется выпуклым многоугольником, если все его внутренние углы принимают значения не больше 180°.
- Многоугольник вырожденный. Многоугольник называется вырожденным многоугольником, если его внутренний угол хотя бы при одной вершине принимает значение, равное 180° (или равное 0°) или если хотя бы одна из его сторон имеет длину, равную 0 линейных единиц. В случае угла в 0° две его стороны частично или полностью совпадают. В случае угла в 180° две его стороны также совпадают и положение промежуточной (смежной) вершины при этих сторонах становится неопределенным.
- Многоугольник невыпуклый. Многоугольник называется невыпуклым многоугольником, если внутренний угол хотя бы при одной его вершине принимает значение больше 180°.
- Многоугольник описанный, известный также как тангенциальный многоугольник — это выпуклый многоугольник, который содержит вписанную окружность. Это такая окружность, по отношению к которой каждая сторона описанного многоугольника является касательной.
- Многоугольник правильный.
- Мозаика Пенроуза (плитки Пенроуза) — общее название трёх особых типов непериодического разбиения плоскости; названы по имени английского математика Роджера Пенроуза, исследовавшего их в 1970-е годы.
Н[править | править код]
- Накло́нная к прямой ― прямая, пересекающая прямую под углом, отличным от прямого.
- Недезаргова геометрия — проективная геометрия плоскости, в которой теорема Дезарга может не иметь места. В этом случае проективная плоскость называется недезарговой (проективной) плоскостью.
- Неравенство.
- Неравенство Йиффа для угла Брокара : , где — углы искомого треугольника.
- Неравенство Птолемея — неравенство на 6 расстояний между четвёркой точек на плоскости.
- Неравенство Пидо (также неравенство Пидо — Нойберга) — неравенство в геометрии. Неравенство утверждает, что если
, , и , , — длины сторон треугольников и , a и — их площади, тогда
равенство достигается тогда и только тогда, когда эти треугольники подобны с парами соответствующих сторон , и .
- Неравенство треугольника утверждает, что длина любой стороны треугольника всегда меньше суммы длин двух его других сторон: . Обратное неравенство треугольника утверждает, что длина любой стороны треугольника всегда больше модуля разности длин двух его других сторон.
- Неравенство четырёхугольника — модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других сторон: . Эквивалентно: в любом четырёхугольнике (включая вырожденный) сумма длин трёх его сторон не меньше длины четвёртой стороны, то есть: ; ; ; .
О[править | править код]
- Овал
- Овал Декарта — плоская алгебраическая кривая 4-го порядка, представляющая собой геометрическое место точек, для которых сумма расстояний и до двух точек и , называемых фокусами, помноженных на константы и , является постоянной, то есть:

- Овал Кассини — геометрическое место точек M евклидовой плоскости, для которых произведение расстояний до двух данных точек и (называемых фокусами) постоянно и равно квадрату некоторого числа , то есть (см. рис.).
- Окружностно-чевианный треугольник — треугольник с тремя вершинами во вторых точках пересечения с описанной окружностью трёх прямых, проведённых через вершины и данную точку.
- Окру́жность с центром в точке О — геометрическое место точек, равноудалённых от точки О.
- Окру́жность Аполло́ния для данных точек A и B и коэффициента — геометрическое место точек, таких, что .
- Окружность Брокара — описанная окружность треугольника Брокара. Её диаметром является отрезок, соединяющий центр описанной окружности данного треугольника и его точку Лемуана. Две точки Брокара также лежат на этой окружности, как и три вершины треугольника Брокара

- Окружность Веррьера (полувписанные). В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера.
- Окружности Вилларсо — пара окружностей, получаемых при сечении тора вращения «диагональной» касательной плоскостью, проходящей через центр тора (эта плоскость автоматически получается бикасательной).
- Окружность девяти точек — то же, что и Окружность Эйлера
- Окружности Джонсона — набор из трёх окружностей одинакового радиуса r, имеющих одну общую точку пересечения H внутри треугольника, одновременно проходящие через разные пары его вершин. То есть окружности Джонсона являются тремя окружностями, описанными около трёх разных треугольников Гамильтона внутри данного треугольника.

.
- Окружность Конвея. В планиметрии теорема Конвея об окружности утверждает следующее. Пусть стороны, пересекающиеся в каждой вершине треугольника, продолжаются дальше на длину противоположной стороны. Тогда шесть точек, являющиеся свободными концами шести полученных таким образом отрезков (длины трех пар из которых одинаковы), лежат на окружности, центр которой является инцентром треугольника. Окружность, на которой лежат эти шесть точек, называется окружностью Конвея данного треугольника.
- Окружность кривизны или соприкаса́ющаяся окру́жность — окружность, являющаяся наилучшим приближением заданной кривой в окрестности данной точки.
- Окружность Лестера — окружность, на которой в любом разностороннем треугольнике лежат две точки Ферма, центр девяти точек и центр описанной окружности.
- Окружность Ламуна. Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна.
- Окружности Лемуана. Через точку Лемуана данного треугольника проведём прямые, параллельные сторонам этого треугольника. Окружность, проходящая через точки их пересечения со сторонами треугольника (в общем случае таких точек 6), называется первой окружностью Лемуана. Если же через точку Лемуана провести прямые, антипараллельные сторонам треугольника, то окружность, проходящая через точки их пересечения со сторонами треугольника называется второй окружностью Лемуана.
- Окружность Нойберга. Пусть вершины B и C треугольника фиксированы, а вершина A движется так, что угол Брокара треугольника ABC остаётся постоянным. Тогда точка A движется по окружности радиуса , которая и называется окружностью Нойберга.
- Окружность Парри — окружность, проходящая через центроид и две точки Аполлония треугольника, а также через точку Парри.
- Окружности Схоуте. Опустим из точки M перпендикуляры MA1, MB1 и MC1 на прямые BC, CA и AB. Для фиксированного треугольника ABC множество точек M, для которых угол Брокара треугольника A1B1C1 имеет заданное значение, состоит из двух окружностей, причём одна из них расположена внутри описанной окружности треугольника ABC, а другая вне её. Данные окружности называются окружностями Схоуте треугольника .
- Окружность Тейлора треугольника ABC — окружность, которая проходит через шесть точек в виде шести проекций трёх оснований высот треугольника, пересекающих каждую сторону, на две оставшиеся стороны.
- Окружность Тукера (частная окружность Тукера) треугольника ABC — окружность, которая проходит через точки пересечения сторон треугольника ABC с продолжениями сторон треугольника A1B1C1, полученного из треугольника ABC при гомотетии с центром в точке Лемуана. Эти точки (в общем случае их шесть) всегда лежат на одной окружности. Центр окружности Тукера лежит между точкой Лемуана и центром описанной окружности.
- Окружность Тукера (обобщённая окружность Тукера) треугольника ABC. Если на рис. к теореме Томсена справа ниже проводить аналогичную 6-звенную ломаную, последовательно чередуя отрезки параллельные, антипараллельные, параллельные, снова антипараллельные, снова параллельные противоположной текущей стороне и т. д., тогда последний 6-й отрезок вернется в исходную точку, как и в теореме Томсена, и ломаная замкнется. Теорема Тукера утверждает, что в этом случае 6 точек ломаной, лежащих на сторонах треугольника, будут лежать на окружности Тукера
- Окружность Форда (англ. Ford circle) — окружность с центром в точке с координатами и радиусом , где — несократимая дробь.
- Окружность Фурмана — окружность для данного треугольника с диаметром, равным отрезку прямой, который расположен между ортоцентром и точкой Нагеля.
- Окружность Эйлера или окружность девяти точек
- Октаграмма — восьмилучевая звезда, крестострел.
- Ось
- Ось Брокара треугольника ABC является прямой, проходящей через центр описанной окружности треугольника и точку пересечения трех симедиан треугольника ABC.
- Ось внешних биссектрис или антиортовая ось (antiorthic axis) — трилинейная поляра центра вписанной окружности (инцентра) треугольника ABC)
- Ось Лемуана трилинейная поляра точки Лемуана.
- Ось ортоцентрическая (Orthic axis) — трилинейная поляра ортоцентра.
- Описанная окружность многоугольника — окружность, содержащая все вершины многоугольника. Многоугольник, вокруг которого описана окружность, называется вписанным в эту окружность.
- Ортологические треугольники. См. Треугольники ортологические.

- Ортополюс (Orthopole) H системы, состоящей из треугольника ABC и прямой линии ℓ (на рис. она изображена как прямая A ′ C ′) в данной плоскости, является точкой, определяемой следующим образом .
- Ортотреугольник — треугольник, вершинами которого являются основания высот исходного (опорного) треугольника.
- Ортоцентр — точка пересечения трёх высот треугольника.
- Ортоцентрическая система точек. Если в четвёрке точек , , , точка является точкой пересечения высот треугольника , то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек. Другие свойства ортоцентрической системы точек см. в статье ортоцентр.
- Ортоцентроидная окружность неравностороннего треугольника — это окружность, построенная на отрезке, соединяющем его ортоцентр и центроид, как на диаметре.
- Отре́зок — часть прямой между двумя точками, включая концы.
П[править | править код]
- Парабола — геометрическое место точек на плоскости, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
- Парабола Киперта — парабола, вписанная в треугольник, имеющая директрисой прямую Эйлера.
- Парабола, вневписанная для четырёхугольника. Такая парабола существует у любого выпуклого четырёхугольника и она касается всех 4 сторон данного четырёхугольника или их продолжений. Её директриса совпадает с прямой Обера — Штейнера.
- Параллелогра́мм — четырёхугольник, две пары противоположных сторон которого параллельны.
- Параллельные прямые в планиметрии — непересекающиеся прямые.
- Параллельный перенос — преобразование M'=f(M) такое, что все отрезки MM' равны и параллельны. Из этого вытекает, что x' = x + a1, y' = y + a2, где a1,a2 — произвольные константы. Параллельный перенос является изометрией и не имеет неподвижных точек.
- Парке́т или замощение — разбиение плоскости на многоугольники или пространства на многогранники без пробелов и наслоений.
- Педа́льный треугольник см. Подерный треугольник.
- Пентаграмма (пентальфа, пентагерон) или Пифагорейский пентакль — звёздчатый многоугольник, полученный соединением вершин правильного пятиугольника через одну.
- Перпендикулярные прямые на плоскости. Две прямые на плоскости называются перпендикулярными, если при пересечении они образуют 4 прямых угла.
- Перспектор Госсарда. Если брать у треугольника ABC любую пару сторон, а третьей стороной брать первую прямую Эйлера'' треугольника ABC, то перебором трёх вариантов можно построить три треугольника. Их первые прямые Эйлера образуют треугольник AgBgCg, конгруэнтный треугольнику ABC (равный ему, но повёрнутый на некоторый угол). Три пары отрезков, соединяющие сходственные вершины этих двух конгруэнтных треугольников пересекутся в точке Pg, называемой перспектором Госсарда.
- Плоскость Кэли — проективная плоскость над алгеброй Кэли .
- Плоскость Молтона.
- Площадь — некоторая аддитивная неотрицательная величина, сопоставляемая каждой элементарной фигуре.
- Поворот — изометрическое преобразование, являющееся результатом вращения всей плоскости вокруг точки на этой плоскости на заданный угол.
- Поде́рный треугольник точки Р относительно ∆ABC. Треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки Р на стороны треугольника ABC (или их продолжения).
- Подобие — преобразование, сохраняющее отношение расстояний.
- Полиамонд или треуго́льный мо́нстр — геометрическая фигура в виде многоугольника, составленного из нескольких одинаковых равносторонних треугольников, примыкающих друг к другу по рёбрам.
- Полигекс или шестиугольный монстр — геометрическая фигура в виде многоугольника, составленного из нескольких правильных шестиугольников, соединённых сторонами.
- Полимино, или полиомино — плоские геометрические фигуры, образованные путём соединения нескольких одноклеточных квадратов по их сторонам. Это полиформы, сегменты которых являются квадратами.
- Полиформа — плоская или пространственная геометрическая фигура, образованная путём соединения одинаковых ячеек — многоугольников или многогранников. Обычно ячейка представляет собой выпуклый многоугольник, способный замостить плоскость — например, квадрат или правильный треугольник. Некоторые виды полиформ имеют свои названия; например, полиформа, состоящая из равносторонних треугольников — полиамонд.
- Полупериметр многоугольника — полусумма всех его сторон.
- Полюс (полоид) координат ― начало координат в полярной системе координат.
- Полюс (полоид) прямой — образ прямой при полярном преобразовании в инверсии.
- Поляра точки P относительно невырожденной кривой второго порядка — множество точек N, гармонически сопряжённых с точкой P относительно точек M1 и M2 пересечения кривой второго порядка секущими, проходящими через точку P.
- Полюс. Точку P, упомянутую выше, называют полюсом поляры.
- Поризм Понселе — классическая теорема проективной геометрии о множествах многоугольников, вписанных в один эллипс и одновременно описанных около другого.
- Поризм Штейнера о существовании двух цепочек окружностей, каждая из которых последовательно касается двух соседних окружностей внешним образом и двух непересекающихся окружностей (одна из которых лежит внутри другой). Цепочки окружностей напоминают собой цепь Паппа Александрийского.
- Построение с помощью циркуля и линейки — раздел евклидовой геометрии, известный с античных времён.
- Правильный
- Правильный девятиугольник
- Правильный многоугольник — многоугольник, у которого все стороны, а также все внутренние углы равны между собой. Поляра является прямой линией.
- Правильный пятиугольник — правильный многоугольник с пятью равными сторонами и углами.
- Правильный семиугольник — правильный многоугольник с семью равными сторонами и углами.
- Правильный треугольник — то же, что и равносторонний треугольник.
- Правильный четырёхугольник — то же, что и квадрат.
- Преобразование плоскости — взаимнооднозначное отображение плоскости на себя. Часто однако преобразованием называют отображения, которые продолжаются до преобразований расширенной плоскости, например инверсия — преобразование круговой плоскости, перспектива — преобразование проективной плоскости, и т. д.
- Признаки подобия треугольников признаки, позволяющие установить, что два треугольника находятся в отношении подобия.
- Признаки равенства треугольников признаки, позволяющие установить, что два треугольника равны. Подробнее см. раздел «треугольник» подраздел «Признаки равенства треугольников».
- Прилежащие углы — 2 угла на 1 плоскости, имеющие общими по 1 вершине и по 1 из 2 сторон, но не пересекающиеся внутренними областями. Величина угла, образованного 2 внешними (не общими) сторонами прилежащих углов, равна сумме величин самих прилежащих углов.
- Проективная
- Проективная геометрия — раздел геометрии, изучающий проективные плоскости и пространства.
- Проективная плоскость — евклидова плоскость, дополненная идеальной прямой (см. бесконечно удалённая прямая).
- Проективные преобразования — преобразования проективной плоскости, сохраняющие отношение инцидентности.
- Проекция
- Прямая
- Прямая Ньютона — прямая, соединяющая середины диагоналей выпуклого четырёхугольника.
- Прямая Обера — прямая четырёхсторонника, на которой лежат четыре ортоцентра четырёх треугольников, образованных четырьмя попарно пересекающимися прямыми, никакие три из которых не проходят через одну точку. Здесь используются те же четыре треугольника, что и при построении точки Микеля.
прямой Паскаля
- Прямая Паскаля — прямая, упоминаемая в теореме Паскаля, на которой лежат три точки пересечения трёх пар противоположных сторон шестиугольника, вписанного в окружность (или в любое другое коническое сечение — эллипс, параболу, гиперболу или даже в пару прямых).
- Прямая Симсона — прямая, на которой лежат основания перпендикуляров, опущенных из точки описанной окружности треугольника на его стороны или их продолжения.
- Прямая Эйлера — общее название определённого вида прямых треугольника. Например, (первая) прямая Эйлера проходит в треугольнике через: 1) его центроид, 2) ортоцентр, 3) центр его описанной окружности, 4) центр его окружности девяти точек, 5) его точку Экзетера (Exeter point) X(22).
- Прямые.
- Прямой угол — угол в радиан или 90°, половина развёрнутого угла.
- Прямоугольник — четырехугольник, у которого все углы прямые (равны 90 градусам).
- Прямоугольник золотой или золотой прямоугольник — это прямоугольник, длины сторон которого находятся в золотой пропорции, , или (греческая буква фи), где φ примерно равно 1,618.
- Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов).
Р[править | править код]
- Равновеликие фигуры — фигуры, имеющие одинаковую площадь.
- Равные фигуры — фигуры, которые при движении (изометрии) могут быть полностью совмещены друг с другом.
- Равнобедренная трапеция в евклидовой геометрии — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон.
- Равнобедренный треугольник— это треугольник, в котором две стороны равны между собой по длине.


- Радикальная ось двух окружностей — геометрическое место точек, степени которых относительно двух заданных окружностей равны. Иными словами, равны длины четырёх касательных, проведенных к двум данным окружностям из любой точки M данного геометрического места точек.
- Радикальный центр трёх окружностей — точка пересечения трёх радикальных осей пар окружностей. Если радикальный центр лежит вне всех трёх окружностей, то он является центром единственной окружности (радикальной окружности), которая пересекает три данных окружности ортогонально.
- Решение треугольников на плоскости обозначает решение следующей тригонометрической задачи: найти остальные стороны и/или углы треугольника по уже известным. Среди известных элементов треугольника могут быть следующие тройки: 1) три стороны; 2) две стороны и угол между ними; 3) две стороны и угол напротив одной из них; 3) сторона и два прилежащих угла; 4) сторона, противолежащий угол и один из прилежащих. Возможны и другие «неклассические» элементы (биссектрисы, медианы, высоты и др.).
- Ромб — параллелограмм, у которого все стороны равны. Частным случаем ромба является квадрат.
- Ромб золотой или золотой ромб — ромб, чьи диагонали относятся друг к другу как , где (золотое сечение).
- Ромбоид — это параллелограмм, в котором смежные стороны имеют разные длины, и углы не являются прямыми.
С[править | править код]
- Салинон — плоская геометрическая фигура, образованная четырьмя полуокружностями. Впервые исследована Архимедом.
- Серединный, то есть проходящий через середину.
- Серединный перпендикуляр к отрезку прямой (также срединный перпендикуляр или медиатриса) — прямая, перпендикулярная данному отрезку и проходящая через его середину.
- Серединный треугольник — треугольник, образованный средними линиями исходного треугольника.
- Сетка Аполлония — фрактал, строящийся по трём попарно касающимся окружностям.
- Симедиана — отрезок, симметричный медиане треугольника относительно биссектрисы угла этого треугольника. Симедианы треугольника пересекаются в точке Лемуана.
- Симметрия в геометрии. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования. Виды геометрических симметрий: Зеркальная симметрия, Осевая симметрия, Вращательная симметрия, Центральная симметрия, Скользящая симметрия, Винтовая симметрия.
- Скользящая симметрия — композиция симметрии относительно некоторой прямой и переноса на вектор, параллельный этой прямой (этот вектор может быть и нулевым).
- Смежные углы— 2 угла с 1 общей вершиной, 1 из 2 сторон которых — общая, а оставшиеся 2 стороны лежат на 1 прямой (не совпадая). Сумма 2 смежных углов равна 180°. То есть, 2 смежных угла на плоскости это — 2 прилежащих угла, дающих в сумме 180°.
- Сопряжение. В планиметрии сопряжением называется одно из преобразований прямой или точки, порождаемое заданным на плоскости треугольником ABC.
- Сопряжение антигональное. См. Антигональное сопряжение
- Сопряжение изогональное. См. Изогональное сопряжение.
- Сопряжение изотомическое. См. Изотомическое сопряжение.
- Преобразование изоциркулярное . См. Изоциркулярное преобразование. Оно получается, как комбинация изогонального сопряжения и изотомического сопряжения, хотя само сопряжением не является.
- Cопряжённые диаметры. Сопряжёнными диаметрами эллипса (гиперболы) называют пару его (её) диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре. Если эллипс является образом окружности при аффинном преобразовании, то его сопряжённые диаметры являются образами двух перпендикулярных диаметров этой окружности.
- Сопряжённые углы — 2 угла на плоскости, имеющие общими 1 вершину и 2 стороны, по которым они примыкают (граничат) друг к другу, но различаются внутренними областями; объединение таких 2 углов представляет собой всю плоскость, а, как прилежащие углы, они образуют в сумме полный угол; сумма их величин равна 360°.
- Соотношение Бретшнайдера — соотношение в четырёхугольнике, аналог теоремы косинусов.
- Срединный перпендикуляр. См. Серединный перпендикуляр или Медиатрисса.
- Средняя линия.
- Средние линии четырёхугольника. Пусть G, I, H, J — середины сторон выпуклого четырёхугольника ABCD, а E, F — середины его диагоналей. Назовем три отрезка GH, IJ, EF соответственно первой, второй и третьей средними линиями четырёхугольника. Первые две из них также называют бимедианами.
- Средняя линия треугольника или трапеции — отрезок, соединяющий середины боковых сторон. Средняя линия параллельна основанию треугольника (или основаниям трапеции) и равна половине основания треугольника (или полусумме оснований трапеции).
- Степень точки относительно окружности — число , где d — расстояние от точки до центра окружности, a R — радиус окружности.
- Стереографическая проекция — проекция из точки О сферы, проходящей через эту точку на плоскость, касающуюся сферы в точке, антиподальной к точке О.
Т[править | править код]
- Тангенциальный треугольник или касательный треугольник. Если вокруг данного треугольника описать окружность, то треугольник образованный тремя прямыми касательными к окружности проведёнными через вершины , и называется тангенциальным.
- Теорема
- Теорема Аполлония
- Теорема Анне (Anne). В любом четырёхугольнике , не являющемся параллелограммом, прямая Ньютона является геометрическим местом точек , обладающих свойством: , где означает ориентированную площадь .
- Теорема Брахмагупты
- Теорема Брианшона — классическая теорема проективной геометрии.
- Теорема Брокара. Центр описанной около четырёхугольника окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон.
- Теорема Ван-Обеля о треугольнике — классическая теорема аффинной геометрии и геометрии треугольника.
- Теорема Ван-Обеля о четырёхугольнике
- Теорема Вариньона (геометрия) — геометрический факт, доказанный Пьером Вариньоном и утверждающий, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма.
- Теорема Гаусса для квадратов сторон четырёхугольника. Рассмотрим четырехугольник . Пусть , , , , , . Теорема Гаусса утверждает, что .
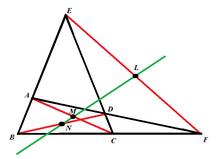
- Теорема Гаусса о серединах диагоналей четырёхугольника. Теорема утверждает, что на одной прямой лежат середины трёх диагоналей полного четырёхугольника. То есть на одной прямой лежат середины двух диагоналей выпуклого четырёхугольника с непараллельными противоположными сторонами, а также середина отрезка, соединяющего две точки пересечения двух пар его противоположных сторон. Она называется прямой Ньютона — Гаусса (зелёная) (см. рис. справа).
- Теорема Вивиани. Для любой точки P внутри равностороннего треугольника сумма перпендикуляров к трем сторонам равна высоте треугольника.
- Теорема Вивиани обобщённая для любой точки P на основании равнобедренного треугольника. Сумма расстояний от произвольной точки, лежащей на основании равнобедренного треугольника, до боковых (равных) сторон есть величина постоянная, равная высоте, опущенной на боковую сторону.
- Теорема Вивиани обобщённая для произвольного треугольника. Если от концов наименьшей из трех сторон треугольника отложить на двух оставшихся сторонах одинаковые отрезки, равные длине наименьшей из трех сторон, то, соединив два невершинных конца отложенных отрезков прямой, получим геометрическое место точек, лежащих внутри треугольника. Для любой точки P этого геометрического места точек внутри треугольника сумма расстояний до трех сторон есть величина постоянная.
- Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
- Теорема Дао о 6 центрах описанных окружностей для вписанного шестиугольника является обощением теоремы Косниты.
- Теорема Дезарга является одной из основных теорем проективной геометрии.
- Теорема Декарта утверждает, что для любых четырёх взаимно касающихся окружностей радиусы окружностей удовлетворяют некоторому квадратному уравнению.
- Теорема Зетеля. Три прямые, соединяющие середины сторон треугольника с серединами соответствующих им чевиан, пересекаются в одной точке. Является обобщением теоремы Шлемильха.
- Теорема Кейси.
- Теорема косинусов.
- Теорема косинусов для четырёхугольника.
- Теорема Косниты.
- Теорема котангенсов.
- Теорема Лейбница (геометрия).
- Теорема Лестера. В любом разностороннем треугольнике две точки Торричелли, центр девяти точек и центр описанной окружности лежат на одной окружности — на (окружности Лестера).
- Теорема Мавло. Треугольник на своей окружности девяти точек отсекает внешним образом тремя своими сторонами три дуги таким образом, что длина наибольшей из них равна сумме длин двух оставшихся дуг.
- Теорема Максвелла (геометрия).
- Теорема Массельмана.
- Теорема Менелая или теорема о трансверсалях, или теорема о полном четырёхстороннике, — классическая теорема аффинной геометрии.
- Теорема Микеля.
- Теорема Микеля-Штейнера о четырёхстороннике. Пусть 4 прямые расположены так (в общем положении), что при их пересечении образуется 4 треугольника. Фигура напоминает собой выпуклый четырёхугольник (не трапецию), в котором продолжены до их пересечения 2 пары противоположных сторон. Тогда описанные вокруг этих треугольников окружности имеют общую точку, которая называется точкой Микеля этой конфигурации прямых.
- Теорема Монжа о трёх окружностях. Для трёх произвольных окружностей, каждая из которых не лежит целиком внутри другой, три точки пересечения общих внешних касательных к каждой паре окружностей лежат на одной прямой.
- Теорема Монжа об ортоцентре вписанного четырёхугольника. 4 отрезка прямых (4 антимедатрисы), проведенных из середин 4 сторон вписанного четырёхугольника перпендикулярно к противолежащим сторонам, пересекаются в ортоцентре Н этого четырёхугольника.
- Теорема Морли о трисектрисах.
- Теорема Наполеона — утверждение евклидовой планиметрии о равносторонних треугольниках: Если на каждой стороне произвольного треугольника построить по равностороннему треугольнику, то треугольник с вершинами в центрах равносторонних треугольников — тоже равносторонний.
- Теорема Ньютона (планиметрия) — теорема о том, что прямая Ньютона описанного четырёхугольника проходит через центр его вписанной окружности.
- Теорема о бабочке.
- Теорема о биссектрисе.
- Теорема о внешнем угле треугольника.
- Теорема о вписанных окружностях.
- Теорема о двух секущих
- Теорема о дележе пиццы.
- Теорема о проекциях.
- Теорема о пяти окружностях.
- Теорема о равнобедренном треугольнике.
- Теорема о семи окружностях. Проведём цепочку из шести внутренних окружностей, каждая из которых касается двух соседних окружностей внешним образом и седьмой большой (общей для всех шести) окружности внутренним образом. Тогда три линии, проведенные между противоположными парами точек касания трех пар из шести окружностей с седьмой окружностью, пересекаются в одной точке.
- Теорема о сумме углов многоугольника.
- Теорема о сумме углов треугольника.
- Теорема о шести окружностях.
- Теорема Паппа о невыпуклом шестиугольнике, касающемся 2 прямых, — классическая теорема проективной геометрии. Она является вырожденным случаем в теореме Паскаля.
- Теорема Паппа о площадях.
- Теорема о произведении отрезков хорд.
- Теорема Паскаля — классическая теорема проективной геометрии.
- Теорема Пито утверждает, что у описанного четырёхугольника (то есть четырёхугольника, в который можно вписать окружность) суммы длин противоположных сторон равны.
- Теорема Пифагора. В любом плоском прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- Теорема Помпею.
- Теоремы Птолемея. Для простого (несамопересекающегося) четырёхугольника, вписанного в окружность, имеющего длины пар противоположных сторон: a и c, b и d, а также длины диагоналей e и f, справедливы первая и вторая теоремы Птолемея: ;
- Теорема Ригби. Если к любой стороне остроугольного треугольника провести высоту и касающуюся её с другой стороны вневписанную окружность, то точка касания последней с этой стороной, середина упомянутой высоты, а также инцентр лежат на одной прямой. Из теоремы Ригби следует, что 3 отрезка, соединяющих середину каждой из 3 высот треугольника с точкой касания вневписанной окружности, проведенной к той же стороне, что и высота, пересекаются в инцентре.
- Теорема Ройшле.

- Теорема Сальмона о трёх коллинеарных точках (см. рис.). Если через (синюю на рисунке) точку окружности проведены три произвольные хорды (вторые концы которых на рисунке зелёного цвета), на которых как на диаметрах построены три окружности, то эти три окружности попарно пересекаются вторично в трёх коллинеарных точках (они на рисунке красного цвета).
- Теорема Сальмона о гармоническом делении отрезка HO . Расстояния между ортоцентром H треугольника и его центром тяжести G делится гармонически центром описанного круга O и центром окружности Эйлера O9.
- Теорема синусов.
- Теорема Стюарта.
- Теорема Сунса об ортополюсе. Если в данной плоскости для 3 вершин фиксированного треугольника ABC построить их проекции на произвольную фиксированную прямую ℓ в виде 3 точек (в виде проекций 3 вершин треугольника), а затем спроектировать обратно эти 3 полученные точки-проекции на прямой ℓ на 3 стороны треугольника ABC, причем проекцию каждой точки (проекцию каждой вершины) проектировать лучом на противоположную этой вершине сторону треугольника ABC, тогда 3 последних проектирующих луча или их продолжения пересекутся в одной точке, называемой ортополюсом[2].
- Теорема тангенсов.
- Теорема Тебо.
- Теорема Томсена.
- Теорема Уркхарта. Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F, то для того, чтобы этот четырёхугольник был внеописанным для окружности, необходимо и достаточно, чтобы выполнялось любое из двух условий:
- Теорема Фалеса о пропорциональных отрезках — теорема планиметрии о наборе параллельных секущих к паре прямых.
- Теорема Фалеса об угле, опирающемся на диаметр окружности — классическая теорема планиметрии, частный случай теоремы о вписанном угле.
- Теорема Фейербаха.
- Теорема Фусса связывает расстояние между центрами описанной и вписанной окружностей (радиусы и ) вписанно-описанного четырёхугольника и их радиусы
- Теорема Харкорта.
- Теорема Хузеля уточнённая (Housel). Центр тяжести (G) данного треугольника ABC (центроид), центр вписанной окружности (I), его точка Нагеля (M) и центр (S) круга, вписанного в дополнительный треугольник A’B’C (или в Центр Шпикера), лежат на одной прямой. Более того,
- Теорема Чевы — классическая теорема аффинной геометрии и геометрии треугольника. Установлена в 1678 году итальянским инженером Джованни Чевой.
- Теорема Шиффлера. Если в треугольнике ABC с центром вписанной окружности I рассмотреть три треугольника BCI, CAI и ABI, то их три (первые) прямые Эйлера, а также (первая) прямая Эйлера треугольника ABC (все четыре прямые) пересекутся в одной точке — в точке Шиффлера Sp.
- Теорема Шлёмильха. Три прямые, соединяющие середины сторон треугольника с серединами его соответствующих высот, пересекаются в одной точке.
- Теорема Штейнера об изогонально сопряженных отрезках, проведенных из одной вершины треугольнмка — классическая теорема геометрии треугольника, обобщение теоремы о биссектрисе.
- Теорема Штейнера — Лемуса — теорема геометрии треугольника. Если в треугольнике равны 2 биссектрисы, то этот треугольник является равнобедренным.
- Теорема Штейнера — Понселе — теорема из области геометрических построений, утверждающая, что любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
- Теорема Штейнера об ортологических треугольниках утверждает, что, если перпендикуляры, опущенные из вершин одного ортологического треугольника на соответствующие стороны другого ортологического треугольника, пересекаются в одной точке (в отрологическом центре первого ортологического треугольника), то и перпендикуляры, опущенные из вершин второго ортологического треугольника на соответствующие стороны первого ортологического треугольника, также пересекаются в одной точке (в отрологическом центре второго ортологического треугольника).
- Теорема Эйлера о треугольнике. См. Формула Эйлера для треугольника.
- Теорема Эйлера о четырёхугольниках. См. Формула Эйлера для четырёхугольника.
- Тождество параллелограмма — сумма квадратов длин сторон параллелограмма равна сумме квадратов длин его диагоналей: .
- Точка. См. также Точки.
- Точка Аполлония — специальная точка в треугольнике. Определяется как точка пересечения прямых, соединяющих вершины треугольника с точками касания 3 вневписанных окружностей треугольника с описанной вокруг них окружностью.
- Точка Бевэна является центром окружности, проходящей через центры вневписанных окружностей.
- Точка Брокара — специальная точка в треугольнике. Если соединить точку Брокара с вершинами треугольника, тогда три отдельных полученных отрезка будут видны из вершин треугольника под одинаковым углом (под углом Брокара), смотря последовательно каждый раз на один из каждой пары, пропуская другой (только четный или только нечетный).
- Точка Веррьера. В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера. Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную.
- Точка Жергонна — точка пересечения чевиан, проходящих через точки касания вписанной окружности со сторонами этого треугольника. Точка Жергонна изотомически сопряжена точке Нагеля.
- Точка Косниты — является изогонально сопряжённой центру девяти точек.
- Точка Лоншана — точка зеркального отражения ортоцентра треугольника ABC относительно его центра описанной окружности (L= de Longchamps point=перевод не по правилам), введённую французским математиком Gaston Albert Gohierre. Эта точка — ортоцентр антидополнительного треугольника.
- Точка Микеля. Пусть четыре прямые расположены так (в общем положении), что при их пересечении образуется четыре треугольника (см. рис.). Тогда описанные вокруг этих треугольников окружности имеют общую точку, которая называется точкой Микеля этой конфигурации прямых
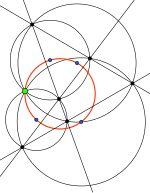
Точка Микеля - Точка На́геля — точка пересечения прямых, соединяющих вершины треугольника с точками касания противоположных сторон с вневписанными окружностями. Точка Нагеля изотомически сопряжена точке Жергонна.
- Точка Понселе — точка, образованная на пересечении четырёх окружностей девяти точек треугольников , , и , если эта четверка точек не образует ортоцентрическую систему.
- Точка Парри. Окружность Парри и описанная окружность треугольника ABC пересекаются в двух точках. Одна из них — фокус параболы Киперта треугольника ABC. Другая точка пересечения называется точкой Парри треугольника ABC.
- Точка слабая в треугольнике (weak point) — точка, у которой может найтись близнец с помощью её ортогонального сопряжения за пределы треугольника. Например, инцентр, точка Нагеля и другие являются слабыми точками, ибо допускают получение аналогичных точек при их сопряжении за пределы треугольника.
- Точка Тарри
- Точка Торричелли — точка, из которой все стороны видны под углом 120°. Эту точку также называют изогонической (равноугольной) точкой.
- Точка Фейербаха
- Точка Ферма
- Точка Шиффлера
- Точка Штейнера
- Точка эксетерская. См. Эксетерская точка.
- Точки
- Точки Адзимы — Мальфатти. Пусть дан треугольник ABC и его три окружности Мальфатти, пусть D, E и F — точки, где две окружности касаются, противоположные вершинам A, B и C соответственно. Тогда три прямые AD, BE и CF пересекаются в одной замечательной точке, известной как первая точка Адзимы — Мальфатти. Вторая точка Адзимы — Мальфатти — точка пересечения трёх прямых, соединяющих точки касания окружностей Мальфатти с центрами вневписанных окружностей треугольника.
- Точка Аполлония — точка, образованная пересечением трёх перпендикуляров проведённых от сторон треугольника так, что педальный треугольник, вершины которого — основания перпендикуляров, является равносторонним. Эту точку также называют изодинамической точкой. Их две.
- Точки Брокара — такие внутренние точки P и Q , что и .
- Точки Вектена
- Точки изотомически сопряжённые Пусть прямые и пересекают прямые и в точках и соответственно, а точки и выбраны на прямых и так, что , и . Тогда прямые и либо параллельны, либо также пересекаются в одной точке . В последнем случае точки и называют изотомически сопряжёнными относительно треугольника .
- Точки Наполеона
- Точки постоянные подобных фигур Пусть , и — соответственные прямые подобных фигур , и , пересекающиеся в точке . Пусть , и — точки пересечения прямых , и с окружностью подобия, отличные от точки . Оказывается, что эти точки зависят только от фигур , и и не зависят от выбора прямых , и . Точки , и и называют постоянными точками подобных фигур , и , а треугольник называют постоянным треугольником подобных фигур , и .
- Точки соответственные. Точки и называют соответственными точками подобных фигур и , если при поворотной гомотетии, переводящей в , точка переходит в . Аналогично определяются соответственные прямые и отрезки.
- Точки Ригби — внутренние и внешние точки в теореме Ригби.
- Точки Торричелли
- Точки Фейербаха — точки попарного касания вписанной и трёх вневписанных окружностей с окружностью девяти точек.
- Трактриса (линия влечения) — (от лат. trahere — тащить) — плоская трансцендентная кривая, для которой длина отрезка касательной от точки касания до точки пересечения с фиксированной прямой является постоянной величиной.
- Трапеция — выпуклый четырёхугольник, у которого две стороны параллельны. Часто в определение трапеции добавляют условие, что две другие стороны должны быть не параллельны.
- Транспортир — инструмент для построения и измерения углов.
- Треугольник.
- Треугольник Брокара — треугольник с вершинами в постоянных точках треугольника. Треугольник Брокара вписан в окружность Брокара.
- Треугольники Гамильтона — треугольники, фигурирующие в теореме Гамильтона. Три треугольника Гамильтона это — те три треугольника, на которые разбивают данный остроугольный треугольник три отрезка прямых, соединяющих ортоцентр с тремя его вершинами.
- Треугольник геронов. См. Геронов треугольник.
- Треугольник египетский. См. Египетский треугольник.
- Треугольник Жергонна для основного треугольника ABC определяется тремя точками касания вписанной окружности трёх его сторон.
- Треугольник золотой. См. Золотой треугольник (геометрия).
- Треугольник Кеплера — это прямоугольный треугольник, длины сторон которого составляют геометрическую прогрессию. При этом соотношение длин сторон треугольника Кеплера связано с золотым сечением .
- Треугольник Наполеона для треугольника — равносторонний треугольник, образованный центрами равносторонних треугольников, построенных на всех сторонах данного треугольника.
- Треугольник подобия. Пусть , и — три подобные фигуры, — центр поворотной гомотетии, переводящей в , точки и определяются аналогично. Если точки , и не лежат на одной прямой, то треугольник называют треугольником подобия фигур , и , а его описанную окружность называют окружностью подобия этих фигур. В случае, когда точки , и совпадают, окружность подобия вырождается в центр подобия, а в случае, когда эти точки не совпадают, но лежат на одной прямой, окружность подобия вырождается в ось подобия
- Треугольник постоянный См. точки постоянные подобных фигур.
- Треугольник равнобедренный.
- Треугольник Рёло
- Треугольник ортоцентрический. См. Ортотреугольник.
- Треугольник отражений. Вершины треугольника отражений получаются зеркальным отражением каждой вершины опорного треугольника относительно противоположной стороны.
- Треугольник подерный. См. Подерный треугольник.
- Треугольник правильный или равносторонний треугольник. См. Правильный треугольник.
- Треугольник прямоугольный. См. Прямоугольный треугольник.
- Треугольник равнобедренный. См. Равнобедренный треугольник.
- Треугольник равнобедренный прямоугольный. См. Равнобедренный прямоугольный треугольник.
- Треугольник серединный или срединный треугольник, или дополнительный треугольник. См. Серединный треугольник
- Треугольник тангенциальный или касательный треугольник. См. Тангенциальный треугольник.
- Треугольник точек касания вневписанных окружностей. Этот треугольник иногда называют треугольником Нагеля.
- Треугольник трёх внешних биссектрис (треугольник центров вневписанных окружностей) — треугольник, образованный точками пересечения внешних биссектрис друг с другом в центрах вневписанных окружностей исходного треугольника (см. рис.)

Треугольник трёх внешних биссектрис - Треугольник чевианный. См. Чевианный треугольник.
- Треугольник целочисленный. См. Целочисленный треугольник.
- Треугольник Шарыгина — треугольник, не являющийся равнобедренным, основания биссектрис которого образуют равнобедренный треугольник.
- Треугольник Эйлера-Фейербаха — треугольник, три вершины которого являются серединами отрезков, соединяющих с ортоцентром вершины исходного треугольника.
- Треугольники.
- Треугольники ортологические — треугольники ABC и A1B1C1, для которых перпендикуляры, опущенные из точек A, B и C на прямые B1C1, C1A1 и A1B1 пересекаются в одной точке (называемой первым центром ортологии). В этом случае и перпендикуляры, опущенные из точек A1, B1 и C1 на прямые BC, CA и AB также пересекаются в одной точке (называемой вторым центром ортологии). Треугольники ортологические связаны между собой с помощью теоремы Штейнера об ортологических треугольниках.
- Треугольники подобные — два треугольника на евклидовой плоскости, углы у которых соответственно равны, а стороны соответственно пропорциональны. Такие треугольники являются подобными фигурами.
- Треугольники равные (с точностью до конгруэнтности) — два треугольника на евклидовой плоскости, у которых равны любые из следующих троек основных соответствующих элементов (равны соответствующие стороны и углы у одного и у другого треугольника): 1) , , (равенство по двум сторонам и углу между ними); 2) , , (равенство по стороне и двум прилежащим углам); 3) , , (равенство по трём сторонам). Такие треугольники являются равными фигурами.
- Трилинейные поляры треугольника. Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной полярой исходной точки.
- Трисектри́са
- Трисектри́са угла есть луч, делящий этот угол в отношении 2:1.
- Трисектри́са — плоская кривая.
- Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой.
- Тупой угол — угол, величина которого находится между 90 и 180 градусами.
У[править | править код]
- Угол.
- Угол Брокара. Пусть P — точка Брокара треугольника ABC. Угол = ∠ABP = ∠BCP = ∠CAP называется углом Брокара этого треугольника.
- Угол, вписанный в окружность — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
- Угол косой — любой угол, не равный 0°, 90°, 180° или 270°.
- Угол между окружностями — угол между касательными к окружностям в точке пересечения этих окружностей. Оба угла между двумя пересекающимися окружностями равны.
- Угол между окружностью и прямой — угол между прямой и касательной к окружности в точке пересечения прямой и окружности. Оба угла между пересекающимися окружностью и прямой равны.
- Угол нулевой — угол, равный 0°; стороны нулевого угла совпадают, его внутренняя область — пустое множество.
- Угол, опирающийся на диаметр окружности, вписанный в эту окружность, является прямым углом (в 90 градусов).
- Угол острый — угол меньший, чем 90°, но больший, чем 0°.
- Угол полный — угол, равный 360°; включает в себя всё множество точек плоскости; см. оборот (единица измерения).
- Угол полный численно равен двум развёрнутым углам или четырёмпрямым углам.
- Угол прямой — угол, равный 90° или четверти полного угла . 2 стороны прямого угла перпендикулярны друг другу.
- Угол развёрнутый — угол, равный 180° или половине полного угла . Сторонами развёрнутого угла являются две полупрямые одной прямой, то есть два луча, направленных в противоположные стороны.
- Угол тупой — угол больший, чем 90°, но меньший, чем 360°.
- Угол центральный — угол с вершиной в центре окружности, сторонами которого являются 2 радиуса этой окружности вместе с их продолжениями за её пределы.
- Углы.
- Между пересекающимися прямыми.
- Вертикальные. См. Вертикальные углы.
- Дополнительные. См. Дополнительные углы.
- Прилежащие. См. Прилежащие углы.
- Смежные. См. Смежные углы.
- Сопряжённые. См. Сопряжённые углы.
- Между параллельными прямыми и их общей секущей.
- Соответственные углы равны, .
- Внутренние (внешние) накрест лежащие углы равны, .
- Внутренние (внешние) односторонние углы являются дополнительными, .
- Между антипараллельными прямыми и их двумя общими секущими.
- Две антипараллельные прямые и их две общие секущие образуют выпуклый невырожденный четырёхугольник, в котором пара противоположных внутренних (внешних) углов является двумя дополнительными углами, .
- Углы у многоугольников (у треугольников).
- Внутренний угол при данной вершине многоугольника (треугольника) образован двумя сторонами, выходящими из данной вершины.
- Все внутренние углы у выпуклого многоугольника принимают значения между 0° и 180° не включительно.
- Если внутренний угол хотя бы при одной вершине многоугольника принимает значение, равное 180° (или равное 0°), то он называется вырожденным многоугольником.
- Если внутренний угол хотя бы при одной вершине многоугольника принимает значение больше 180°, то он называется невыпуклым многоугольником.
- Если внутренний угол хотя бы при одной вершине треугольника принимает значение, равное 90° (большее 90°), то он называется прямоугольным (тупоугольным) треугольником. В противном случае он называется остроугольным треугольником.
- Внешний угол многоугольника (треугольника) образован одной стороной, выходящей из данной вершины, и продолжением другой стороны, выходящей из той же вершины.
- Внешний угол многоугольника (треугольника) равен разности между 180° и его внутренним, смежным с ним, углом. Для выпуклого (невырожденного) многоугольника (треугольника) внешний угол может принимать значения от 0 до 180° не включительно. Для невыпуклого (невырожденного) многоугольника (но не треугольника) он может принимать значения от 180° до 360° не включительно.
Ф[править | править код]
- Формула
- Формула Брахмагупты — выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон.
- Формула Герона — — формула для вычисления площади треугольника по длинам его сторон : : , где — полупериметр треугольника: .
- Формула Карно — теорема геометрии треугольника, которая связывает сумму расстояний от произвольной точки плоскости до 3 сторон треугольника и радиусы его вписанной и описанной окружностей.
- Формула Парамешвары. Для вписанного четырёхугольника со сторонами a, b, c, d (в указанной последовательности) и полупериметром p радиус описанной окружности задаётся формулой:
- Формула площади Гаусса.
- Формулы Мольвейде — тригонометрические зависимости, выражающие отношения между длинами сторон и значениями углов при вершинах некоторого треугольника.
- Формула Эйлера для треугольника — формула для квадрата расстояния между центрами описанной и вписанной окружностей и их радиусами и соответственно:
- Формула Эйлера для четырёхугольника: учетверённый квадрат расстояния между серединами диагоналей () равен сумме квадратов четырёх сторон четырёхугольника минус сумма квадратов двух его диагоналей. Для четырёхугольника ABCD она имеет вид: .
- Фигура — произвольное подмножество плоскости.
Х[править | править код]
- Хо́рда кривой — отрезок, концы которого лежат на данной кривой.
Ц[править | править код]
- Цветок жизни — геометрическая фигура, образованная пересечением равномерно размещённых окружностей с одинаковым радиусом. Окружности расположены так, что образуют симметричный шестилучевой узор, элемент которого похож на цветок с шестью лепестками.
- Центр
- Центр вписанной окружности
- Центр масс. См. Барицентр, Центроид треугольника.
- Центр масс периметра треугольника известен под названием «центр Шпикера».
- Центр окружности.
- Центр окружности девяти точек
- Центр симметрии
- Центр фигуры
- Центр Шпикера
- Центральная симме́три́я Центра́льной симме́три́ей относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA, в то время как обозначение SA можно перепутать с осевой симметрией. Это преобразование эквивалентно повороту на 180° относительно точки А.
- Центральные прямые — это некоторые специальные прямые, связанные с треугольником и лежащие в плоскости треугольника. Особое свойство, которое отличает прямые как центральные прямые, проявляется через уравнение прямой в трилинейных координатах.
- Центро́ид
- Центроид треугольника треугольника — точка пересечения медиан треугольника.
- Цепь Паппа Александрийского — кольцо внутри двух касающихся кругов, заполненных попарно касающимися кругами меньших диаметров.
- Цепь Понселе: Пусть и — два конических сечения. Ломаная называется цепью Понселе для пары , , если каждая вершина лежит на , и при этом (продолжения) рёбер и являются соответственно правой и левой касательной к .
- Циркуль — инструмент для черчения окружностей и дуг, также для измерения расстояний, в частности, на картах.
Ч[править | править код]
- Чевиана — отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой на противоположной ей стороне или на её продолжении. Обычно под чевианой понимают не один такой отрезок, а один из трёх таких отрезков, проведённых из трёх разных вершин треугольника и пересекающихся в одной точке. Они удовлетворяют условиям теоремы Чевы.
- Чевианный треугольник — треугольник, тремя вершинами которого являются три основания чевиан исходного треугольника.
- Четырёхсторонник — в планиметрии то же, что и четырёхугольник.
- Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники, невыпуклый четырёхугольник может быть самопересекающимся.
- Четырёхугольник внеописанный или внеописанный четырёхугольник — это выпуклый четырёхугольник, продолжения всех четырёх сторон которого являются касательными к окружности (вне четырёхугольника).
- Четырёхугольник, вписанный в окружность или вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности.
- Четырёхугольник вписанно-описанный или вписанно-описанный четырёхугольник — это выпуклый четырёхугольник, который имеет как вписанную окружность, так и описанную окружность.
- Четырёхугольник Ламберта — это четырёхугольник, имеющий при трёх его вершинах прямые углы.
- Четырёхугольник описанный или описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника.
- Четырёхугольник ортодиагональный или ортодиагональный четырёхугольник — это четырёхугольник, в котором диагонали пересекаются под прямым углом.
- Четырёхугольник полный или полный четырёхугольник (иногда употребляется термин полный четырёхвершинник) — это система геометрических объектов, состоящая из любых четырёх точек на плоскости, никакие три из которых не лежат на одной прямой, и шести прямых, соединяющих шесть пар точек.
- Четырёхугольник равнодиагональныйили равнодиагональный четырёхугольник — это выпуклый четырёхугольник, две диагонали которого имеют равные длины.
- Четырёхугольник Саккери — это четырёхугольник с двумя равными сторонами, перпендикулярными основанию.
Э[править | править код]
- Эксетерская точка
- Эллипс — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек и (называемых фокусами) постоянна и больше расстояния между фокусами, то есть: причём
- Эллипс Брокара — эллипс с фокусами в точках Брокара. Его перспектором служит точка Лемуана.
- Эллипс Джонсона. Шесть точек — вершины опорного треугольника и вершины его треугольника Джонсона — лежат на эллипсе Джонсона , имеющем центр в центре девяти точек.
- Эллипс Мандарта треугольника — вписанный в треугольник эллипс, касающийся его сторон в точках касания их с вневписанными окружностями
- Эллипс Штейнера.
- Эннеаграмма (геометрия) — плоская фигура, имеющая девять вершин.
Я[править | править код]
См. также[править | править код]
Примечания[править | править код]
- ↑ Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — С. 130. — 334 с. Архивировано 4 марта 2016 года.
- ↑ Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — 334 с. Архивировано 4 марта 2016 года.. Глава VIII, п. 47, с. 244—245, фиг. 132

























































































































































