Вершинный сепаратор (теория графов)

В теории графов подмножество вершин $S\subset V$ называется вершинным сепаратором для несвязных вершин $a$ и $b$, если удаление $S$ из графа разделяет $a$ и $b$ в две компоненты связности.

Примеры

Сепаратор для решётки.

Предположим, что задана решётка с r строками и c столбцами, тогда полное число n вершин равно r*c. Например, на рисунке, r = 5, c = 8 и n = 40. Если r нечётно, существует одна центральная строка, в противном случае существуют две строки, одинаково близких к центру. Таким же образом, если c нечётно, существует один центральный столбец, в противном случае существуют два столбца, одинаково близких к центру. Выбрав в качестве S одну из этих строк или столбцов, и удалив S из графа, получим разбиение графа на два меньших связных подграфа A и B, каждый из которых содержит максимум n/2 вершин. Если r ≤ c (как на иллюстрации), то выбор центрального столбца даст сепаратор S с r ≤ √n вершинами, и, таким же образом, если c ≤ r, выбор центральной строки даст сепаратор с максимум √n вершинами. Таким образом, любой граф-решётка имеет сепаратор S с размером, не превосходящим √n, удаление которой разделяет граф на две связные компоненты, каждая с размером, не превосходящим n/2.

На левом дереве одна центральная вершина. На правом дереве две центральные вершины. Числа, показанные на рисунке у вершин, показывают эксцентриситет

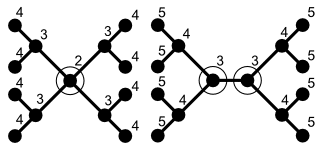
В качестве другого класса примеров можно использовать свободное дерево T, которое имеет сепаратор S, состоящий из одной вершины, удаление которой разделяет T на две (или более) связные компоненты, каждая из которых имеет размер, не превосходящий n/2. Точнее, существует в точности одна или две вершины, в зависимости от того, является ли дерево центрированным или бицентрированным.

Вопреки приведённым примерам не все вершинные сепараторы сбалансированы, но это свойство наиболее полезно для приложений в информатике.

Минимальные сепараторы

Пусть S — (a,b)-сепаратор, то есть подмножество вершин, разделяющее две несвязные вершины a и b. Тогда S является минимальным (a,b)-сепаратором, если никакое подмножество S не разделяет a и b. Множество S называется минимальным сепаратором, если она является минимальным сепаратором для какой-либо пары (a,b) несвязных вершин. Ниже приведено хорошо известный результат, касающийся характеризации минимальных сепараторов:

Лемма. Вершинный сепаратор S в G минимален тогда и только тогда, когда граф $G-S$, полученный удалением S из G, имеет две связные компоненты $C_{1}$ и $C_{2}$, такие что каждая вершина в S связна с некоторой вершиной в $C_{1}$ и некоторой вершиной в $C_{2}$.

Минимальные сепараторы образуют алгебраическую систему: Для двух фиксированных вершин a и b заданного графа G (a,b)-сепаратор S можно рассматривать как предшественник другого (a,b)-сепаратора T, если любой путь из a в b попадает в S прежде чем попасть в T. Более строго, отношение предшествования определяется следующим образом: Пусть S и T — два (a,b)-сепаратора в 'G'. Тогда S является предшественником T, что обозначается как $S\sqsubseteq _{a,b}^{G}T$, если для любой вершины $x\in S\setminus T$ любой путь, соединяющий x и b содержит вершину из T. Из определения следует, что отношение предшествования является предпорядком на множестве всех (a,b)-сепараторов. Более того, Эскаланте (Escalante 1972) доказал, что отношение предшествования становится полной решёткой, если ограничиться множеством минимальных (a,b)-сепараторов G.

Смотрите также

• Хордальный граф — граф, в котором любой минимальный сепаратор является кликой.