Гетероскедастичность
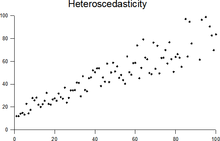
Гетероскедасти́чность (англ. heteroscedasticity) — понятие, используемое в прикладной статистике (чаще всего — в эконометрике), означающее неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели. Гетероскедастичность противоположна гомоскедастичности, означающей однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели.
Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК-оценок параметров. Следовательно, статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей.
Тестирование гетероскедастичности
[править | править код]В первом приближении наличие гетероскедастичности можно заметить на графиках остатков регрессии (или их квадратов) по некоторым переменным, по оцененной зависимой переменной или по номеру наблюдения. На этих графиках разброс точек может меняться в зависимости от значения этих переменных.
Для более строгой проверки применяют, например, статистические тесты Уайта, Голдфелда — Куандта, Бройша — Пагана, Парка, Глейзера, Спирмена.
Оценка модели при гетероскедастичности
[править | править код]Поскольку МНК-оценки параметров моделей остаются несмещёнными состоятельными даже при гетероскедастичности, то при достаточном количестве наблюдений возможно применение обычного МНК. Однако, для более точных и правильных статистических выводов необходимо использовать стандартные ошибки в форме Уайта.
Способы снижения гетероскедастичности
[править | править код]- Использование взвешенного метода наименьших квадратов (ВМНК, WLS). В этом методе каждое наблюдение взвешивается обратно пропорционально предполагаемому стандартному отклонению случайной ошибки в этом наблюдении. Такой подход позволяет сделать случайные ошибки модели гомоскедастичными. В частности, если предполагается, что стандартное отклонение ошибок пропорционально некоторой переменной , то данные делятся на эту переменную, включая константу.
- Замена исходных данных их производными, например, логарифмом, относительным изменением или другой нелинейной функцией. Этот подход часто используется в случае увеличения дисперсии ошибки с ростом значения независимой переменной и приводит к стабилизации дисперсии в более широком диапазоне входных данных.
- Определение «областей компетенции» моделей, внутри которых дисперсия ошибки сравнительно стабильна, и использование комбинации моделей. Таким образом, каждая модель работает только в области своей компетенции, и дисперсия ошибки не превышает заданное граничное значение. Этот подход распространен в области распознавания образов, где часто используются сложные нелинейные модели и эвристики.
Пример
[править | править код]Пусть рассматривается, например, зависимость прибыли от размера активов:
- .
Однако, скорее всего не только прибыль зависит от активов, но и «колеблемость» прибыли не одинакова для той или иной величины активов. То есть скорее всего стандартное отклонение случайной ошибки модели следует полагать пропорциональным стоимости активов:
- .
В этом случае разумнее рассматривать не исходную модель, а следующую:
- ,
предполагая что в этой модели случайные ошибки гомоскедастичны. Можно использовать эту преобразованную модель непосредственно, а можно использовать полученные оценки параметров как оценки параметров исходной модели (взвешенный МНК). Теоретически полученные таким образом оценки должны быть лучше.
См. также
[править | править код]- Тест Голдфелда — Куандта
- Тест Бройша — Пагана
- Тест Парка
- Тест Глейзера
- Тест ранговой корреляции Спирмена
Литература
[править | править код]- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. — М.: Дело, 2004. — 576 с.
- William H. Greene. Econometric analysis. — New York: Pearson Education, Inc., 2003. — 1026 с.



