Закон обратных квадратов
В статье не хватает ссылок на источники (см. рекомендации по поиску). |
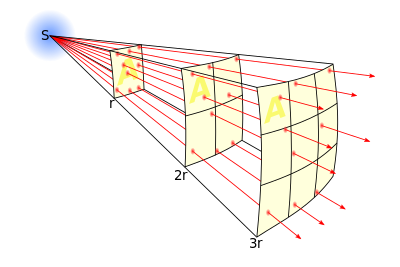
В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.
Обоснование[править | править код]
Закон обратных квадратов в общем случае применим, когда линии действия некоторой силы, энергии или другой величины, расходясь (распространяясь) в радиальном направлении от источника, не теряют своё «полное» значение (то есть величина, под действием которой эти линии расходятся, умноженная на площадь сферы, на радиус которой они расходятся, — сохраняется). По мере того, как площадь сферы (которая определяется по формуле ) растёт пропорционально квадрату расстояния от источника (радиуса сферы), а испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника. Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.
Проявления[править | править код]
Гравитация[править | править код]
Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:
- силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс и обратно пропорциональны квадрату расстояния между ними. Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Если распределение масс в некотором материальном объекте, не являющемся точечным, обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).
Однако, если мы хотим рассчитать силу взаимодействия между произвольными массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данные массивные тела, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то, рассчитывая силу гравитационного взаимодействия между ними, их уже можно целесообразно рассматривать как материальные точки.
Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу [1]. В лекции в 1670 году Гук объяснил, что гравитация свойственна «всем небесным телам» и ввёл принцип, утверждающий, что сила гравитации убывает с расстоянием. К 1679 году Гук пришёл к выводу, что гравитация имеет обратно пропорциональную зависимость квадрату расстояния. Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для Солнечной системы[2], а также отдал дань уважения Буллиальду.
Электростатика[править | править код]
Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними. Это утверждение известно под названием закона Кулона.
Свет и другие виды электромагнитного излучения[править | править код]
Интенсивность света (то есть энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника, обратно пропорциональна квадрату расстояния от источника. Это значит, что, допустим, объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.
Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — 2,6-кратное увеличение расстояния влечёт 6,76-кратное уменьшение интенсивности солнечных лучей.
Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально первой степени расстояния:
Закон обратных квадратов может быть применён только в случае точечных и сферических источников света (например, фонарях): весьма распространённые в помещениях цилиндрические лампы дневного света, тем более помещённые в ряд, не являются точечными источниками (пока их характерный размер не является пренебрежимо малым), и поэтому к ним нельзя применять закон обратных квадратов (пока их характерный размер велик, к ним применим закон обратного расстояния), а равномерно светящаяся плоская поверхность даёт постоянную освещённость на расстояниях, малых по сравнению с её размером.
Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.
Акустические колебания[править | править код]
Энергия сферической звуковой волны так же подчиняется закону обратных квадратов.
Приложения в теории поля[править | править код]
Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.
См. также[править | править код]
Примечания[править | править код]
- ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.
- ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.

