Схема разделения секрета Шамира
Схема интерполяционных полиномов Лагранжа (схема разделения секрета Шамира или схема Шамира) — схема разделения секрета, широко используемая в криптографии. Схема Шамира позволяет реализовать — пороговое разделение секретного сообщения (секрета) между сторонами так, чтобы только любые и более сторон ( ≤ ) могли восстановить секрет. При этом любые и менее сторон не смогут восстановить секрет.
История[править | править код]
В 1979 году израильский криптоаналитик Ади Шамир предложил пороговую схему разделения секрета между сторонами, которая позволяет проводить разделение таким образом, что[1]:
- Для восстановления секрета достаточно и больше сторон.
- Никакие и меньше сторон не смогут получить никакой информации о секрете.
Идея[править | править код]
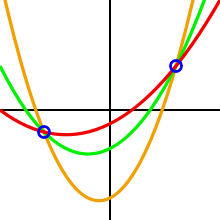
Для интерполяции многочлена степени требуется точек. К примеру, для задания прямой достаточно двух точек, для задания параболы — трех точек, и так далее.
Основная идея данной схемы состоит в том, что интерполяция невозможна, если известно меньшее число точек[1].
Если мы хотим разделить секрет между людьми таким образом, чтобы восстановить его могли только человек ( ≤ ), мы «прячем» его в формулу многочлена степени . Восстановить этот многочлен и исходный секрет можно только по точкам. Количество же различных точек многочлена не ограничено (на практике оно ограничивается размером числового поля, в котором ведутся расчёты)[2].
Описание[править | править код]
Подготовительная фаза[править | править код]
Пусть нужно разделить секрет между сторонами таким образом, чтобы любые участников могли бы восстановить секрет (то есть нужно реализовать -пороговую схему).
Выберем некоторое простое число . Это число можно открыто сообщать всем участникам. Оно задаёт конечное поле размера . Над этим полем построим многочлен степени (то есть случайно выберем все коэффициенты многочлена, кроме )[3]:
В этом многочлене — это разделяемый секрет, а остальные коэффициенты — некоторые случайные числа, которые нужно будет «забыть» после того, как процедура разделения секрета будет завершена[3].
Генерация долей секрета[править | править код]
Теперь вычисляем «доли» — значения построенного выше многочлена, в различных точках, причём ≠ [3]:

Аргументы многочлена (номера секретов) не обязательно должны идти по порядку, главное — чтобы все они были различны по модулю .
После этого каждой стороне, участвующей в разделении секрета, выдаётся доля секрета вместе с номером . Помимо этого, всем сторонам сообщается степень многочлена и размер поля . Случайные коэффициенты и сам секрет «забываются»[3].
Восстановление секрета[править | править код]
Теперь любые участников, зная координаты различных точек многочлена, смогут восстановить многочлен и все его коэффициенты, включая последний из них — разделяемый секрет[3].
Особенностью схемы является то, что вероятность раскрытия секрета в случае произвольных долей оценивается как . То есть в результате интерполяции по точке секретом может быть любой элемент поля с равной вероятностью[2]. При этом попытка полного перебора всех возможных теней не позволит злоумышленникам получить дополнительную информацию о секрете.
Прямолинейное восстановление коэффициентов многочлена через решение системы уравнений можно заменить на вычисление интерполяционного многочлена Лагранжа (отсюда одно из названий метода). Формула многочлена будет выглядеть следующим образом[3]:
где — координаты точек многочлена. Все операции выполняются также в конечном поле [3].
Свойства[править | править код]
К достоинствам данной схемы разделения секрета относят[1]:
- Идеальность: отсутствует избыточность — размер каждой из долей секрета равен размеру секрета.
- Масштабируемость: в условиях схемы число владельцев долей секрета может дополнительно увеличиться вплоть до , где — размер поля, в котором ведутся вычисления. При этом количество долей , необходимых для получения секрета, останется неизменным.
- Динамичность: можно периодически менять используемый многочлен и пересчитывать тени, сохраняя секрет (свободный член) неизменным. При этом вероятность нарушения защиты путем утечки теней уменьшится, так как для получения секрета нужно теней, полученных на одной версии многочлена.
- Гибкость: в тех случаях, когда стороны не являются равными между собой, схема позволяет это учесть путём выдачи сразу нескольких теней одной стороне. Например, пусковой код баллистической ракеты может быть разделён по схеме так, чтобы ракету могли запустить лишь три генерала, которые соберутся вместе, либо любой из генералов и президент, которому при разделении секрета было выдано сразу две тени.
Недостатки[4]:
- Ненадёжность дилера: по умолчанию в схеме предполагается, что тот, кто генерирует и раздаёт тени, надёжен, что не всегда верно.
- Нет проверки корректности теней сторон: участвующая в разделении сторона не может с уверенностью сказать, что её тень подлинна — при подстановке в исходный многочлен получается верное равенство.
Использование[править | править код]
Данная схема нашла применение в аппаратных криптографических модулях, где она используется для многопользовательской авторизации в инфраструктуре открытых ключей[5].
Также схема используется в цифровой стеганографии для скрытой передачи информации в цифровых изображениях[6][7][8][9], для противодействия атакам по сторонним каналам при реализации алгоритма AES[10].
Помимо этого, с помощью схемы Шамира может осуществляться нанесение цифрового водяного знака при передаче цифрового видео[11] и генерация персонального криптографического ключа, используемого в биометрических системах аутентификации[12].
Пример[править | править код]
Пусть нужно разделить секрет «11» между 5 сторонами. При этом любые 3 стороны должны иметь возможность восстановить этот секрет. То есть нужно реализовать -пороговую схему[3].
Возьмём простое число . Построим многочлен степени :
В этом многочлене — это разделяемый секрет, а остальные коэффициенты 7 и 8 — некоторые случайные числа, которые нужно будет «забыть» после того, как процедура разделения секрета будет завершена.
Теперь вычисляем координаты 5 различных точек:
После этого ключи (вместе с их номером, числом и степенью многочлена ) раздаются сторонам. Случайные коэффициенты и сам секрет «забываются».
Теперь любые 3 участника смогут восстановить многочлен и все его коэффициенты, включая последний из них — разделённый секрет. Например, чтобы восстановить многочлен по трём долям им нужно будет решить систему:
Очевидно, что с меньшим числом известных секретов получится меньше уравнений и систему решить будет нельзя (даже полным перебором решений).
Построим интерполяционный многочлен Лагранжа:
Получим исходный многочлен:
Последний коэффициент многочлена — — и является секретом[3].
См. также[править | править код]
Примечания[править | править код]
- ↑ 1 2 3 Shamir A. How to share a secret (англ.) // Communications of the ACM — New York City: Association for Computing Machinery, 1979. — Vol. 22, Iss. 11. — P. 612—613. — ISSN 0001-0782 — doi:10.1145/359168.359176
- ↑ 1 2 Чмора А.Л. Современная прикладная криптография. — 2-е изд., стер.. — М.: Гелиос АРВ, 2002. — С. 123—124. — 256 с. — ISBN 5-85438-046-3.
- ↑ 1 2 3 4 5 6 7 8 9 Шнайер Б. 23.2 Алгоритмы разделения секрета. Схема интерполяционных полиномов Лагранжа // Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — С. 588—589. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.
- ↑ Dawson E., Donovan D. The breadth of Shamir's secret-sharing scheme (англ.) // Computers & Security — Elsevier BV, 1994. — Vol. 13, Iss. 1, 69-78. — ISSN 0167-4048; 1872-6208 — doi:10.1016/0167-4048(94)90097-3
- ↑ P. Luo, A. Yu-Lun Lin, Z. Wang, M. Karpovsky. Hardware Implementation of Secure Shamir's Secret Sharing Scheme (англ.) // HASE '14 Proceedings of the 2014 IEEE 15th International Symposium on High-Assurance Systems Engineering : Proceeding. — Washington, DC, USA: IEEE Computer Society, 2014. — P. 193—200. — ISSN 978-1-4799-3466-9. — doi:10.1109/HASE.2014.34.
- ↑ Chia-Chun Wu , Shang-Juh Kao, Wen-Chung Kuo, Min-Shiang Hwang. Reversible Secret Image Sharing Based on Shamir's Scheme (англ.) // IIH-MSP '09 Proceedings of the 2009 Fifth International Conference on Intelligent Information Hiding and Multimedia Signal Processing : Proceeding. — Washington, DC, USA: IEEE Computer Society, 2009. — P. 1014—1017. — ISBN 978-0-7695-3762-7. — doi:10.1109/IIH-MSP.2009.158.
- ↑ Ulutas M., Ulutaş G., Nabiyev V. V. Medical image security and EPR hiding using Shamir's secret sharing scheme (англ.) // Journal of Systems and Software — Elsevier BV, 2011. — Vol. 84, Iss. 3. — P. 341–353. — ISSN 0164-1212; 1873-1228 — doi:10.1016/J.JSS.2010.11.928
- ↑ S. Salim, S. Suresh, R. Gokul, Reshma S. Application of Shamir Secret Sharing Scheme for Secret Data Hiding and Authentication (англ.) // International Journal of Advanced Research in Computer Science & Technology : Journal. — 2014. — Vol. 2, no. 2. — P. 220—224. — ISSN 2347-8446.
- ↑ Che-Wei Lee, Wen-Hsiang Tsai. A data hiding method based on information sharing via PNG images for applications of color image authentication and metadata embedding (англ.) // Signal Processing : Journal. — Amsterdam, The Netherlands: Elsevier North-Holland, Inc., 2013. — Vol. 93, no. 7. — P. 2010—2025. — ISSN 0165-1684. — doi:10.1016/j.sigpro.2013.01.009.
- ↑ Goubin L., Martinelli A. Protecting AES with Shamir’s Secret Sharing Scheme (англ.) // Cryptographic Hardware and Embedded Systems — CHES 2011: 13th International Workshop, Nara, Japan, September 28 — October 1, 2011, Proceedings / B. Preneel, T. Takagi — Berlin, Heidelberg, New York City, London: Springer Science+Business Media, 2011. — P. 79—94. — 524 p. — (Lecture Notes in Computer Science; Vol. 6917) — ISBN 978-3-642-23950-2 — ISSN 0302-9743; 1611-3349 — doi:10.1007/978-3-642-23951-9_6
- ↑ Xiao S., Ling H., Zou F., Lu Z. Secret Sharing Based Video Watermark Algorithm for Multiuser (англ.) // Digital Watermarking: 7th International Workshop, IWDW 2008, Busan, Korea, November 10-12, 2008, Selected Papers / H. J. Kim, S. Katzenbeisser, A. T. S. Ho — Berlin, Heidelberg, New York City, London: Springer Berlin Heidelberg, 2009. — P. 303—312. — 472 p. — (Lecture Notes in Computer Science; Vol. 5450) — ISBN 978-3-642-04437-3 — ISSN 0302-9743; 1611-3349 — doi:10.1007/978-3-642-04438-0_26
- ↑ A. Teoh, D. Ngo, A. Goh. Personalised cryptographic key generation based on FaceHashing (англ.) // Computers and Security : Journal. — Elsevier Advanced Technology Publications Oxford, 2004. — Vol. 23, no. 7. — P. 606—614. — ISSN 0167-4048. — doi:10.1016/j.cose.2004.06.002.
Литература[править | править код]
- Shamir A. How to share a secret (англ.) // Communications of the ACM — New York City: Association for Computing Machinery, 1979. — Vol. 22, Iss. 11. — P. 612—613. — ISSN 0001-0782 — doi:10.1145/359168.359176
- Шнайер Б. 23.2 Алгоритмы разделения секрета. Схема интерполяционных полиномов Лагранжа // Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — С. 588—589. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.
- Чмора А.Л. Современная прикладная криптография. — 2-е изд., стер.. — М.: Гелиос АРВ, 2002. — С. 123—124. — 256 с. — ISBN 5-85438-046-3.
- Под общ. ред. Ященко В.В. Введение в криптографию. — 2-е изд., испр.. — М.: МЦНМО: «ЧеРо», 1999. — С. 118—125. — 272 с. — ISBN 5-900916-40-5.
Ссылки[править | править код]
ssss: реализация схемы разделения секретов Шамира с интерактивной демонстрацией.
Эта статья входит в число добротных статей русскоязычного раздела Википедии. |
































