SOSEMANUK
Sosemanuk — синхронный поточный шифр, разработанный в ноябре 2004 года группой французских учёных во главе с Комом Бербеном (фр. Côme Berbain)[1]. В апреле 2008 года стал одним из финалистов проекта eStream по профилю 1 (высокоэффективные поточные шифры для программной реализации)[2]. Согласно портфолио проекта eStream, Sosemanuk представляет собой полностью свободное программное обеспечение с открытым исходным кодом, которое может быть использовано для любых целей, включая коммерческие[3].
Аннотация[править | править код]
В основе Sosemanuk лежит поточный шифр SNOW 2.0 и усечённый вариант блочного шифра SERPENT. Его длина ключа варьируется между 128 и 256 битами, а для инициализации используется 128-битное начальное значение (англ. initial value). Как утверждают авторы шифра, любая длина ключа обеспечивает 128-битную безопасность.[4]
Шифр устойчив ко всем известным видам атак. Самая успешная атака на Sosemanuk оценивалась 2138 порядком сложности, что, тем не менее, хуже заявленной сложности в 128 бит[5].
В реализации шифра Sosemanuk были исправлены некоторые структурные недостатки SNOW 2.0, а также увеличена производительность за счёт уменьшения размера внешних и статических данных.
Общая схема работы[править | править код]

Как и поточный шифр SNOW, алгоритм Sosemanuk использует два основных понятия: регистр сдвига с линейной обратной связью (LFSR) и конечный автомат (FSM). Так, данные, полученные с помощью LFSR, поступают на вход FSM, где происходит их нелинейное преобразование. Затем к четырём выходным значениям конечного автомата применяется табличная замена (S-box) и XOR с соответствующими значениями регистра сдвига. Расписание ключей для шифра составляется с помощью примитива Serpent24 — усечённого варианта SERPENT. Кроме того, выходные значения двенадцатого, восемнадцатого и двадцать четвёртого раунда Serpent24 используются для инъекции начального значения: задания состояния LSM и регистров FSM.[4]
Следует заметить, что Sosemanuk использует регистр сдвига длины 10, тогда как в SNOW его длина равнялась шестнадцати. Кроме того, в FSM операция применения S-box заменена на операцию Trans, представляющую собой умножение над 32-битным полем и последующий побитовый циклический сдвиг.[6]
Спецификация[4][править | править код]
Sosemanuk использует два основных понятия шифра SNOW: регистр сдвига с линейной обратной связью (LFSR) и конечный автомат (FSM). Кроме того, используются два примитива из алгоритма SERPENT: serpent1 и serpent24.
Serpent1 — один раунд SERPENT, без смешивания с ключом и линейного преобразования. Представляет собой использование таблицы подстановок (S-box), при этом входные 128 бит, разбитые на четыре 32-битных слова, преобразуются в выходные четыре 32-битных слова.
Serpent24 — алгоритм SERPENT, использующий 24 раунда из 32. Последний раунд является полным, при этом включает в себя линейное преобразование и XOR с 25-м раундовым ключом. В Sosemanuk используется для инициализации в режиме шифрования.
Регистр сдвига с линейной обратной связью[править | править код]

Sosemanuk использует линейный регистр сдвига длины 10 над конечным 32-битным полем .
В начальный момент времени происходит инициализация регистра сдвига 32-битными значениями . Затем, на каждом шаге вычисляется новое значение по формуле:
.
Обратная связь регистра сдвига задается многочленом:
Здесь — корень примитивного многочлена над полем :
— корень примитивного многочлена над полем :
Поле представляет собой отношение , а конечное поле получается из отношения . Последовательность является периодической с максимальным периодом .

Конечный автомат[править | править код]
Sosemanuk использует конечный автомат с 64 битами памяти, что соответствует двум 32-битным регистрам и . Он принимает на вход несколько значений, полученных с помощью LFSR, обновляет регистры, после чего выдаёт 32-битное значение по схеме:
— последний значащий бит (используется little-endian нотация).
(шестнадцатеричная запись первых десяти знаков числа π)
— побитовый циклический сдвиг.
Выходное преобразование[править | править код]
К четырём выходным значениям конечного автомата применяется алгоритм Serpent1, после чего к результату и соответствующим значениям, полученным из регистра сдвига, применяется операция XOR:
Схема шифрования[править | править код]
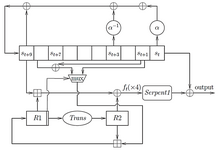
Для получения выходных значений используется связка LFSR и FSM. В начальный момент времени LFSR инициализируется значениями , а в регистры FSM записываются значения и . В момент времени выполняются следующие действия:
- Обновление FSM: вычисляются значения , и , исходя из известных , , , и .
- Обновление LFSR: вычисляется , значение переходит во внутренний буфер, регистр сдвига сдвигается.
Каждые четыре шага из промежуточных значений , , , и значений внутреннего буфера , , , посредством применения Serpent1 и XOR вычисляются итоговые значения Авторы шифра рекомендуют шифровать группы по четыре байта, используя при этом прямой (little-endian) порядок байтов для увеличения производительности.
Расписание ключей и введение начального значения[править | править код]
В шифре Sosemanuk процесс инициализации происходит в два этапа:
- Задается расписание ключей (key schedule), в котором секретный ключ не зависит от начального значения
- Вводится начальное значение (IV injection), при этом используется заданное расписание ключей и IV. Таким образом, происходит инициализация внутреннего состояния поточного шифра.
Key shedule[править | править код]
Расписание ключей шифра Sosemanuk задается с помощью Serpent24, который предоставляет 25 128-битных раундовых ключей. Эти ключи идентичны первым 25 ключам, полученным из расписания ключей SERPENT. Несмотря на то, что можно задать ключ любой длины от 128 до 256, шифр обеспечивает лишь 128-битную безопасность, вследствие чего длина ключа 128 считается стандартной.
IV injection[править | править код]
Для введения IV используются выходные значения двенадцатого, восемнадцатого и двадцать четвёртого раунда Serpent24.
— выходные значения 12-го раунда
— выходные значения 18-го раунда
— выходные значения 24-го раунда
Начальные значения LFSR и FSM:
Известные атаки[править | править код]
Атаки, предусмотренные разработчиками[4][править | править код]
Компромисс времени и данных[править | править код]
Атака компромисса времени и данных (англ. Time-memory-data tradeoff attack) основана на предположении, что злоумышленнику известен алгоритм шифрования и выходное значение. Авторы шифра рассматривают случай восстановления пары «ключ — начальное значение». В связи с 128-битной длиной ключа и такой же длиной начального значения сложность такой атаки оценивается 2128 количеством операций.
«Предполагай и определяй»[править | править код]
Атака «Предполагай и определяй» (англ. Guess and determine attack) основана на утверждении, что, предполагая значения нескольких ключей, злоумышленник может восстановить все внутреннее состояние. Авторы шифра рассматривают данный вид атаки в предположении, что злоумышленник получает значения шести 32-битных ключей. В этом случае сложность атаки составляет 256 бит.
Корреляционная атака[править | править код]
По утверждению авторов, известные корреляционные атаки (англ. Correlation attacks) на шифр SNOW не имеет смысла применять к шифру Sosemanuk, в связи с тем, что линейные соотношения входных и выходных данных не сохраняются после применения алгоритма Serpent1.
Различающая атака[править | править код]
В описании шифра рассмотрены известные на момент разработки различающие атаки (англ. Distinguishing attacks) на шифр SNOW. В явном виде они не могут быть применены к Sosemanuk из-за сложности подбора маски после применения Serpent1.
Алгебраическая атака[править | править код]
Разработчики шифра считают, что ни одна из известных на момент разработки алгебраических атак (англ. Algebraic attacks) не применима к шифру ввиду невозможности явно вычислить алгебраическую иммунность (англ. algebraic immunity) выходных функций от входных значений.
Новые атаки[править | править код]
После того, как шифр стал широко известен в криптографическом сообществе, в литературе было опубликовано несколько новых атак на Sosemanuk. Тем не менее, изначально заявленная сложность в 128 бит так и не была взломана.http://www.ecrypt.eu.org/stream/e2-sosemanuk.html[5]
Guess-and-Determine Attack, 2006[7][править | править код]
В 2006 году коллектив учёных из Японии и Ирана, Юкиясу Цуно (Yukiyasu Tsunoo) Теруо Сайто (Teruo Saito) и др., представили атаку «Предполагай и определяй» сложностью 2224. Для её осуществления необходимо знать 16 слов ключевого потока. При этом, увеличение длины ключа ведет к уменьшению сложности атаки.
Атака основывается на предположении, что последний значащий бит в регистре конечного автомата в момент времени равен нулю. Если при это утверждение не выполняется, взломать шифр данным способом не получится.
Для осуществления атаки необходимо предположить значения
Using Linear Masks Attack, 2008[8][править | править код]
В 2008 году на конференции ASIACRYPT[англ.] учёные из Кореи Юнг-Кеун Ли, Донг Хун Ли и Парк Сангву представили корреляционную атаку на Sosemanuk с помощью использования метода линейной маски (linear masking method). Сложность такой атаки составляла 2148, и внутреннее 384-битное состояние восстанавливалось с вероятностью 99 %. Для проведения атаки используется линейная аппроксимация с коэффициентом корреляции 2−21.41, построенная по словам ключевого потока и начальному состоянию регистра сдвига. При этом, начальное состояние LFSR восстанавливается с помощью быстрого преобразования Уолша.
Примечания[править | править код]
- ↑ Sosemanuk Algorithm forencryption and decryption Video on Demand (VoD) (PDF Download Available) (англ.). ResearchGate. Дата обращения: 14 октября 2017. Архивировано 15 октября 2017 года.
- ↑ The eSTREAM portfolio page (англ.). www.ecrypt.eu.org. Дата обращения: 14 октября 2017. Архивировано 13 февраля 2017 года.
- ↑ The eSTREAM Project - eSTREAM Phase 3. www.ecrypt.eu.org. Дата обращения: 14 октября 2017. Архивировано 4 сентября 2012 года.
- ↑ 1 2 3 4 Архивированная копия. Дата обращения: 7 декабря 2010. Архивировано 27 мая 2011 года.
- ↑ 1 2 The eSTREAM portfolio page (англ.). www.ecrypt.eu.org. Дата обращения: 16 декабря 2017. Архивировано 5 апреля 2016 года.
- ↑ Patrik Ekdahl and Thomas Johansson. A New Version of the Stream Cipher SNOW (англ.) // Springer-Verlag Berlin Heidelberg 2003. Архивировано 14 декабря 2017 года.
- ↑ [http://www.ecrypt.eu.org/stream/papersdir/2006/009.pdf Evaluation of SOSEMANUK With Regard to Guess-and-Determine Attacks] (англ.) // eSTREAM portfolio. Архивировано 13 января 2017 года.
- ↑ [https://link.springer.com/content/pdf/10.1007%2F978-3-540-89255-7.pdf Cryptanalysis of Sosemanuk and SNOW 2.0 Using Linear Masks] (англ.) // J. Pieprzyk (Ed.): ASIACRYPT 2008, LNCS 5350, pp. 524–538, 2008..
Литература[править | править код]
- «Sosemanuk, a fast software-oriented stream cipher», описание разработчиков
- «Evaluation of SOSEMANUK With Regard to Guess-and-Determine Attacks»
- «Cryptanalysis of Sosemanuk and SNOW 2.0 Using Linear Masks»
Для улучшения этой статьи желательно:
|
![{\displaystyle F_{2^{32}}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dbfb230807947e31e9a9bfd665f79f89b241680)



![{\displaystyle \pi (X)=\alpha X^{10}+\alpha \pi ^{-1}X^{7}+X+1\subseteq F_{2^{32}}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4300e807c26d6f2c193afc84ea0f6c4fce097ae0)

![{\displaystyle F_{2^{8}}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa1da4ec41f42afe4d9710fe7adf2806e9555e86)


![{\displaystyle F_{2}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e07111aad63220551b5b4ab0db9836dc27e7d9c)

![{\displaystyle F_{2}[X]/Q(X)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8accde44caba266a1467e841f53e1b6b70fe972)
![{\displaystyle F_{2^{8}}[X]/P(X)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/249bae350aaaf7bc4df67dd7b85e29bdcc413862)









































