Регистр сдвига с линейной обратной связью
Регистр сдвига с линейной обратной связью (РСЛОС, англ. linear feedback shift register, LFSR) — сдвиговый регистр битовых слов, у которого значение входного (вдвигаемого) бита равно линейной булевой функции от значений остальных битов регистра до сдвига. Может быть организован как программными, так и аппаратными средствами. Применяется для генерации псевдослучайных последовательностей битов, что находит применение, в частности, в криптографии[1]. По похожему принципу работают регистр сдвига с обратной связью по переносу и регистр сдвига с обобщённой обратной связью.
Описание[править | править код]

В регистре сдвига с линейной обратной связью (РСЛОС) выделяют две части (модуля):
- собственно регистр сдвига;
- схему (или подпрограмму) обратной связи, вычисляющую значение вдвигаемого бита.
Регистр состоит из функциональных ячеек памяти (битов одного или нескольких машинных слов), в каждой из которых хранится текущее состояние (значение) одного бита. Количество ячеек , называют длиной регистра. Биты (ячейки) обычно нумеруются числами , содержимое -й ячейки обозначается через . Значение нового бита определяется до сдвига битов в регистре и только после сдвига записывается в ячейку , а из ячейки извлекается очередной сгенерированный бит.
Функцией обратной связи для РСЛОС является линейная булева функция от значений всех или некоторых битов регистра. Функция выполняет умножение битов регистра на коэффициенты , где . Количество коэффициентов совпадает с количеством битов регистра . Коэффициенты принимают значения , причём последний коэффициент равен , так как РСЛОС задаётся характеристическим многочленом степени . Сложение по модулю 2 (операция «XOR», обозначаемая в формулах символом «») или её логическая инверсия «XNOR» являются линейными булевыми функциями и наиболее часто применяются в таких регистрах[2]. При этом биты, являющиеся переменными функции обратной связи, называются отводами, а сам регистр называется конфигурацией Фибоначчи[3].
Управление регистром в аппаратных реализациях производится подачей сдвигающего импульса (иначе называемого тактовым или синхроимпульсом) на все ячейки. Управление регистром в программных реализациях производится выполнением цикла. На каждой итерации цикла вычисляется функция обратной связи и выполняется битовый сдвиг в слове.
Принцип работы[править | править код]
В течение каждого такта сдвигового регистра с линейной обратной связью выполняет следующие операции:
- читается бит, расположенный в ячейке ; этот бит является очередным битом выходной последовательности;
- функции обратной связи вычисляет новое значение для ячейки , используя текущие значения ячеек;
- содержимое каждой -й ячейки перемещается в следующую ячейку , где ;
- в ячейку записывается бит, ранее вычисленный функцией обратной связи.
Если функция обратной связи выполняет логическую операцию «XOR» (исключающее ИЛИ), значения бит (ячеек) могут быть вычислены по следующим формулам[4]:
Свойства[править | править код]
Периодичность[править | править код]
Периодом регистра сдвига называется минимальная длина получаемой последовательности до начала её повторения. РСЛОС длины имеет начальных состояний, задающих значения бит в ячейках. Из них состояний - ненулевые, так что генерируемая последовательность имеет период . Период генерируемой последовательности максимален и равен , если многочлен обратной связи (или характеристический многочлен) над полем является примитивным. Для этого необходимо (но не достаточно) выполнение следующих 2-х условий:
- чётное число отводов;
- номера отводов, взятые все вместе, а не попарно, взаимно просты.
Число всех возможных примитивных многочленов равно , где - функция Эйлера[5]. Регистр, заданный таким многочленом, называется регистром сдвига максимального периода (или генератором псевдослучайной последовательности), а генерируемые последовательности - последовательностями максимального периода (или М-последовательностями)[4][6].
Линейная сложность[править | править код]
Линейной сложностью бесконечной двоичной последовательности называется число , которое определяется следующим образом:
- если — нулевая последовательность, то ;
- если не существует РСЛОС, который генерирует , то ;
- в противном случае равна длине самого короткого РСЛОС, который генерирует .
Линейной сложностью конечной двоичной последовательности называется число , равное длине самого короткого РСЛОС, который генерирует эту последовательность.
Линейная сложность регистра сдвига с линейной обратной связью показывает, насколько близка генерируемая последовательность к случайной. Эффективным алгоритмом определения линейной сложности конечной бинарной последовательности является алгоритм Берлекэмпа-Мэсси.
Корреляционная независимость[править | править код]
Пытаясь получить высокую линейную сложность генерируемой последовательности, криптографы нелинейно объединяют выходы нескольких регистров сдвига. При этом одна или несколько выходных последовательностей (или даже выходы отдельных РСЛОС) могут быть связаны общим потоком и вскрыты криптоаналитиком. Взлом на основе такой уязвимости называют корреляционным вскрытием. Основная идея такого взлома заключается в обнаружении некоторой корреляции между выводом генератора и выводами его составных частей. Затем, наблюдая выходную последовательность, можно получить информацию об этих промежуточных выводах, и, таким образом, взломать генератор. Томас Сигенталер показал, что можно точно определить корреляционную независимость, и что существует компромисс между корреляционной независимостью и линейной сложностью[7].
Программная реализация[править | править код]
Программные реализации РСЛОС достаточно медленны и работают быстрее, если они написаны на ассемблере. Одно из решений - параллельное использование 16-ти РСЛОС (или 32-х, в зависимости от длины слова в архитектуре компьютера). В такой схеме используется массив слов, размер которого равен длине регистра сдвига, а каждый бит слова относится к своему РСЛОС. Так как используются одинаковые номера отводных последовательностей, то это может дать заметный выигрыш в производительности генератора[3].
Конфигурация Фибоначчи[править | править код]
Рассмотрим 32-битовый сдвиговый регистр. Для него имеется отводная последовательность . Это означает, что для генерации нового бита необходимо с помощью операции XOR просуммировать 31-й, 30-й, 29-й, 27-й, 25-й и 0-й биты. Полученный РСЛОС имеет максимальный период . Код для такого регистра на языке Си следующий:
int LFSR_Fibonacci (void)
{
static unsigned long S = 0x00000001;
S = ((((S >> 31) ^ (S >> 30) ^ (S >> 29) ^ (S >> 27) ^ (S >> 25) ^ S ) & 0x00000001 ) << 31 ) | (S >> 1);
return S & 0x00000001;
}
Конфигурация Галуа[править | править код]
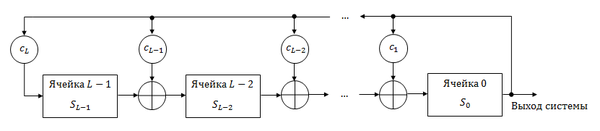
Как и в конфигурации Фибоначчи, схема обратной связи представляет собой набор операций XOR отводных битов с выходом генератора, но порядок битов в регистре обратный: входным является -й бит, а выходным — -й. Результат сложения записывается в следующую ячейку, а новый выходной бит записывается в -ю. Таким образом, если генерируемый бит равен нулю, то все биты в ячейках сдвигаются вправо без изменений, если генерируемый бит равен единице, то биты отвода меняют своё значение на противоположное, и все биты сдвигаются вправо. И конфигурация Фибоначчи, и конфигурация Галуа одной и той же длины генерируют одинаковые, но смещённые по времени одна от другой последовательности (при этом внутренние состояния регистров могут отличаться)[8].
Данный генератор не обладает большей криптостойкостью, но он даёт выигрыш в производительности: все операции XOR посредством распараллеливания можно выполнить за одно действие, а не последовательно одна за другой, как в конфигурации Фибоначчи. Данная схема также даст выигрыш при аппаратной реализации.
Код для регистра сдвига длины 32 бит на языке Си следующий:
int LFSR_Galois (void)
{
// for polynomial 0x80000057, reversed 0xea000001
static unsigned long S = 0x00000001;
if (S & 0x00000001) {
S = ((S ^ 0x80000057) >> 1) | 0x80000000;
return 1;}
else {
S >>= 1;
return 0;}
}
Стоит отметить, что цикл из фиксированного числа вызовов функции LFSR_Galois в конфигурации Галуа выполняется примерно в 2 раза быстрее, чем функция LFSR_Fibonacci в конфигурации Фибоначчи (компилятор MS VS 2010 на Intel Core i5).
Пример генерируемой последовательности[править | править код]
Конфигурация Фибоначчи[править | править код]

Пусть РСЛОС задаётся характеристическим многочленом . Это значит, что битами отвода будут 2-й и 0-й, а единица в формуле многочлена означает, что 0-й бит - входной. Функция обратной связи имеет вид . Допустим, изначальным состоянием регистра сдвига была последовательность . Дальнейшие состояния регистра приведены в таблице ниже:
| Номер шага | Состояние | Генерируемый бит |
|---|---|---|
| 0 | 1 | |
| 1 | 0 | |
| 2 | 0 | |
| 3 | 1 | |
| 4 | 1 | |
| 5 | 1 | |
| 6 | 0 | |
| 7 | 1 |
Поскольку внутреннее состояние на седьмом шаге вернулось к исходному, то, начиная со следующего шага, будет идти повтор битов. То есть генерируемая последовательность такова: (порядок бит в последовательности соответствует порядку их генерации РСЛОС). Таким образом, период последовательности равен 7, то есть максимально возможному значению, что произошло в силу примитивности заданного многочлена.
Конфигурация Галуа[править | править код]

Возьмём тот же характеристический многочлен, то есть , . С выходным битом складывается только 1-й бит. Начальное состояние то же самое. Дальнейшие состояния регистра:
| Номер шага | Состояние | Генерируемый бит |
|---|---|---|
| 0 | 1 | |
| 1 | 1 | |
| 2 | 1 | |
| 3 | 0 | |
| 4 | 1 | |
| 5 | 0 | |
| 6 | 0 | |
| 7 | 1 |
Внутреннее состояние регистра на седьмом шаге вернулось к исходному, следовательно, его период также равен 7.
Пример реализации на логических элементах[править | править код]

На картинке справа можно увидеть пример реализации РСЛОС с конфигурацией Галуа вида (7, 10).
В верхней части схемы расположены выходные контакты, на которых можно увидеть последовательность генерируемых регистром битов. Ниже идут D-триггеры, которые соединены друг с другом и образуют собственно регистр. Самый правый триггер (номер 1) является выходным и, согласно реализуемой конфигурации, влияет на передачу бита из 10-го и 7-го триггеров (берётся XOR передаваемого и выходного бита). Остальные биты передаются без изменений.
Начальная конфигурация регистра задаётся при помощи мультиплексоров перед каждым триггером. Чтобы сбросить конфигурацию регистра до начальной (или той, которая нужна, её можно выбрать на контактах перед мультиплексорами), нужно всего лишь подать 1 на контакт Init, после чего подать сигнал синхронизации. После зануления синхронизации регистр примет нужную конфигурацию. Чтобы дальше он начал работать корректно, сигнал Init нужно вновь занулить.
Матричное представление LFSR[править | править код]
Этот раздел статьи ещё не написан. |
Генерация примитивных многочленов[править | править код]
Вычисление примитивного многочлена над полем — достаточно сложная математическая задача: для генерации примитивного многочлена степени нужно знать множители числа . Проще случайным образом выбрать многочлен и проверить его на примитивность[3]. Ещё один метод заключается в использовании готовых таблиц, в которых приведены номера отводных последовательностей, обеспечивающих максимальный период генератора. Ниже приведена таблица примитивных многочленов над полем для регистров сдвига максимального периода длиной до 19 бит[5]. Стоит учесть, что у генератора любой заданной длины может быть более одного примитивного многочлена согласно их свойствам. Полный список для регистров длиной от 4 до 32 бит можно найти здесь.
| Биты, | Примитивный многочлен | Период, | Число примитивных многочленов |
|---|---|---|---|
| 2 | 3 | 1 | |
| 3 | 7 | 2 | |
| 4 | 15 | 2 | |
| 5 | 31 | 6 | |
| 6 | 63 | 6 | |
| 7 | 127 | 18 | |
| 8 | 255 | 16 | |
| 9 | 511 | 48 | |
| 10 | 1023 | 60 | |
| 11 | 2047 | 176 | |
| 12 | 4095 | 144 | |
| 13 | 8191 | 630 | |
| 14 | 16383 | 756 | |
| 15 | 32767 | 1800 | |
| 16 | 65535 | 2048 | |
| 17 | 131071 | 7710 | |
| 18 | 262143 | 7776 | |
| 19 | 524287 | 27594 | |
| 20 - 168 | [1] | ||
| 2 - 786, 1024, 2048, 4096 | [2] | ||
Преимущества и недостатки[править | править код]
Преимущества[править | править код]
- высокое быстродействие криптографических алгоритмов, создаваемых на основе РСЛОС (например потоковых шифров);
- применение только простейших битовых операций сложения и умножения, аппаратно реализованных практически во всех вычислительных устройствах;
- хорошие криптографические свойства (РСЛОС могут генерировать последовательности большого периода с хорошими статистическими свойствами);
- благодаря своей структуре, РСЛОС легко анализируются с использованием алгебраических методов.
Недостатки[править | править код]
- Одна из главных проблем РСЛОС в том, что их программная реализация крайне неэффективна: приходится избегать разреженных многочленов обратной связи, так как они приводят к облегчению взлома корреляционным вскрытием, а плотные многочлены очень медленно просчитываются. Поэтому программная реализация такого генератора работает не быстрее, чем реализация DES.
- Линейность последовательности на выходе регистра позволяет однозначно определить многочлен обратной связи по последовательным битам с помощью алгоритма Берлекэмпа — Мэсси или алгоритма Евклида[3][4].
- Относительная лёгкость анализа алгебраическими методами не только облегчает разработку, но и увеличивает шансы на взлом генератора на базе РСЛОС.
Способы улучшения криптостойкости генерируемых последовательностей[править | править код]
Генераторы с несколькими регистрами сдвига[править | править код]

Генератор такого типа состоит из нескольких регистров сдвига с линейной обратной связью, которые генерируют биты соответственно. Далее, генерируемые биты преобразуются некоторой булевой функцией . Необходимо отметить, что у генераторов такого типа длины регистров , , взаимно просты между собой.
Период данного генератора равен , где — общее число ячеек. Следовательно, использование нескольких РСЛОС увеличивает период генерируемой последовательности по сравнению с одним регистром, что увеличивает криптостойкость генератора. Также увеличивается линейная сложность или длина кратчайшего регистра, соответствующего данному генератору. Такой регистр находится с помощью алгоритма Берлекэмпа — Мэсси по генерируемой последовательности. В лучшем случае его длина соизмерима с периодом генерируемой последовательности[4].
Генераторы с нелинейными преобразованиями[править | править код]
Структурная схема такого генератора ничем не отличается от схемы предыдущего генератора. Главное отличие заключается в том, что устройство преобразования задано нелинейной булевой функцией . В качестве такой функции берётся, например, полином Жегалкина (согласно теореме Жегалкина, всякая булева функция единственным образом может быть представлена полиномом Жегалкина).
Нелинейный генератор может быть также реализован на регистре сдвига с нелинейной обратной связью. Он может дать вариантов последовательностей максимального периода, что больше, чем у РСЛОС[5].
Криптостойкость данного генератора повышается за счет нелинейности используемой функции. Определение состояния регистров по генерируемой последовательности битов является сложной математической задачей, потому что не известен алгоритм, восстанавливающий исходные состояния.
Данный метод используется, например, в генераторе Геффа и обобщённом генераторе Геффа, однако такие генераторы могут быть взломаны корреляционным вскрытием[7].
Генераторы с различным тактированием регистров сдвига[править | править код]


Генератор «стоп-пошёл»[править | править код]
Генератор «стоп-пошёл» (англ. Stop-and-Go, Both-Piper) использует вывод РСЛОС-1 для управления тактовой частотой РСЛОС-2, так что РСЛОС-2 меняет своё состояние в некоторый момент времени , только если выход РСЛОС-1 в момент времени был равен единице. Данная схема не устояла перед корреляционным вскрытием[3].
В целях увеличения криптостойкости был предложен чередующийся генератор «стоп-пошёл». В нём используются три регистра сдвига различной длины. Здесь РСЛОС-1 управляет тактовой частотой 2-го и 3-го регистров, то есть РСЛОС-2 меняет своё состояние, когда выход РСЛОС-1 равен единице, а РСЛОС-3 - когда выход РСЛОС-1 равен нулю. Выходом генератора является операция сложения по модулю два выходов РСЛОС-2 и РСЛОС-3. У данного генератора большой период и большая линейная сложность. Существует способ корреляционного вскрытия РСЛОС-1, но это не сильно ослабляет криптографические свойства генератора.
Усложнённая схема тактирования использована в двустороннем генераторе «стоп-пошёл», в котором используются 2 регистра сдвига одинаковой длины. Если выход РСЛОС-1 в некоторый момент времени равен нулю, а в момент времени - единице, то РСЛОС-2 не тактируется в момент времени . Если выход РСЛОС-2 в момент времени равен нулю, а в момент времени - единице, и если этот регистр тактируется в момент времени , то в этот же момент РСЛОС-1 не тактируется. Линейная сложность данной схемы примерно равна периоду генерируемой последовательности.
Самопрореживающий генератор[править | править код]
Самопрореживающие (англ. self-decimated) генераторы управляют собственной частотой. Существует два типа таких генераторов. Первый был предложен Рэйнером Рюппелом. Он состоит из регистра сдвига и схемы с линейной обратной связью, которая тактирует этот регистр в зависимости от того, какими получаются выходные значения регистра сдвига. Если выход РСЛОС равен единице, то регистр тактируется с одной частотой, а если выход равен нулю - то с другой. Второй тип был предложен Биллом Чамберсом и Дитером Коллманом. В схему обратной связи поступает не сам выходной сигнал, а результат операции XOR определённых битов РСЛОС.
Существуют также прореживаемый (англ. shrinking) и самопрореживаемый (англ. self-shrinking) генераторы. Они достаточно новые, и не все их свойства хорошо изучены. Первый использует два РСЛОС. Если на генератор подать тактовый импульс, и выходом РСЛОС-1 является единица, то выходом генератора будет выход РСЛОС-2. В противном случае, при подаче тактового импульса оба бита сбрасываются, тактирование начинается заново. Во втором генераторе вместо проверки выходов двух регистров на 0 или 1 проверяются 2 бита одного регистра.
Прореживаемый генератор может быть взломан, если многочлены обратной связи прорежены. Кроме того, его скорость генерации не постоянна. Для самопрореживаемого генератора нужно примерно в 2 раза меньше памяти, чем первому, но при этом он работает в 2 раза медленнее[7].
Многоскоростной генератор с внутренним произведением[править | править код]
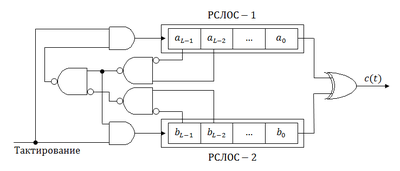
Данный генератор использует два регистра сдвига РСЛОС-1 и РСЛОС-2. Тактовая частота РСЛОС-2 в раз больше, чем у РСЛОС-1. Определённые биты этих регистров перемножаются друг с другом операцией AND. Результаты умножений суммируются операцией XOR, и получается выходная последовательность. Этот генератор имеет высокую линейную сложность и обладает хорошими статистическими свойствами. Однако его состояние может быть определено по выходной последовательности длиной , где и — длины РСЛОС-1 и РСЛОС-2 соответственно, а — отношение их тактовых частот.
Каскад Голлманна[править | править код]

Данная схема представляет собой улучшенную версию генератора «стоп-пошёл». Он состоит из последовательности РСЛОС, тактирование каждого из которых управляется предыдущим РСЛОС. Если выходом РСЛОС-1 в момент времени является 1,то тактируется РСЛОС-2. Если выходом РСЛОС-2 в момент времени является 1, то тактируется РСЛОС-3, и так далее. Выход последнего РСЛОС является выходом генератора. Если длина всех РСЛОС одинакова и равна , то период системы из РСЛОС равен , а линейная сложность - [7].
Эта идея проста и может быть использована для генерации последовательностей с огромными периодами, большими линейными сложностями и хорошими статистическими свойствами. Но, к сожалению, они чувствительны к вскрытию, называемому запиранием (англ. lock-in), когда криптоаналитик, восстанавливая сначала входную последовательность последнего регистра в каскаде, взламывает весь каскад, регистр за регистром. С ростом числа регистров генерируемая последовательность приближается к случайной, так что лучше использовать больше РСЛОС небольшой длины, чем меньше длинных РСЛОС.
Мажоритарные генераторы[править | править код]

Мажоритарный (или пороговый) генератор состоит из большого числа регистров сдвига, выводы которых поступают на устройство, заданное функцией мажорирования, например, мажоритарный элемент. Особенность данного генератора заключается в том, что каждый из регистров сдвига имеет свой тактовый бит , , которые и являются переменными мажоритарной функции. Например, для трёх регистров такая функция имеет вид . Сдвигаются только те регистры, чьи тактовые биты равны значению , то есть сдвиг регистров происходит по большинству значений таких битов: 0 или 1.
Таким образом, мы получаем генератор с переменным числом РСЛОС. Его линейная сложность , где — длина -го регистра[7]. Недостатками такого генератора являются возможность прямого перебора и корреляционного вскрытия (каждый выходной бит дает некоторую информацию о состоянии сдвигового регистра, а точнее - 0.189 бита).
Подобные генераторы используются в алгоритмах шифрования A5 (A5/1, A5/2).
Применение[править | править код]
Регистры сдвига с линейной обратной связью могут быть реализованы аппаратными средствами, что позволяет их использовать для быстрой генерации псевдослучайной последовательности, например при расширении спектра методом прямой последовательности или для генерации шумового сигнала[9].
Использование в криптографии[править | править код]
Регистры сдвига с линейной обратной связью издавна применяются в качестве генераторов псевдослучайной последовательности для потоковых шифров (особенно в военной криптографии). Однако РСЛОС представляет собой линейную схему и в некоторых случаях может быть легко взломан. Например, криптоаналитик может перехватить часть зашифрованного текста и по нему с помощью вышеупомянутого алгоритма Берлекэмпа — Мэсси восстановить РСЛОС минимального размера, который имитирует оригинальный РСЛОС. Затем, перехваченный текст может быть подан на полученный регистр и расшифрован. Методы увеличения криптостойкости потоковых шифров, основанных на РСЛОС, приведены выше.
На регистре сдвига с линейно обратной связью основаны такие потоковые шифры, как A5/1 и A5/2, используемые в стандарте GSM, и шифр E0, используемый в Bluetooth. Шифр A5/2 был взломан, а шифры A5/1 и E0 имеют серьёзные недостатки[10][11].
Регистр сдвига с линейной обратной связью тесно связан с линейным конгруэнтным генератором[12].
Использование в качестве счётчиков[править | править код]
Периодичность генерируемой последовательности РСЛОС позволяет использовать его в качестве делителя тактовой частоты или счётчика[13]. Счётчик на основе такого генератора имеет упрощенную схему обратной связи, в отличие от обычных двоичных счётчиков или счётчиков кода Грея, и, следовательно, может работать на высоких тактовых частотах. Однако необходимо убедиться, чтобы такой счётчик никогда не входил в нулевое состояние.
Тестирование цифровых устройств[править | править код]
В отличие от обычного счётчика, РСЛОС переходит из одного состояния в другое не в порядке двоичного счёта, что позволяет его использовать для генерации тестового сигнала при обнаружении ошибок в логических схемах[6].
Также регистры сдвига с линейной обратной связью применяются во встроенных системах самоконтроля (англ. built-in self-test, BIST) для сигнатурного анализа (выявления ошибочных битов) в логических схемах. Подобные системы применяют ввиду ограниченности числа выводов микросхем (не все промежуточные значения битов можно подать на выход). Система BIST представляет собой 3 блока: генератор тестовой последовательности и сигнатурный анализатор, которые и строятся на основе РСЛОС, и контроллер тестов. Регистр сдвига в анализаторе «сжимает» результат схемы на тестовую последовательность в сигнатуру и продолжает работать до тех пор, пока всего его биты, кроме 0-го, не станут равными нулю, то есть до состояния . Наряду с РСЛОС работает двоичный счётчик, подсчитывающий количество тактов с момента окончания сжатия тестовой реакции. Если изначальное состояние регистра соответствовало эталонной сигнатуре (сигнатуре безошибочной схемы), то показание счётчика соответствует номеру ошибочного бита[14][15].
Так как РСЛОС производит сжатие с потерей данных, то есть вероятность, что в схеме с ошибками получившаяся сигнатура будет равна эталонной. Этого можно избежать, используя сигнатурный анализатор с несколькими входами.
Скремблирование[править | править код]
Регистры сдвига с линейной обратной связью применяются при скремблировании с целью получения цифрового потока со свойствами случайной последовательности. Псевдослучайная последовательность РСЛОС максимальной длины складывается по модулю 2 с потоком передаваемых битов, причём генерация последовательности происходит с той же скоростью, что и передача данных. Некоторые системы и технологии, использующие скремблирование:
- ATSC[16];
- DAB;
- DVB-T;
- NICAM;
- CDMA;
- 100BASE-T2 Fast Ethernet;
- 1000BASE-T Gigabit Ethernet;
- PCI Express 3.0;
- SATA;
- Serial Attached SCSI;
- USB 3.0;
- IEEE 802.11a;
- Bluetooth LE.
См. также[править | править код]
Примечания[править | править код]
- ↑ Б. Скляр, 2007.
- ↑ Linear Feedback Shift Registers in Virtex Devices. Дата обращения: 19 ноября 2014. Архивировано 2 ноября 2013 года.
- ↑ 1 2 3 4 5 Б. Шнайер, 2013.
- ↑ 1 2 3 4 Габидулин, Кшевецкий, Колыбельников, 2011.
- ↑ 1 2 3 Ю.Б. Кобзарев, 2013.
- ↑ 1 2 Ларин, 2008.
- ↑ 1 2 3 4 5 Фомичёв, 2003.
- ↑ Beker, Piper, 1982.
- ↑ А. Сизоненко, 2012.
- ↑ E. Barklan, E. Biham, N. Keller, 2008.
- ↑ Y. Lu, W. Meier, S. Vaudenay, 2005.
- ↑ D. Eastlake, J. Schiller, S. Crocker, 2005.
- ↑ Efficient Shift Registers, LFSR Counters and Long Pseudo-Random Sequence Generators. Дата обращения: 18 ноября 2014. Архивировано 25 января 2021 года.
- ↑ B. Harrington, 2008.
- ↑ О. Дяченко.
- ↑ В. Варгаузин, 1999.
Литература[править | править код]
- Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. — Триумф, 2013. — 816 с. — ISBN 978-5-89392-527-2.
- Габидулин Э. М., Кшевецкий А. С., Колыбельников А. И. Защита информации: учебное пособие — М.: МФТИ, 2011. — 225 с. — ISBN 978-5-7417-0377-9
- Ларин А. Л. Основы цифровой электроники — М.: МФТИ, 2008. — 314 с. — ISBN 978-5-7417-0228-4
- Скляр Б. Цифровая связь. Теоретические основы и практическое применение. — Вильямс, 2007. — 1104 с. — ISBN 978-5-8459-0497-3.
- Кобзарев Ю. Б. Современная радиолокация. — Рипол Классик, 2013. — 708 с. — ISBN 978-5-4584-7357-6.
- Фомичёв В. М. Дискретная математика и криптология: Курс лекций / под ред. Н. Д. Подуфалов — М.: Диалог-МИФИ, 2013. — 397 с. — ISBN 978-5-86404-185-7
- Beker H., Piper F. Cipher systems: the protection of communications (англ.) — London: Northwood Books, 1982. — 427 p. — ISBN 978-0-7198-2611-5
- Сизоненко А. Б. Многоканальный цифровой источник шума на основе рекуррентного регистра сдвига. — Журнал «Спецтехника и связь» №3, 2012. Архивная копия от 29 ноября 2014 на Wayback Machine
- Barklan E., Biham E., Keller N. Instant ciphertext-only cryptanalysis of GSM encrypted communication. — Journal of cryptology №21-3, 2008.
- Lu Y., Meier W., Vaudenay S. Instant ciphertext-only Cryptanalysis of GSM encrypted communication. — Crypto №3621, 2005. (недоступная ссылка)
- Eastlake D., Schiller J., Crocker S. Randomness requirements for security. — 2005.
- Harrington B. Get your boost from BIST. — 2008. (недоступная ссылка)
- Дяченко О. Н. Компактный анализ над полем GF(3).
- Варгаузин В. Принципы цифрового телевидения стандарта ATSC. — Журнал Теле-Спутник №9(47), 1999.
Ссылки[править | править код]
- LFSR reference (англ.). Теория и реализация LFSR, последовательности максимальной длины и полные таблицы отводных последовательностей для длин от 7 до 16 миллионов (от 3 до 24 битов), а также частичные таблицы для длин до 4 миллиардов (от 25 до 32 битов) (недоступная ссылка) Архивировано 1 октября 2018.
- International telecommunications union recommendation O.151 (англ.). Август 1992
- Pseudo-random number generation routine Архивная копия от 25 декабря 2008 на Wayback Machine (англ.)
- [3] (англ.)
- Simple explanation of LFSRs for engineers (англ.)
- Feedback terms (англ.)
- An implementation of a cryptographically secure shrinking pseudorandom number generator (англ.)
- Методы и задачи криптографической защиты информации (недоступная ссылка)






































![{\displaystyle \left[0,\;0,\;1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8af933a7da57168d447bce9a8e6ec159f7cc731b)
![{\displaystyle \left[1,\;0,\;0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adeea0aeded816fbd21e3e8d353496d24d466c30)
![{\displaystyle \left[1,\;1,\;0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0b72d18d0c77d29b7bc06cceb73712f8e8eb5b5)
![{\displaystyle \left[1,\;1,\;1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/226d164a13cbd78997e6b81962e2288d179c84db)
![{\displaystyle \left[0,\;1,\;1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45a94dcb0e53aff06e1257befe98a51fcf4d19ed)
![{\displaystyle \left[1,\;0,\;1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34adbd6217aa4312249d4d194d31ed56484fb71e)
![{\displaystyle \left[0,\;1,\;0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ce9f5119c5c08c8c24c983b58856226898d84d)
![{\displaystyle \left[1,\;0,\;0,\;1,\;1,\;1,\;0,\;1\;...\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc39fe3548ce53cd5902dfcf19ce290059f2e28d)
















































![{\displaystyle \left[1,\;0,\;0,\;...,\;0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd0adfa3a098cafc9bb92f3162db89b070a58985)