Арбелос

Сапожный нож.

Арбелос.

Арбелос (греч. άρβυλος — сапожный нож) — плоская геометрическая фигура. На прямой взяты три точки A, B и C. Построены три полуокружности с диаметрами AB, BC и AC, расположенные по одну сторону от этой прямой. Фигура, ограниченная этими полуокружностями, и называется арбелос.

Свойства

Теорема Паппа Александрийского

Теорема Паппа: $h_1=d_1$, $h_2=2d_2$,…, $h_n=nd_n$.

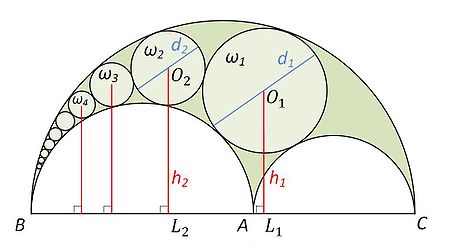
Даны арбелос ABC (точка A лежит между точками B и C) и окружности $\omega_1$, $\omega_2$,…,$\omega_n$ ($n\in N$), причем окружность $\omega_1$ касается дуг AB, BC и AC, а при $n\ge 2$ окружность $\omega_n$ касается дуг AB и BC и окружности $\omega_{n-1}$. Тогда при любом натуральном $n$ расстояние от центра окружности $\omega_n$ до прямой BC равно произведению диаметра этой окружности на ее номер $n$:

$h_n=nd_n$.

Площадь

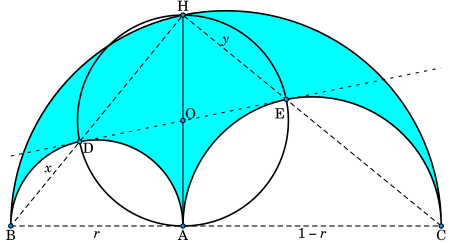
Площадь арбелоса равна площади круга с диаметром HA.

$S=\frac{1}{4}\pi HA^2$

Прямоугольник

Отрезок BH пересекает полуокружность BA в точке D. Отрезок CH пересекает полуокружность AC в точке E. Тогда DHEA является прямоугольником.

Касательные

Прямая DE касается полуокружности BA в точке D и полуокружности AC в точке E.

Литература

• Mortimer Brian. The Geometry of The Arbelos. — Carleton University, 1998.