Точка округления
Точка округления (круговая точка, омбилическая точка или омбилика) ― точка на гладкой регулярной поверхности в евклидовом пространстве, в которой нормальные кривизны по всем направлениям равны.
Название «омбилика» происходит от французского «ombilic», которое, в свою очередь, происходит от латинского «umbilicus» ― «пуп».
Свойства[править | править код]
В точке округления:
- главные кривизны поверхности совпадают.
- Первая квадратичная форма и вторая квадратичная форма поверхности пропорциональны.
- любое касательное направление является главным направлением.
- Соприкасающийся параболоид является параболоидом вращения.
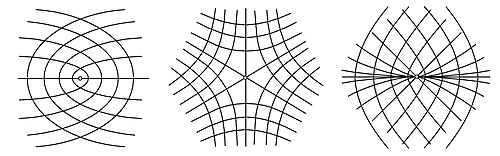
- Индикатриса Дюпена является окружностью.
- Сеть линий кривизны (то есть линий, касающихся в каждой точке одного из главных направлений поверхности), имеет особенность[1].
- Любая точка округления является либо эллиптической точкой поверхности (если главные кривизны не равны нулю, и следовательно, гауссова кривизна поверхности в данной точке положительная), либо так называемой плоской точкой округления (если главные кривизны равны нулю, и следовательно, гауссова кривизна и средняя кривизна поверхности в данной точке равны нулю). В первом случае в малой окрестности точки округления поверхность похожа на сферу, а во втором — на плоскость.
Примеры[править | править код]

В евклидовом пространстве с метрикой :
- Сфера целиком состоит из эллиптических точек округления.
- Трёхосный эллипсоид (с попарно различными осями) имеет ровно четыре точки округления, все они эллиптические и относятся к типу «лимон».
- Плоскость целиком состоит из плоских точек округления.
- Обезьянье седло имеет изолированную плоскую точку округления в начале координат.
Гипотеза Каратеодори[править | править код]
Каратеодори высказал гипотезу, что на любой достаточно гладкой замкнутой выпуклой поверхности M в трёхмерном евклидовом пространстве существуют как минимум две точки округления. Эта гипотеза была впоследствии доказана при дополнительном предположении, что поверхность M аналитическая[2][3].
Обобщение[править | править код]
Пусть ― гладкое многообразие произвольной размерности в евклидовом пространстве большей размерности. Тогда в каждой точке определены собственных значений пары первой и второй квадратичных форм, заданных на касательном расслоении . Точка называется омбиликой, если в ней набор содержит хотя бы два совпадающих числа. Множество омбилик имеет коразмерность 2, то есть задается на двумя независимыми уравнениями.[4] Так, омбилические точки на поверхности общего положения изолированы (), а на трёхмерном многообразии общего положения они образуют кривую ().
Литература[править | править код]
- Топоногов В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 9785891552135.
- Рашевский П. К. Курс дифференциальной геометрии, — Любое издание.
- Фиников С. П. Курс дифференциальной геометрии, — Любое издание.
- Фиников С. П. Теория поверхностей, — Любое издание.
- Porteous I.R. Geometric Differentiation for the intelligence of curves and surfaces — Cambridge University Press, Cambridge, 1994.
- Struik D. J. Lectures on Classical Differential Geometry, — Addison Wesley Publ. Co., 1950. Reprinted by Dover Publ., Inc., 1988.
Примечания[править | править код]
- ↑ 1 2 Ремизов А. О. Многомерная конструкция Пуанкаре и особенности поднятых полей для неявных дифференциальных уравнений, ― СМФН, 19 (2006), 131—170.
- ↑ Zbl 1056.53003. Дата обращения: 13 октября 2014. Архивировано 19 октября 2014 года.
- ↑ Иванов В. В. Аналитическая гипотеза Каратеодори, ― Сиб. матем. журн., 43:2 (2002), 314—405. Дата обращения: 13 октября 2014. Архивировано 10 ноября 2014 года.
- ↑ Арнольд В. И. Математические методы классической механики, ― Любое издание. (Добавление 10. Кратности собственных частот и эллипсоиды, зависящие от параметров).








