Лестница Мёбиуса: различия между версиями

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
Следующая правка →
Содержимое удалено Содержимое добавлено
ВизуальныйВики-текст
Переведена статья "Möbius ladder"
(нет различий)

Версия от 16:07, 7 декабря 2014

Два представления лестницы Мёбиуса M16. Для анимации трансформации из одного вида в другой смотрите файл [1].
Представление лестницы Мёбиуса M16 в виде ленты Мёбиуса.

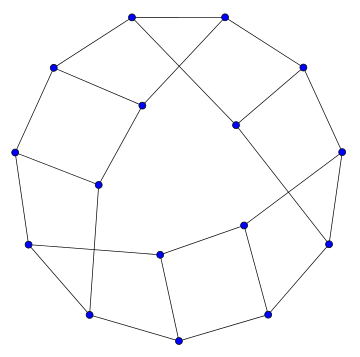
В теории графов лестница Мёбиуса Mn — это кубический циркулянтный граф с чётным числом n вершин, образованный из цикла с n вершинами путём добавления рёбер (называемых "перекладинами"), соединяющих противоположные пары вершин цикла. Он назван так ввиду того, что (за исключением M6 = K3,3) Mn имеет в точности n/2 циклов длины 4[1], соединённых вместе общими рёбрами и образующих топологически ленту Мёбиуса. Лестницы Мёбиуса изучали Гай и Харари (Guy & Harary 1967).

Свойства

Любая лестница Мёбиуса является непланарным вершинным[англ.] графом. Число скрещиваний[англ.]* лестницы Мёбиуса равно единице, и граф может быть вложен без самопересечений в тор или проективную плоскость. Таким образом, они являются примерами тороидальных графов. Ли (Li 2005) изучал вложение этих графов в поверхности более высоких родов.

Лестницы Мёбиуса являются вершинно-транзитивными, но (снова, за исключением M6) не рёберно-транзитивными — каждое ребро цикла, из которого лестница образована, принадлежит единственному 4-рёберному циклу, в то время как каждая перекладина принадлежит двум таким циклам.

Если n ≡ 2 (mod 4), Mn является двудольным. Если n ≡ 0 (mod 4), по теореме Брукса хроматическое число Mn равно 3. Де Мьер и Ной (De Mier & Noy 2004) показали, что лестница Мёбиуса однозначно определяется её многочленом Тутте[англ.].

Лестница Мёбиуса M8 имеет 392 остовных дерева. Этот граф и M6 имеют наибольшее число остовных деревьев среди кубических графов с тем же числом вершин.[2] Однако среди кубических графов с 10 вершинами наибольшее число остовных деревьев у графа Петерсена, который не является лестницей Мёбиуса.

Многочлены Тутте[англ.] лестниц Мёбиуса можно получить по простой рекуррентной формуле.[3]

Миноры графа

Граф Вагнера M8

Лестницы Мёбиуса играют важную роль в теории миноров графа?!. Самым ранним результатом такого типа является теорема Вагнера (Wagner 1937), о том, что граф, не содержащий K5 миноров, может быть образован с использованием сумм по клике?! для комбинирования планарных графов и лестницы Мёбиуса M8. По этой причине M8 называют графом Вагнера?!.

Губсер (Gubser 1996) определяет почти-планарный граф как непланарный граф, у которого любой нетривиальный минор планарен. Он показал, что 3-связные почти-планарные графы являются лестницами Мёбиуса или принадлежат небольшому числу других семейств, и что остальные почти-планарные графы можно получить из этих графов с помощью ряда простых операций.

Махарри (Maharry 2000) показал, что почти все графы, не содержащие куб в качестве минора, могут быть получены из лестниц Мёбиуса в результате последовательного применения простых операций.

Химия и физика

Валба, Ричардс и Халтивангер (Walba, Richards & Haltiwanger 1982) первыми синтезировали молекулярную структуру, имеющую форму лестницы Мёбиуса, и с тех пор эта структура представляет интерес для химиков и химической стереографии [4], особенно в свете похожих на лестницу молекул ДНК. Имея это ввиду, Флапан (Flapan 1989) изучала математические симметрии вложений лестниц Мёбиуса в R3.

Лестницы Мёбиуса используются как модель сверхпроводимого кольца в экспериментах по изучению эффектов топологии проводимости при взаимодействии электронов.[5]

Комбинаторная оптимизация

Лестницы Мёбиуса используются также в информатике как часть подхода целочисленного программирования к задачам упаковки множеств и линейного упорядочивания. Некоторые конфигурации в этих задачах могут быть использованы для определения граней политопов, описывающих ослабление условий[англ.] линейного программирования. Эти грани называются ограничениями лестниц Мёбиуса.[6]

Смотрите также

Примечания

  1. ↑ McSorley, 1998.
  2. ↑ Jakobson, Rivin, 1999; Valdes, 1991.
  3. ↑ Biggs, Damerell, Sands, 1972.
  4. ↑ Simon, 1992.
  5. ↑ Mila, Stafford, Capponi, 1998; Deng, Xu, Liu, 2002.
  6. ↑ Bolotashvili, Kovalev, Girlich, 1999; Borndörfer, Weismantel, 2000; Grötschel, Jünger, Reinelt, 1985; Newman, Vempala, 2001

Ссылки

  • N. L. Biggs, R. M. Damerell, D. A. Sands. Recursive families of graphs // Journal of Combinatorial Theory. — 1972. — Т. 12. — С. 123–131. — doi:10.1016/0095-8956(72)90016-0.
  • G. Bolotashvili, M. Kovalev, E. Girlich. New facets of the linear ordering polytope // SIAM Journal on Discrete Mathematics. — 1999. — Т. 12, вып. 3. — С. 326–336. — doi:10.1137/S0895480196300145.
  • Ralf Borndörfer, Robert Weismantel. Set packing relaxations of some integer programs // Mathematical Programming. — 2000. — Т. 88, вып. 3. — С. 425–450. — doi:10.1007/PL00011381.
  • Wen-Ji Deng, Ji-Huan Xu, Ping Liu. Period halving of persistent currents in mesoscopic Möbius ladders // Chinese Physics Letters. — 2002. — Т. 19, вып. 7. — С. 988–991. — doi:10.1088/0256-307X/19/7/333. — arXiv:cond-mat/0209421.
  • Erica Flapan. Symmetries of Möbius ladders // Mathematische Annalen. — 1989. — Т. 283, вып. 2. — С. 271–283. — doi:10.1007/BF01446435.
  • M. Grötschel, M. Jünger, G. Reinelt. On the acyclic subgraph polytope // Mathematical Programming. — 1985. — Т. 33. — С. 28–42. — doi:10.1007/BF01582009.
  • M. Grötschel, M. Jünger, G. Reinelt. Facets of the linear ordering polytope // Mathematical Programming. — 1985. — Т. 33. — С. 43–60. — doi:10.1007/BF01582010.
  • Bradley S. Gubser. A characterization of almost-planar graphs // Combinatorics, Probability and Computing. — 1996. — Т. 5, вып. 3. — С. 227–245. — doi:10.1017/S0963548300002005.
  • Richard K. Guy, Frank Harary. On the Möbius ladders // Canadian Mathematical Bulletin. — 1967. — Т. 10. — С. 493–496. — doi:10.4153/CMB-1967-046-4.
  • Dmitry Jakobson, Igor Rivin. On some extremal problems in graph theory. — 1999. — arXiv:math.CO/9907050.
  • De-ming Li. Genus distributions of Möbius ladders // Northeastern Mathematics Journal. — 2005. — Т. 21, вып. 1. — С. 70–80.
  • John Maharry. A characterization of graphs with no cube minor // Journal of Combinatorial Theory. — 2000. — Т. 80, вып. 2. — С. 179–201. — doi:10.1006/jctb.2000.1968.
  • John P. McSorley. Counting structures in the Möbius ladder // Discrete Mathematics. — 1998. — Т. 184, вып. 1–3. — С. 137–164. — doi:10.1016/S0012-365X(97)00086-1.
  • Anna De Mier, Marc Noy. On graphs determined by their Tutte polynomials // Graphs and Combinatorics. — 2004. — Т. 20, вып. 1. — С. 105–119. — doi:10.1007/s00373-003-0534-z.
  • Frédéric Mila, C. A. Stafford, Sylvain Capponi. Persistent currents in a Möbius ladder: A test of interchain coherence of interacting electrons // Physical Review B. — 1998. — Т. 57, вып. 3. — С. 1457–1460. — doi:10.1103/PhysRevB.57.1457.
  • Alantha Newman, Santosh Vempala. Integer Programming and Combinatorial Optimization: 8th International IPCO Conference, Utrecht, The Netherlands, June 13–15, 2001, Proceedings. — Berlin: Springer-Verlag, 2001. — Т. 2081. — С. 333–347. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-45535-3_26.
  • Jonathan Simon. New scientific applications of geometry and topology (Baltimore, MD, 1992). — Providence, RI: American Mathematical Society, 1992. — Т. 45. — С. 97–130. — (Proceedings of Symposia in Applied Mathematics).
  • L. Valdes. Proceedings of the Twenty-second Southeastern Conference on Combinatorics, Graph Theory, and Computing (Baton Rouge, LA, 1991). — 1991. — Т. 85. — С. 143–160. — (Congressus Numerantium).
  • K. Wagner. Über eine Eigenschaft der ebenen Komplexe // Mathematische Annalen. — 1937. — Т. 114. — С. 570–590. — doi:10.1007/BF01594196.
  • D. Walba, R. Richards, R. C. Haltiwanger. Total synthesis of the first molecular Möbius strip // Journal of the American Chemical Society. — 1982. — Т. 104, вып. 11. — С. 3219–3221. — doi:10.1021/ja00375a051.

Внешние ссылки

Источник — https://ru.wikipedia.org/w/index.php?title=Лестница_Мёбиуса&oldid=67209397