Бикасательные плоской кривой четвёртой степени
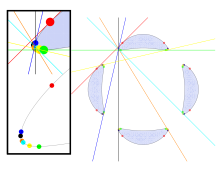
Плоская кривая четвёртой степени общего вида имеет 28 бикасательных, то есть прямых, касающихся кривой в двух точках. Эти прямые существуют в комплексной проективной плоскости, но можно найти кривые, для которых все 28 из этих прямых имеют вещественные числа в качестве координат, а потому принадлежит евклидовой плоскости.
Явные кривые четвёртого порядка с двадцатью восемью вещественными бикасательными первым нашёл Юлиус Плюккер[1][2]. Как показал Плюккер, число вещественных бикасательных любой кривой четвёртого порядка должно быть равно 28, 16 или должно быть меньше 9. Другую кривую четвёртого порядка с 28 вещественными бикасательными можно образовать как геометрическое место точек центров эллипсов с фиксированными длинами осей, касающихся двух непараллельных прямых[3]. Шиода[4] дал другое построение кривых четвёртого порядка с двадцатью восемью бикасательными, которая образуется проекцией кубической поверхности. Двадцать семь бикасательных кривой Шиода вещественны, а двадцать восьмая является бесконечно удалённой прямой в проективной плоскости.
Пример[править | править код]
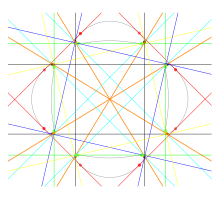
Кривая Тротта, другая кривая с 28 вещественными бикасательными, является множеством точек (x,y), удовлетворяющих уравнению четвёртой степени
Эти точки образуют несингулярную кривую четвёртого порядка, имеющую род три и двадцать восемь вещественных бикасательных[5].
Подобно примеру Плюкера и кривой Блюма и Гуинанда, кривая Тротта имеет четыре раздельных (неправильных) овала, максимальное число для кривых четвёртого порядка, а потому является M-кривой. Четыре овала можно сгруппировать в шесть различных пар овалов. Для каждой пары овалов имеется четыре бикасательных, касающихся обоих овалов в паре, две прямые разделяют овалы и две не разделяют. Кроме того, каждый овал ограничивает невыпуклую область плоскости и имеет одну бикасательную, связывающую невыпуклые порции границы.
Связь с другими структурами[править | править код]
Двойственная кривая (первичной) кривой четвёртого порядка имеет 28 вещественных обыкновенных двойных точек, двойственных 28 бикасательным первичной кривой.
28 бикасательных кривой четвёртого порядка могут быть сопоставлены символам вида
где a, b, c, d, e и f равны нулю или единице и для них выполняется
Существует 64 комплекта a, b, c, d, e и f, но только 28 из них дают нечётную сумму. Можно интерпретировать a, b и c как однородные координаты точки плоскости Фано, а d, e и f как координаты прямой в той же конечной проективной плоскости. Условие нечётности суммы эквивалентно требованию, что точка не лежит на прямой, и существует 28 различных пар таких точек и прямых.
Точки и прямые плоскости Фано, образующие неинцидентные пары, образуют треугольник, и бикасательные кривой четвёртого порядка можно рассматривать как соответствующие 28 треугольникам плоскости Фано[8]. Графом Леви плоскости Фано служит граф Хивуда, в котором треугольники плоскости Фано представлены 6-циклами. 28 6-циклов графа Хивуда, в свою очередь, соответствуют 28 вершинам графа Коксетера[9].
28 бикасательных кривой четвёртого порядка также соответствуют 56 парам прямых поверхности дель Пеццо степени 2[8] и 28 нечётным тэта-характеристикам.
27 прямых кривой третьего порядка и 28 бикасательных кривой четвёртого порядка, вместе со 120 трикасательными плоскостями канонической кривой шестого порядка рода 4 образуют «„троицу“» Арнольда, точнее, образуют соответствие Маккея[10][11][12] и могут быть связаны с многими другими объектами, включая E7 и E8, как обсуждается в статье «ADE-классификация».
Примечания[править | править код]
- ↑ Plücker, 1839.
- ↑ Gray, 1982.
- ↑ Blum, Guinand, 1964.
- ↑ Shioda, 1995.
- ↑ Trott, 1997.
- ↑ Riemann, 1876.
- ↑ Cayley, 1879.
- ↑ 1 2 Manivel, 2006.
- ↑ Dejter, 2011.
- ↑ le Bruyn, 2008.
- ↑ Arnold, 1997, с. 13.
- ↑ McKay, Sebbar, 2007, с. 11.
Литература[править | править код]
- Blum R., Guinand A. P. A quartic with 28 real bitangents // Canadian Mathematical Bulletin. — 1964. — Т. 7. — С. 399–404. — doi:10.4153/cmb-1964-038-6.
- Arthur Cayley. On the bitangents of a quartic // Salmon's Higher Plane Curves. — 1879. — С. 387–389.. В книге The collected mathematical papers of Arthur Cayley, Andrew Russell Forsyth, ed., The University Press, 1896, vol. 11, pp. 221—223.
- Jeremy Gray. From the history of a simple group // The Mathematical Intelligencer. — 1982. — Т. 4, вып. 2. — С. 59–67. — doi:10.1007/BF03023483.
- The Eightfold Way / Silvio Levy. — Cambridge University Press, 1999. — Т. 35. — С. 115–131. — (MSRI Publications). — ISBN 0-521-66066-1.
- Manive L. Configurations of lines and models of Lie algebras // Journal of Algebra. — 2006. — Т. 304, вып. 1. — С. 457–486. — doi:10.1016/j.jalgebra.2006.04.029.
- Julius Plücker. Theorie der algebraischen Curven: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie. — Berlin: Adolph Marcus, 1839.
- Manivel L. Configurations of lines and models of Lie algebras // Journal of Algebra. — 2006. — Т. 304, вып. 1. — С. 457–486. — doi:10.1016/j.jalgebra.2006.04.029.
- Riemann G. F. B. Zur Theorie der Abel'schen Funktionen für den Fall p = 3 // Ges. Werke. — Leipzig, 1876. — С. 456–472.. Как цитировано у Кэли.
- Tetsuji Shioda. Weierstrass transformations and cubic surfaces // Commentarii Mathematici Universitatis Sancti Pauli. — 1995. — Т. 44, вып. 1. — С. 109–128.
- Michael Trott. Applying GroebnerBasis to Three Problems in Geometry // Mathematica in Education and Research. — 1997. — Т. 6, вып. 1. — С. 15–28.
- Italo J. Dejter. From the Coxeter graph to the Klein graph // Journal of Graph Theory. — 2011. — doi:10.1002/jgt.20597. — arXiv:1002.1960.
- Lieven le Bruyn. Arnold’s trinities. — 2008. — Июнь. Архивировано 11 апреля 2011 года.
- Vladimir Arnold. 1997, Toronto Lectures, Lecture 2: Symplectization, Complexification and Mathematical Trinities. — 1997. — С. 13. TeX, PostScript, Онлайн-письма Арнольда
- Italo J. Dejter. From the Coxeter graph to the Klein graph // Journal of Graph Theory. — 2011. — doi:10.1002/jgt.20597. — arXiv:1002.1960.
- McKay J., Sebbar A. Replicable Functions: An introduction // Frontiers in Number Theory, Physics, and Geometry, II. — Springer, 2007. — С. 373–386. — doi:10.1007/978-3-540-30308-4_10.

![{\displaystyle \left[{\begin{array}{ccc}a&b&c\\d&e&f\\\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f9c527454b1e1f26c9be9078ebac08b5492bbfc)
