Гиперграф
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 5 апреля 2021 года; проверки требует 1 правка.
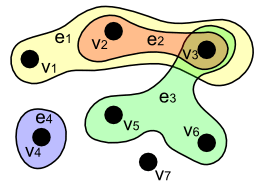
Гипергра́ф — обобщение графа, в котором каждым ребром могут соединяться не только две вершины, но и любые подмножества множества вершин.
С математической точки зрения, гиперграф представляет собой пару , где — непустое множество объектов некоторой природы, называемых вершинами гиперграфа, а — семейство непустых (необязательно различных) подмножеств множества , называемых рёбрами гиперграфа.
Гиперграфы применяются, в частности, при моделировании электрических цепей.
Трансверсалью гиперграфа является множество , содержащее непустое пересечение с каждым ребром. Такая трансверсаль будет минимальной, если никакое её подмножество само не является трансверсалью гиперграфа.
Литература[править | править код]
- В. А. Емеличев, О. И. Мельников, В. И. Сарванов, Р. И. Тышкевич. Глава XI: Гиперграфы // Лекции по теории графов. — М.: Наука, 1990. — С. 298—315. — 384 с. — ISBN 5-02-013992-0.
- И. А. Головинский. Методы анализа топологии коммутационных схем электрических сетей // Электричество. — 2005. — № № 3. — С. 10—18.
- В. А. Евстигнеев, В. Н. Касьянов. Толковый словарь по теории графов. — Новосибирск: Наука, 1999. Архивная копия от 29 июня 2008 на Wayback Machine
- А. А. Зыков. Гиперграфы // Успехи математических наук. — 1974. — № 6 (180).







