Дерево (структура данных)
Дерево — одна из наиболее широко распространённых структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Является связным графом, не содержащим циклы. Большинство источников также добавляет условие на то, что рёбра графа не должны быть ориентированными. В дополнение к этим трём ограничениям, в некоторых источниках указывается, что рёбра графа не должны быть взвешенными.
Определения[править | править код]
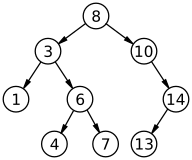
- Корневой узел — самый верхний узел дерева (узел 8 на примере).
- Корень — одна из вершин, по желанию наблюдателя.
- Лист, листовой или терминальный узел — узел, не имеющий дочерних элементов (узлы 1, 4, 7, 13).
- Внутренний узел — любой узел дерева, имеющий потомков, и таким образом, не являющийся листовым узлом (3, 6, 10, 14).
Дерево считается ориентированным, если в корень не заходит ни одно ребро.
- Полный сцепленный ключ — идентификатор записи, который образуется путём конкатенации всех ключей экземпляров родительских записей (групп).
Узлы[править | править код]
Узел является экземпляром одного из двух типов элементов графа, соответствующим объекту некоторой фиксированной природы. Узел может содержать значение, состояние или представление отдельной информационной структуры или самого дерева. Каждый узел дерева имеет ноль или более узлов-потомков, которые располагаются ниже по дереву (по соглашению, деревья "растут" вниз, а не вверх, как это происходит с настоящими деревьями). Узел, имеющий потомка, называется узлом-родителем относительно своего потомка (или узлом-предшественником, или старшим). Каждый узел имеет не больше одного предка. Высота узла — это максимальная длина нисходящего пути от этого узла к самому нижнему узлу (краевому узлу), называемому листом. Высота корневого узла равна высоте всего дерева. Глубина вложенности узла равна длине пути до корневого узла.
Корневые узлы[править | править код]
Узел, не имеющий предков (самый верхний), называется корневым узлом. Это узел, на котором начинается выполнение большинства операций над деревом (хотя некоторые алгоритмы начинают выполнение с «листов» и выполняются, пока не достигнут корня). Все прочие узлы могут быть достигнуты путём перехода от корневого узла по рёбрам (или ссылкам) (согласно формальному определению, каждый подобный путь должен быть уникальным). В диаграммах он обычно изображается на самой вершине. В некоторых деревьях, например, кучах, корневой узел обладает особыми свойствами. Каждый узел дерева можно рассматривать как корневой узел поддерева, «растущего» из этого узла.
Поддеревья[править | править код]
Поддерево — часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева. Любой узел дерева T вместе со всеми его узлами-потомками является поддеревом дерева T. Для любого узла поддерева либо должен быть путь в корневой узел этого поддерева, либо сам узел должен являться корневым. То есть поддерево связано с корневым узлом целым деревом, а отношения поддерева со всеми прочими узлами определяются через понятие соответствующее поддерево (по аналогии с термином «соответствующее подмножество»).
Упорядочивание деревьев[править | править код]
Существует два основных типа деревьев. В рекурсивном дереве или неупорядоченном дереве имеет значение лишь структура самого дерева без учёта порядка потомков для каждого узла. Дерево, в котором задан порядок (например, каждому ребру, ведущему к потомку, присвоены различные натуральные числа) называется деревом с именованными рёбрами или упорядоченным деревом со структурой данных, заданной перед именованием и называемой структурой данных упорядоченного дерева.
Упорядоченные деревья являются наиболее распространёнными среди древовидных структур. Двоичное дерево поиска — одно из разновидностей упорядоченного дерева.
Представление деревьев[править | править код]
Существует множество различных способов представления деревьев. Наиболее общий способ представления изображает узлы как записи, расположенные в динамически выделяемой памяти с указателями на своих потомков, предков (или и тех и других), или как элементы массива, связанные между собой отношениями, определёнными их позициями в массиве (например, двоичная куча).
Деревья как графы[править | править код]
В теории графов дерево — связный ациклический граф. Корневое дерево — это граф с вершиной, выделенной в качестве корневой. В этом случае любые две вершины, связанные ребром, наследуют отношения «родитель-потомок». Несвязный граф, состоящий исключительно из деревьев, называется лесом.
Методы обхода[править | править код]
Пошаговый перебор элементов дерева по связям между узлами-предками и узлами-потомками называется обходом дерева. Зачастую операция может быть выполнена переходом указателя по отдельным узлам. Обход, при котором каждый узел-предок просматривается прежде его потомков, называется предупорядоченным обходом или обходом в прямом порядке (pre-order walk), а когда просматриваются сначала потомки, а потом предки, то обход называется поступорядоченным обходом или обходом в обратном порядке (post-order walk). Существует также симметричный обход, при котором посещается сначала левое поддерево, затем узел, затем — правое поддерево, и обход в ширину, при котором узлы посещаются уровень за уровнем (N-й уровень дерева — множество узлов с высотой N). Каждый уровень обходится слева направо.
Общие операции[править | править код]
- вставка нового элемента в определённую позицию;
- вставка поддерева;
- добавление ветви дерева (называется прививкой);
- нахождение корневого элемента для любого узла;
- нахождение наименьшего общего предка двух вершин;
- перебор всех элементов дерева;
- перебор элементов ветви дерева;
- поиск изоморфного поддерева;
- поиск элемента;
- удаление ветви дерева (называется обрезкой);
- удаление поддерева;
- удаление элемента.
Общее применение[править | править код]
- управление иерархией данных;
- упрощение поиска информации (см. обход дерева);
- управление сортированными списками данных;
- синтаксический разбор арифметических выражений (англ. parsing), оптимизация программ;
- в качестве технологии компоновки цифровых картинок для получения различных визуальных эффектов;
- форма принятия многоэтапного решения (см. деловые шахматы).
См. также[править | править код]
- Двоичное разбиение пространства
- Куча (структура данных)
- Дерево (теория графов)
- Дерево (теория наборов)
- Древовидная структура
- Префиксное дерево
- Экспоненциальное дерево
- Распространённые древовидные структуры
- Прочие деревья
- B-дерево (2-3-дерево, B+-деревья, B*-дерево, UB-дерево)
- DSW-алгоритм
- Танцующее дерево
- Анфилада
- Смешанное дерево
- k-мерное дерево
- Октодерево
- Квадродерево
- R-дерево (структура данных)
- Дерево покрытий
- Дерево остатков
- Сегментное дерево
- Список с пропусками
- T-дерево
- T-пирамида
- Верхнее дерево
- Дерево ван Емде Боаса
- Прошитое двоичное дерево
- Список структур данных (деревья)
Примечания[править | править код]
Литература[править | править код]
- Дональд Э. Кнут. Глава 2.3. Деревья // Искусство программирования = The Art of Computer Programming. — 3-е изд. — М.: Вильямс, 2002. — Т. 1. Основные алгоритмы. — 720 с. — ISBN 5-8459-0080-8 (рус.) ISBN 0-201-89683-4 (англ.).
- Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Introduction to Algorithms. — 2nd Edition. — MIT Press, McGraw-Hill, 2001. — ISBN 0-262-03293-7.
- Section 10.4: Representing rooted trees, pp.214-217.
- Chapters 12-14 (Binary Search Trees, Red-Black Trees, Augmenting Data Structures), pp. 253—320.