Криптографическая хеш-функция
Криптографические хеш-функции — это выделенный класс хеш-функций, который имеет определённые свойства, делающие его пригодным для использования в криптографии.
Принципы построения[править | править код]
Итеративная последовательная схема[править | править код]

В общем случае в основе построения хеш-функции лежит итеративная последовательная схема. Ядром алгоритма является сжимающая функция — преобразование k входных в n выходных бит, где n — разрядность хеш-функции, а k — произвольное число, большее n. При этом сжимающая функция должна удовлетворять всем условиям криптостойкости.
Входной поток разбивается на блоки по (k − n) бит. Алгоритм использует вре́менную переменную размером в n бит, в качестве начального значения которой берётся некое общеизвестное число. Каждый следующий блок данных объединяется с выходным значением сжимающей функции на предыдущей итерации. Значением хеш-функции являются выходные n бит последней итерации. Каждый бит выходного значения хеш-функции зависит от всего входного потока данных и начального значения. Таким образом достигается лавинный эффект.
При проектировании хеш-функций на основе итеративной схемы возникает проблема с размером входного потока данных. Размер входного потока данных должен быть кратен (k − n). Как правило, перед началом алгоритма данные расширяются неким, заранее известным, способом.
Помимо однопроходных алгоритмов, существуют многопроходные алгоритмы, в которых ещё больше усиливается лавинный эффект. В этом случае данные сначала повторяются, а потом расширяются до необходимых размеров.
Сжимающая функция на основе симметричного блочного алгоритма[править | править код]
В качестве сжимающей функции можно использовать симметричный блочный алгоритм шифрования. Для обеспечения большей безопасности можно использовать в качестве ключа блок данных, предназначенный к хешированию на данной итерации, а результат предыдущей сжимающей функции — в качестве входа. Тогда результатом последней итерации будет выход алгоритма. В таком случае безопасность хеш-функции базируется на безопасности используемого алгоритма.
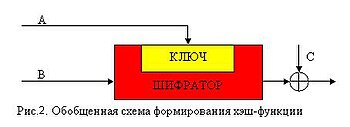
Обычно при построении хеш-функции используют более сложную систему. Обобщённая схема симметричного блочного алгоритма шифрования изображена на рис. 2.
Таким образом, мы получаем 64 варианта построения сжимающей функции. Большинство из них являются либо тривиальными, либо небезопасными. Ниже изображены четыре наиболее безопасные схемы при всех видах атак.

Основным недостатком хеш-функций, спроектированных на основе блочных алгоритмов, является низкая скорость работы. Необходимую криптостойкость можно обеспечить и за меньшее количество операций над входными данными. Существуют более быстрые алгоритмы хеширования, спроектированных самостоятельно, с нуля, исходя из требований криптостойкости. Наиболее распространённые из них — MD5, SHA-1, SHA-2.
Требования[править | править код]
К криптографическим хеш-функциям предъявляются следующие требования:
1. Сопротивление поиску прообраза: при наличии хеша должно быть трудно найти какое-либо сообщение , такое что , Это свойство связано с понятием односторонней функции. Функции, у которых отсутствует это свойство, уязвимы для атак нахождения первого прообраза.
2. Сопротивление поиску второго прообраза: при наличии сообщения , должно быть трудно найти другое сообщение (не равное ) такое, что . Это свойство иногда называют слабым сопротивлением поиску коллизий. Функции, у которых отсутствует это свойство, уязвимы для атак поиска второго прообраза.
3. Стойкость к коллизиям
Коллизией для хеш-функции называется такая пара значений и ′, ′, для которой . Так как количество возможных открытых текстов больше числа возможных значений свёртки, то для некоторой свёртки найдётся много прообразов, а следовательно, коллизии для хеш-функций обязательно существуют. Например, пусть длина хеш-прообраза 6 битов, длина свёртки 4 бита. Тогда число различных свёрток — , а число хеш-прообразов — , то есть в 4 раза больше, значит хотя бы одна свёртка из всех соответствует 4 прообразам.
Стойкость хеш-функции к коллизиям означает, что нет эффективного полиномиального алгоритма, позволяющего находить коллизии.
Данные свойства не являются независимыми:
- Обратимая функция неустойчива к восстановлению второго прообраза и коллизиям.
- Функция, нестойкая к восстановлению второго прообраза, нестойка к коллизиям; обратное неверно.
- Функция устойчивая к коллизиям, устойчива к нахождению второго прообраза.
- Устойчивая к коллизиям хеш-функция не обязательно является односторонней.
Для криптографии важно, чтобы значения хеш-функции сильно изменялись при малейшем изменении аргумента (лавинный эффект). Значение хеша не должно давать утечки информации даже об отдельных битах аргумента.
При разработке современного российского стандарта ГОСТ Р 34.11-2012 (Стрибог) к криптографическим хеш-функциям были сформулированы следующие требования:
- Стойкость к вычислению прообраза: если известно значение функции, тогда должно быть сложно найти такое сообщение, хеш-функция от которого равна известному;
- Стойкость к вычислению второго прообраза: пусть есть одно значение, и известен хеш-код этого значения. Тогда злоумышленнику должно быть сложно найти ещё одно такое значение, чтобы его хеш-функция совпадала с хеш-функцией первого значения;
- Стойкость к поиску коллизий: должно быть сложно найти два таких сообщения, которые не равны, но у них равны хеш-коды;
- Стойкость к удлинению прообраза: если злоумышленник не знает сообщение, но знает его длину и хеш-код от него, то ему должно быть сложно подобрать такое сообщение, которое, будучи дописанным к оригинальному, даст какую-нибудь известную хеш-функцию. Другими словами, не должно быть возможно злоумышленнику что-то менять путём дополнения в сообщении, получая известны выход. Это можно сформулировать по-другому: хеш-функция не должна быть хорошо «дополняема».
4. Псевдослучайность: должно быть трудно отличить генератор псевдослучайных чисел на основе хеш-функции от генератора случайных чисел, например, он проходит обычные тесты на случайность.
Доказуемо безопасные хеш-функции[править | править код]
Безопасность хеш-функции может обеспечиваться сложностью некоторой математической задачи при наличии доказательства, что атаки, направленные на нарушение требований к ней, настолько же сложны, насколько и решение этой задачи.[1]
Криптографическая хеш-функция является доказуемо защищённой от коллизий, если задача нахождения коллизий может быть средуцирована за полиномиальное время[англ.] от задачи , которая считается неразрешимой за полиномиальное время. Иначе говоря, если алгоритм позволял бы за полиномиальное время решить задачу нахождения коллизий при существовании редуцирующего алгоритма , работающего также за полиномиальное время, то последний позволил бы алгоритму решить задачу за полиномиальное время, что противоречит её сложности, а значит задача нахождения коллизий не легче задачи .
Аналогично определяется доказуемая защищённость от поиска первого и второго прообраза.
Стойкость к поиску второго прообраза вытекает из доказанной стойкости к коллизиям, поэтому на практике иногда теоретически доказывается только стойкость к нахождению первого прообраза и стойкость к коллизиям.[2]
Некоторые задачи, полагающиеся неразрешимыми за полиномиальное время, которые могут быть использованы для построения таких функций:
- Дискретное логарифмирование
- Нахождение квадратичного вычета
- Факторизация целых чисел
- Задача о сумме подмножеств
Недостатки доказательного подхода[править | править код]
При наличии теоретических гарантий сложности, у доказательного подхода имеются и существенные недостатки:
- Текущие доказуемо безопасные алгоритмы хеширования слишком вычислительно сложны для того, чтобы использоваться на практике. По сравнению с обычными хеш функциями они достаточно медленные.
- Создание доказуемо безопасных хеш функций значительно более трудоёмко, чем классические подходы.
- Само доказательство безопасности часто основывается на задаче, имеющей требуемую сложность в среднем или в худшем случае. Сложность в худшем случае чаще всего описывает патологические ситуации, а не типичные для этой задачи. Даже редукция к задаче со сложностью в среднем обеспечивает ограниченную защищённость, так как может быть найден алгоритм, который легко решает проблему для определённого подмножества данных задачи. Так, например, было показано, что для двух из трёх предложенных в оригинальной статье для функции Fast Syndrome-Based hash параметров существуют более оптимальные атаки, чем предложенные создателями для доказательства безопасности.[3]
SWIFFT является примером хеш функции, которая несколько обходит описанную проблему безопасности. Может быть показано, что для любого алгоритма, который взламывает SWIFFT с вероятностью за время найдётся алгоритм, который решает определённую математическую задачу в худшем случае за время в зависимости от и .[4]
Примеры доказуемо безопасных хеш-функции[править | править код]
- VSH — Very Smooth Hash function — доказуемо безопасная устойчивая к коллизиям функция, опирающаяся на сложность нахождения нетривиальных квадратных корней по модулю составного числа n (что является настолько же сложным, насколько разложение n на множители).
- MuHASH
- ECOH - Elliptic curve only hash[англ.] — основанная на идее эллиптических кривых, задаче о сумме подмножеств и суммировании полиномов хеш функция. Доказательство безопасности опиралось на предположение о NP-полноте лежащей в основе математической задачи, однако была найдена уязвимость для обобщённой атаки «дней рождения» Вагнера, связанной с поиском второго прообраза.[5]
- FSB — Fast Syndrome-Based hash function — может быть показано, что взломать FSB по меньшей мере настолько же трудно, насколько решить NP-полную задачу, известную как регулярное синдромное декодирование.[6]
- SWIFFT — SWIFFT основан на БПФ и доказуемо безопасен при довольно слабом предположении о сложности нахождения коротких векторов в циклической/идеальной решётке в худшем случае.[7]
- Chaum, van Heijst, Pfitzmann hash function — функция, в которой нахождение коллизий так же трудоёмко, как и при нахождении дискретного логарифма в конечной группе .
- Knapsack-based hash functions — семейство хеш-функций, основанное на задаче о рюкзаке.
- Существует общий подход к построению доказуемо безопасных алгоритмов хеширования на основе любого подходящего сигма протокола[англ.]. Более быстрая версия VSH (называющаяся VSH*) может быть получена таким способом.
Идеальная криптографическая хеш-функция[править | править код]
Идеальной криптографической хеш-функцияей является такая криптографическая хеш-функция, к которой можно отнести пять основных свойств:
- Детерминированность. При одинаковых входных данных результат выполнения хеш-функции будет одинаковым (одно и то же сообщение всегда приводит к одному и тому же хешу);
- Высокая скорость вычисления значения хеш-функции для любого заданного сообщения;
- Невозможность сгенерировать сообщение из его хеш-значения, за исключением попыток создания всех возможных сообщений;
- Наличие лавинного эффекта. Небольшое изменение в сообщениях должно изменить хеш-значения, так широко, что новые хеш-значения не совпадают со старыми хеш-значениями;
- Невозможность найти два разных сообщения с одинаковыми хеш-значениями.
Таким образом, идеальная криптографическая хеш-функция, у которой длина n (то есть на выходе n бит), для вычисления прообраза должна требовать как минимум операций.
Злоумышленник будет искать прообраз для идеальной хеш-функции следующим образом: у него есть число h, и ему надо найти такое m, что H(m) = h. Если это идеальная хеш-функция, то злоумышленнику остаётся лишь перебирать все возможные M и проверять, чему равна хеш-функция от этого сообщения. Результат вычисления, если m перебирается полностью, есть фактически случайное число. Если число h лежит в диапазоне от 0 до , то тогда в среднем на поиски нужного h злоумышленник будет тратить итераций. Таким образом, вычисление прообраза займёт в два раза меньше итераций, чем в идеальном случае.
Вычисление второго прообраза останется . В поиске коллизий оценка даст , причём это не совсем точный результат. Данная оценка идёт из оценки так называемого «Парадокса дней рождения».
Если злоумышленник хочет написать программу по поиску коллизий, ему будет оптимально вначале завести себе словарь коллизий. Соответственно, дальше он вычисляет хеш-функцию от очередного сообщения и проверяет, принадлежит эта хеш-функция очередному сообщению или нет. Если принадлежит, то коллизия найдена, и тогда можно найти по словарю исходное сообщение с данным хеш-кодом. Если нет, то он пополняет словарь. На практике такой способ не реализуется, потому что не хватило бы памяти для подобного словаря.
«Атака дней рождения»[править | править код]
Атака «дней рождения» — используемое в криптоанализе название для метода поиска коллизий хеш-функций на основе парадокса дней рождения. Суть парадокса в том, что в группе, состоящей из 23 или более человек, вероятность совпадения дней рождения (число и месяц) хотя бы у двух людей превышает 50 %. Например, если в классе 23 ученика или более, то более вероятно то, что у кого-то из одноклассников дни рождения придутся на один день, чем то, что у каждого будет свой неповторимый день рождения.
«Лавинный эффект»[править | править код]
Рассмотрим этот эффект и его роль на примере процесса хеширования блокчейна. Это свойство означает, что если мы вносим малые изменения во входную строку, то хеши (то есть output криптографической функции) будут кардинально отличаться друг от друга. Проверим это свойство на простом примере. Рассмотрим, например, результат хеш-функции из семейства MD — MD5. На вход подадим значения, у которых будут отличаться только регистр первых символов — строки практически идентичны. Однако их хеши (результат хеш-функции) различны.
| Пример работы алгоритма шифрования MD5 | |
| Input | Output |
| bitcoin | 0xCD5B1E4947E304476C788CD474FB579A |
| Bitcoin | 0xD023EC040F79F1A9B2AC960B43785089 |
«Высокая энтропия»[править | править код]
Хорошие хеш-функции обладают свойством «Высокой энтропии». Это означает, что хеши массивов данных должны быть максимально распределены в системе в процессе хеширования, то есть обладать высоким показателем энтропии в смысле информации. Как известно, энтропия в смысле информации — мера неопределённости некоторой системы, в частности непредсказуемость появления какого-либо символа.
Так, например, рассмотрим уравнение , где — конкатенация строки и строки , а — криптографическая хеш-функция. Если значение обладает высоким показателем энтропии, то найти такое значение , которое бы удовлетворяло уравнению, будет практически невозможно.
Термин «Высокая энтропия» в контексте хеш-функций означает состояние, при котором значение выбрано из такого широкого круга всевозможных вариантов, что попытки угадывания методом случайного подбора имеют очень низкий шанс на успех. Например, число, которое находится в рамках от 1 до 10, обладает низким показателем энтропии, в то время как число, которое находится в интервале между 1 и , наоборот, имеет высокий показатель энтропии.
Семейство хеш-функций MD и SHA[править | править код]
На сегодняшний день подавляющую долю применений хеш-функций «берут на себя» алгоритмы MD5, SHA-1, SHA-256, а в России — ещё и ГОСТ Р 34.11-2012 (Стрибог). Конечно, существует и множество других менее известных или распространённых только в узких сообществах алгоритмов (например, RIPEMD, TIGER, Panama и др.), однако, эти алгоритмы не так распространены. Ниже представлен анализ хеш-функций MD4, которая была предшественником MD5, а также хеш-функции SHA.
| Тип | Описание |
|---|---|
| MD4 | Самая быстрая, оптимизирована для 32-битных машин среди семейства MD-функций.
Хеш-функция, разработанная профессором Массачусетского университета Рональдом Ривестом в 1990 году и впервые описанная в RFC 1186. Содержит три цикла по 16 шагов каждый. В 1993 году был описан алгоритм взлома MD4, поэтому на сегодняшний день данная функция не рекомендована для использования с реальными приложениями. |
| MD5 | Наиболее распространённая из семейства MD-функций. Похожа на MD4, но средства повышения безопасности делают её на 33 % медленнее, чем MD4. Содержит четыре цикла по 16 шагов каждый. Обеспечивает контроль целостности данных.
Первые успешные попытки взлома данной хеш-функции датируются 1993 годом: исследователи Берт ден Боер и Антон Боссиларис показали, что в алгоритме возможны псевдоколлизии. В 1996 году Ганс Доббертин показал наличие возможности коллизий и теоретически описал алгоритм взлома. 24 августа 2004 года четыре независимых исследователя — Ван Сяоюнь, Фэн Дэнгуо, Лай Сюэцзя и Юй Хунбо — обнаружили уязвимость алгоритма, позволяющую найти коллизии аналитическим методом за более-менее приемлемое время. В 2005 году Властимил Клима опубликовал алгоритм, позволяющий обнаруживать коллизии за несколько часов. Восемнадцатого марта 2006 года исследователь обнародовал алгоритм, находящий коллизии за одну минуту, который позднее получил название «туннелирование». На сегодняшний день MD5 не рекомендована для использования в реальных приложениях. |
| SHA-1
(Secure Hash Algorithm 1) |
В 1993 году NSA совместно с NIST разработали алгоритм безопасного хеширования (сейчас известный как SHA-0) (опубликован в документе FIPS PUB 180) для стандарта безопасного хеширования. Однако вскоре NSA отозвало данную версию, сославшись на обнаруженную ими ошибку, которая так и не была раскрыта. И заменило его исправленной версией, опубликованной в 1995 году в документе FIPS PUB 180-1. Эта версия и считается тем, что называют SHA-1.
Позже, на конференции CRYPTO в 1998 году два французских исследователя представили атаку на алгоритм SHA-0, которая не работала на алгоритме SHA-1. Возможно, это и была ошибка, открытая NSA. SHA-1 создаёт 160-битное значение, называемое также дайджестом сообщения. Содержит четыре этапа. И MD5, и SHA-1 являются, по сути, улучшенными продолжениями MD4. Различия:
|
| SHA-2 | Семейство криптографических алгоритмов — хеш-функций, включающее в себя алгоритмы SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/256 и SHA-512/224.
В 2003 году Гилберт и Хандшух провели исследование SHA-2, но не нашли каких-либо уязвимостей. Однако в марте 2008 года индийские исследователи Сомитра Кумар Санадия и Палаш Саркар опубликовали найденные ими коллизии для 22 итераций SHA-256 и SHA-512. В сентябре того же года они представили метод конструирования коллизий для усечённых вариантов SHA-2 (21 итерация). Как показали исследования[8], алгоритмы SHA-2 работают в 2—3 раза медленнее хеш-алгоритмов MD5, SHA-1. |
| SHA-256 | Отдельно выделяется алгоритм SHA-256, который применяется в алгоритмах хеширования биткойна и других криптовалют. Как понятно из названия криптографической хеш-функции, выходной хеш составляет в длину 256 бит, соответствующую энтропию можно определить как множество значений от 1 до 2 в степени 256 — огромное число значений, что делает взлом и расшифровку крайне трудоёмким процессом, опирающимся на последовательный перебор. |
| SHA-3 (Keccak) | Хеш-функция SHA-3 (также называемая Keccak) является функцией переменной разрядности, разработанная группой авторов во главе с Йоаном Дайменом. 2 октября 2012 года Keccak стала победителем конкурса криптографических алгоритмов, проводимым Национальным институтом стандартов и технологий США[9]. 5 августа 2015 года алгоритм функции был утверждён и опубликован в качестве стандарта FIPS 202[10][11]. Алгоритм функции SHA-3 построен по принципу криптографической губки. |
Применения[править | править код]
Электронная подпись[править | править код]
Чтобы убедиться, что сообщение отправил конкретный отправитель, вместе с сообщением передаётся так называемая электронная подпись. Получатель проверяет, действительно ли электронная подпись относится к данному сообщению.
В связи с тем, что использование криптографии с открытыми ключами (подписывание, проверка подписей и т. д.) — процесс очень медленный, более того, если подписывать всё сообщение целиком, то размеры этой подписи будут сопоставимы с размером сообщения, подписывают не сообщение, а хеш-функцию от сообщения. И далее получатель, когда расшифровывает подпись, получает хеш-функцию. Далее он сравнивает хеш-функцию от того сообщения, которое он получил, и хеш-функцию, которая была получена в результате расшифровки. За счёт того, что хеш-функция имеет фиксированную длину, она меньше, чем само сообщение. Это позволяет быстро вычислить электронную подпись. Размер этой подписи будет мал по сравнению с размером сообщения.
Проверка парольной фразы[править | править код]
В большинстве случаев парольные фразы не хранятся на целевых объектах, хранятся лишь их хеш-значения. Хранить парольные фразы нецелесообразно, так как в случае несанкционированного доступа к файлу с фразами злоумышленник узнает все парольные фразы и сразу сможет ими воспользоваться, а при хранении хеш-значений он узнает лишь хеш-значения, которые не обратимы в исходные данные, в данном случае — в парольную фразу. В ходе процедуры аутентификации вычисляется хеш-значение введённой парольной фразы и сравнивается с сохранённым.
Примером в данном случае могут служить ОС GNU/Linux и Microsoft Windows XP. В них хранятся лишь хеш-значения парольных фраз из учётных записей пользователей.
Данная система подразумевает передачу сообщения по защищённому каналу, то есть каналу, из которого криптоаналитику невозможно перехватить сообщения или послать своё. Иначе он может перехватить парольную фразу, и использовать её для дальнейшей нелегальной аутентификации. Защищаться от подобных атак можно при помощи метода «вызов-ответ».
Пусть некий клиент, с именем name, производит аутентификацию по парольной фразе, pass, на некоем сервере. На сервере хранится значение хеш-функции H(pass, R2), где R2 — псевдослучайное, заранее выбранное число. Клиент посылает запрос (name, R1), где R1 — псевдослучайное, каждый раз новое число. В ответ сервер посылает значение R2. Клиент вычисляет значение хеш-функции H(R1, H(pass, R2)) и посылает его на сервер. Сервер также вычисляет значение H(R1, H(pass, R2)) и сверяет его с полученным. Если значения совпадают — аутентификация верна.
В такой ситуации пароль не хранится открыто на сервере и, даже перехватив все сообщения между клиентом и сервером, криптоаналитик не может восстановить пароль, а передаваемое хеш-значение каждый раз разное.
Хеширование биткойна[править | править код]
Транзакции платёжной системы Биткойна, которые представляются в виде некоторого массива данных, объединяются в блоки (в дальнейшем, совокупность всех блоков будем называть блокчейном) и проходят через алгоритм хеширования, то есть данные их полей подаются на вход криптографической хеш-функции. Каждая транзакция указывает, откуда списываются средства и куда они направляются. Для указания адресата используется его публичный ключ (уникальный идентификатор в сети биткойн). Чтобы адресат мог использовать полученные деньги в рамках протокола биткойна (исключаем продажу собственного кошелька — Wallet), он должен создать новую транзакцию, которая будет брать валюту с предыдущей и перенаправлять по другому адресу, используя публичный ключ. Соответственно, новая транзакция вместе с транзакциями других пользователей сети биткойн попадёт в новый блок. Таким образом число блоков в блокчейне растёт. Однако, каждая транзакция должна быть одобрена — система должна прийти к консенсусу. Для этого есть несколько способов, но в биткойне используется принцип Proof-of-Work (PoW). После принятия транзакции она считается настоящей и криптовалюта переходит от одного кошелька к другому.
Система биткойна является децентрализованной системой без выделенных центров генерации блоков. Каждый участник может взять набор транзакций, ожидающих включения в журнал, и сформировать новый блок. Более того, в системах типа BitCoin такой участник (майнер) ещё и получит премию в виде определённой суммы или комиссионных от принятых в блок транзакций.
Но нельзя просто так взять и сформировать блок в децентрализованных системах. Система должна прийти к консенсусу, то есть получить одобрение. Для этого есть несколько способов, но в биткойне используется принцип Proof-of-Work (PoW). Надёжность таких систем основывается именно на том, что новый блок нельзя сформировать быстрее (в среднем), чем за определённое время. Например, за 10 минут (BitCoin).
| Field | Description | Size |
|---|---|---|
| Magic no | value always 0xD9B4BEF9 | 4 bytes |
| Blocksize | number of bytes following up to end of block | 4 bytes |
| Blockheader | consist of 6 items | 80 bytes |
| Transaction counter | positive integer | 1-4 bytes |
| transactions | the <non empty> list of transactions | <Transaction counter> — many transactions |
| Field | Purpose | Update when… | Size |
|---|---|---|---|
| Version | Block version number | You upgrade software and it specified new version | 4 |
| hashPrevBlock | 256-bit hash of the previous block header | A new block comes in | 32 |
| hashMerkelRoot | 256-bit hash based on all of the transactions in the block | A transaction is accepted | 32 |
| Time | current timestamp as seconds since 1970-01-01 T00:00 UTC | Every few seconds | 4 |
| Bits | current target in compact format | The difficulty is adjusted | 4 |
| Nonce | 32-bit number (starts at 0) | A hash is tired (increments) | 4 |
difficulty — количество нулевых бит, которые будут в начале числа target.
target — число, меньше которого должен быть хеш блока, чтобы блок считался верным. Target или, точнее, difficulty зависит от текущей мощности сети и нужно менять сложность каждые n (в сети BitCoin — 2016) блоков, для того, чтобы один блок генерировался раз в 10 минут. Предположим, что в сети генерируется 2016 блоков, и каждый клиент проверяет, за какое время создавался каждый блок. Если это время больше, чем рассчитывалось, то есть больше 10 минут, то сложность уменьшается.
nonce — случайное число, которое нужно подобрать майнерам для того, чтобы составить блок.
Устройство структуры данных биткойна[править | править код]
Как уже говорилось выше, набор транзакций Биткойна представляются в виде связанных блоков данных — блокчейн. Структура устройства самого блокчейна представлена в виде связанного списка с указателями.
Каждый блок имеет указатель, который содержит ссылку на предыдущий блок данных. Таким образом, для того, чтобы перейти к n + 1 блоку, необходимо пройти по указателям предыдущих n блоков. Соответственно, указатели добавляют адрес нового блока только после прохождения исходного блока данных через алгоритм хеширования биткойна — это позволяет сделать связь надёжной и защищённой.
Такая система уязвима с малой вероятностью перед атаками злоумышленников, которые могут попытаться изменить данные в блокчейне, например, для осуществления собственной транзакции по выбранном адресу. Как уже говорилось, хеш каждого блока в блокчейне зависит не только от его собственного содержания, но и от содержания предыдущего блока. Таким образом, любое изменение данных в исходном блоке влечёт за собой изменение данных в других блоках. Это гарантирует неизменность блокчейна и безопасность системы, так как «подделать» блокчейн оказывается крайне тяжело. Однако, следует заметить, что хеш у каждого блока должен быть уникальным, иначе отслеживание покушений на атаку станет невозможным.
Дерево Меркла[править | править код]
Все транзакции представлены как строки в шестнадцатеричном формате, которые хешируются для получения идентификаторов транзакций. На их основе строится хеш блока, который учитывается последующим блоком, обеспечивая неизменяемость и связность. Единое хеш-значение блока собирается при помощи дерева Меркла.
Дерево Меркла — полное двоичное дерево, в листовые вершины которого помещены хеши от транзакций, а внутренние вершины содержат хеши от сложения значений в дочерних вершинах, а корневой узел дерева (Top Hash) содержит хеш от всего набора данных.

Построение дерева Меркла для блокчейна биткойна происходит следующим образом:
— результат хеш-функции от транзакции
- Вычисляются хеши транзакций, размещённых в блоках: H(L1), H(L2), H(L3) и так далее.
- Вычисляются хеши от суммы хешей транзакций, например H(H(L1) + H(L2)). Так как дерево Меркла является бинарным, то число элементов на каждой итерации должно быть чётным. Поэтому если блок содержит нечётное количество транзакций, то последняя дублируется и складывается сама с собой: hash (H(L3) + H(L3)).
- Далее, вновь вычисляются хеши от суммы хешей. Процесс повторяется, пока не будет получен единый хеш — корень дерева Меркла. Он является криптографическим доказательством целостности блока (то есть того, что все транзакции находятся в заявленном порядке). Значение корня фиксируется в заголовке блока.
При этом, когда, транзакция L1, например, будет потрачена, то данные о ней можно удалить из блока и оставить только её хеш для верификации блока. Когда будут потрачены транзакций L1 и L2, то тогда мы можем удалить и их хеши (Hash 0-0 и Hash 0-1), оставив только Hash 0, опять же в целях верификации блока. В момент, когда все транзакции окажутся использованными, тогда можно удалить все хеши, кроме Top Hash, потому что информация об этих транзакциях будет больше не нужна.
Таким образом, для того, чтобы получить хеш для нового блока цепочки, необходимо учесть все предыдущие хеши транзакций. Изменение хеша хотя бы одного из предыдущих блоков будет вести за собой изменение хеша следующего блока, соответственно, такую транзакцию можно будет сразу определить как невалидную.
Майнинг биткойна[править | править код]
Майнинг — это процесс поиска консенсуса по принципу Proof-Of-Work — получение одобрения на создание нового блока. Фактически в сети BitCoin это сводится к подсчёту хеша от блока и сравнением его с числом target: если хеш оказывается меньше target, то генерируется новый блок, в противном случае — нет.
Майнеры обеспечивают беспрерывный рост блокчейна. Для этого используются огромные вычислительные мощности — каждый майнер делает свой вклад в увеличение общего хешрейта биткоина (вычислительной мощности) . От показателя общего хешрейта зависит удельный вес операции хеширования биткойна каждым майнером — чем выше общий хешрейт сети, тем больший объём вычислительной работы за меньшее количество времени должен сделать майнер, чтобы сохранить средний размер своего вознаграждения за майнинг.
Процесс подстановки nonce в строку длится до тех пор, пока не будет найдено верное решение. Иногда количество попыток может доходить до миллионов раз. Тот майнер, который первым найдёт верное решение, добавляет блок в блокчейн и получает за это вознаграждение.
Процесс подбора nonce основан на применении метода brute force. Поэтому майнинговое оборудование непрерывно генерирует случайные строки до тех пор, пока не будет найдено необходимое значение nonce.
Примеры криптовалют, которые используют хеш-функцию SHA-256 для шифрования[править | править код]
SHA—256 — это классический алгоритм для криптовалют: на нём построена основная криптовалюта — Bitcoin. Соответственно, и в форках биткоина используется этот алгоритм: в Bitcoin Cash, Bitcoin SV. В то же время, в Bitcoin Gold майнеры используют криптофункцию - Equihash
Помимо них, SHA—256 используется также в:
Также алгоритм SHA-256 используется как подпрограмма в криптовалюте Litecoin, а основным алгоритмом для майнинга её является Scrypt.
См. также[править | править код]
Примечания[править | править код]
- ↑ Daniel Augot, Matthieu Finiasz, Nicolas Sendrier. A Fast Provably Secure Cryptographic Hash Function. — 2003. — № 230. — С. 3—4. Архивировано 8 декабря 2019 года.
- ↑ Daniel Augot, Matthieu Finiasz, Nicolas Sendrier. A Fast Provably Secure Cryptographic Hash Function. — 2003. — № 230. — С. 3. Архивировано 8 декабря 2019 года.
- ↑ Jean-Sebastien Coron, Antoine Joux. Cryptanalysis of a Provably Secure Cryptographic Hash Function. — 2004. — № 013. — С. 1,3. Архивировано 7 декабря 2019 года.
- ↑ Alon Rosen, Chris Peikert, Daniele Micciancio, Vadim Lyubashevsky. SWIFFT: A Modest Proposal for FFT Hashing (англ.) // Fast Software Encryption. — Springer, Berlin, Heidelberg, 2008-02-10. — P. 65. — ISBN 9783540710387, 9783540710394. — doi:10.1007/978-3-540-71039-4_4. Архивировано 8 апреля 2019 года.
- ↑ Michael A. Halcrow, Niels Ferguson. A Second Pre-image Attack Against Elliptic Curve Only Hash (ECOH). — 2009. — № 168. Архивировано 24 декабря 2018 года.
- ↑ Daniel Augot, Matthieu Finiasz, Nicolas Sendrier. A Fast Provably Secure Cryptographic Hash Function. — 2003. — № 230. Архивировано 8 декабря 2019 года.
- ↑ Alon Rosen, Chris Peikert, Daniele Micciancio, Vadim Lyubashevsky. SWIFFT: A Modest Proposal for FFT Hashing (англ.) // Fast Software Encryption. — Springer, Berlin, Heidelberg, 2008-02-10. — P. 54—72. — ISBN 9783540710387, 9783540710394. — doi:10.1007/978-3-540-71039-4_4. Архивировано 8 апреля 2019 года.
- ↑ Speed Comparison of Popular Crypto Algorithms (англ.). www.cryptopp.com. Дата обращения: 22 декабря 2017. Архивировано 2 июля 2017 года.
- ↑ Swenson, Gayle (2012-10-02). "NIST Selects Winner of Secure Hash Algorithm (SHA-3) Competition". NIST (англ.). Архивировано 5 октября 2012. Дата обращения: 23 декабря 2017.
- ↑ Hernandez, Paul (2015-08-05). "NIST Releases SHA-3 Cryptographic Hash Standard". NIST (англ.). Архивировано 24 января 2018. Дата обращения: 23 декабря 2017.
- ↑ Morris J. Dworkin. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions (англ.) // Federal Inf. Process. Stds. (NIST FIPS) - 202. — 2015-08-04. Архивировано 17 сентября 2017 года.
Литература[править | править код]
- Брюс Шнайер. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. — М.: Триумф, 2002. — ISBN 5-89392-055-4.
- Лапонина О.Р. Криптографические основы безопасности. — М.: Интернет-университет информационных технологий - ИНТУИТ.ру, 2004. — С. 320. — ISBN 5-9556-00020-5.
Ссылки[править | править код]
- Информация по электронной цифровой подписи.
- Хеш-функция Keccak и конструкция Sponge как универсальный криптопримитив, pgpru.com, 2010—2013 (перевод материала с noekon.org)
- Текст официального стандарта ГОСТ Р 34.11-2012 в Викитеке
Для улучшения этой статьи желательно:
|































