Эллиптическая кривая

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

Эллипти́ческая крива́я — это множество точек, удовлетворяющих уравнению

y^2+a_1 xy+a_3 y=x^3+a_2 x^2+a_4 x+a_6 ~

и плюс точка на бесконечности.

Если характеристика поля (\operatorname{Char}\,K), над которым рассматривается данное уравнение, не равна 2 или 3, то уравнение с помощью замены координат приводится к канонической форме (форме Вейерштрасса):

y2 = x3 + ax + b.

Если \operatorname{Char}\,K=3, то каноническим видом уравнения является вид

y^2=x^3+a_2 x^2+a_4 x+a_6 ~.

А если \operatorname{Char}\,K=2, то уравнение приводится одному из видов:

y^2+y=x^3+ax+b~ - суперсингулярные кривые

или

y^2+xy=x^3+ax^2+b~ - несуперсингулярные кривые.

Эллиптические кривые являются одним из основных направлений в современной теории чисел. Например, они были использованы Эндрю Уайлзом (совместно Ричардом Тейлором) в доказательстве Великой теоремы Ферма. Они примененяются в криптографии (см. Эллиптическая криптография). В частности, на эллиптических кривых основан российский стандарт цифровой подписи ‎ГОСТ Р 34.10-2001. Кроме того, эллиптические кривые применяются при факторизации (см. Алгоритм Ленстры).

Эллиптическая кривая вовсе не то же самое, что эллипс: см. эллиптический интеграл о происхождении термина.

Содержание

[править] Эллиптические кривые над действительными числами

Формальное определение эллиптической кривой трудно для понимания и требует некоторых знаний в алгебраической геометрии. Попробуем описать некоторые свойства эллиптических кривых над действительными числами, используя только знания алгебры и геометрии старших классов школы.

Считаем, что характеристика поля — не 2 и 3. Тогда эллиптическая кривая — плоская кривая, определённая уравнением вида

y^2 = x^3 + ax + b~,

где a и b — действительные числа. Этот вид уравнений называется уравнениями Вейерштрасса.

Например, на следующем чертеже показаны эллиптические кривые, определённые уравнениями y^2 = x^3 - x~ и y^2 = x^3 - x + 1~. Изображение:ECexamples01.png

По определению, необходимо, чтобы такая кривая не имела особых точек. Геометрически это значит, что график не должен иметь точек возврата и самопересечений. Алгебраически это значит, что дискриминант

\Delta = -16(4a^3 + 27b^2)~

не должен быть равен нулю.

Если кривая не имеет особых точек, то её график имеет две части, если дискриминант положителен, и одну — если отрицателен. Например, для графиков выше в первом случае дискриминант равен 64, а во втором он равен −368.

[править] Групповой закон

Добавив «несобственную точку», мы получим проективный вариант этой кривой. Если P~ и Q~ — две точки на кривой, то мы можем единственным образом описать третью точку — точку пересечения данной кривой с прямой, проведённой через P и Q. Если прямая является касательной к кривой в точке, то такая точка считается дважды. Если прямая параллельна оси Oy, третьей точкой будет несобственная точка (точка, удалённая в бесконечность).

Изображение:ECClines.svg

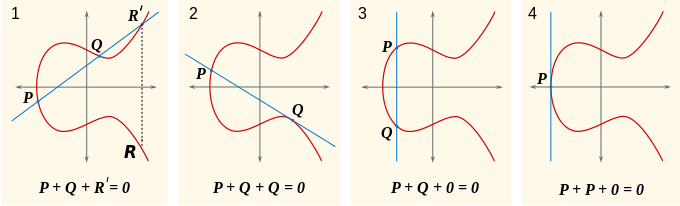
Тогда мы можем ввести групповую операцию «+» на прямой со следующими свойствами: положим, что несобственная точка является нулём группы; и если прямая пересекает данную кривую в точках P, Q и R, то необходимо, чтобы P+Q+R=0~ в группе. Можно показать, что таким образом кривая превращается в абелеву группу, то есть, в абелево многообразие. Можно также показать, что множество K-рациональных точек (включая несобственную) образует подгруппу этой группы. Если кривую обозначить E, то такая подгруппа обычно обозначается как E(K).

Описанная группа может быть описана и алгебраически. Пусть дана кривая y2 = x3 − px − q над полем K (чья характеристика не равна ни 2, ни 3), и точки P = (xP,yP) и Q = (xQ,yQ) на кривой, допустим, что x_P\ne x_Q. Пусть s=\frac{y_P-y_Q}{x_P-x_Q}~; так как K — поле, то s чётко определено. Тогда мы можем определить R=P+Q=(x_R,y_R)~ следующим образом:

x_R = s^2 - x_P - x_Q~,
y_R = -y_P + s(x_P - x_R)~.

Если xP = xQ, то у нас два варианта: если yP = − yQ, то сумма определена как 0; значит, обратную точку к любой точке на кривой можно найти, отразив её по оси Ox. Если y_P=y_Q\ne 0, то R = P + P = 2P = (xR,yR) определяется так:

s = \frac{3x_P^2 - p}{2y_P},
xR = s2 − 2xP,
yR = − yP + s(xP − xR).

Если yP = yQ = 0, то P + P = 0.

[править] Эллиптические кривые над полем комплексных чисел

Формулировка эллиптических кривых как вложения тора в комплексную проективную плоскость следует напрямую из любопытного свойства эллиптических функций Вейерштрасса. Эти функции и их первые производные связаны формулой

\wp'(z)^2 = 4\wp(z)^3 -g_2\wp(z) - g_3.

Здесь g2 и g3 — константы; \wp(z) — эллиптическая функция Вейерштрасса, а \wp'(z) — её производная. Видно, что соотношение — в виде эллиптической кривой (над комплексными числами). Функции Вейерштрасса дважды периодичны; то есть, они являются периодом в отношении структуры Λ по сути, функции Вейерштрасса натурально определены на торе T=\mathbb{C}/\Lambda. Этот тор может быть вложен в комплексную проективную плоскость отображением

z\to (1,\wp(z), \wp'(z)).

Это отображение — групповой изоморфизм, отображающий структуру натуральной группы тора в проективную плоскость. Кроме того, это изоморфизм поверхностей Римана, то есть, топологически, данную эллиптическую кривую можно рассмотреть как тор. Если структура Λ связана со структурой cΛ умножением на ненулевое комплексное число c, то соответствующие кривые изоморфны. Классы изоморфизма эллиптических кривых определены j-инвариантом.

Классы изоморфизма можно рассмотреть более простым способом. Константы g2 и g3, называемые модулярными инвариантами, единственным образом определены структурой тора. Впрочем, комплексные числа являются полем разложения для многочленов, а значит, эллиптические кривые можно записать как

y2 = x(x − 1)(x − λ).

Можно показать, что

g_2 = \frac{4^{1/3}}{3} (\lambda^2-\lambda+1)

и

g_3=\frac{1}{27} (\lambda+1)(2\lambda^2-5\lambda+2),

так что дискриминант модуляра равен

\Delta = g_2^3-27g_3^2 = \lambda^2(\lambda-1)^2.

Здесь λ иногда называют лямбда-функцией модуляра.

Отметим, что теорема об униформизации утверждает, что любая компактная поверхность Римана рода 1 может быть представлена в виде тора.

[править] Эллиптические кривые над произвольным полем

Эллиптические кривые могут быть определены над любым полем K; формально, эллиптическая кривая определяется как невырожденная проективная алгебраическая кривая над K с родом 1 с данной точкой, определённой над K.

Если характеристика поля K не равна 2 или 3, то любая эллиптическая кривая над K может быть записана в виде

y2 = x3 − px − q,

где p и q — такие элементы K, что многочлен x3 − px − q (правая сторона) не имеет кратных корней. (Если характеристика равна 2 или 3, то необходимо ввести ещё несколько условий.)

Можно взять кривую как множество всех точек (x;y), которые удовлетворяют вышеуказанному уравнению, а x и y одновременно являются элементами алгебраического замыкания поля K. Точки кривой, обе координаты которых принадлежат K, называются K-рациональными точками.

[править] Связь с теорией чисел

Теорема Морделла-Вейля утверждает, что если поле K — поле рациональных чисел (или, вообще, поле чисел), то группа K-рациональных точек — конечно порождённая. Это означает, что группа может быть выражена как прямая сумма свободной абелевой группы и конечной подгруппы кручения. Хотя и относительно легко определить подгруппу кручения E(K), но нет общего алгоритма для вычисления ранга свободной подгруппы. Формула для вычисления ранга даётся в гипотезе Бирча и Свиннертона-Дайера.

Недавнее доказательство Великой теоремы Ферма было сделано с помощью доказательства особого случая теоремы Таниямы — Шимуры, относящей эллиптические кривые над рациональными числами к модулярным формам; эта теорема недавно была доказана и в целом.

Точное число рациональных точек эллиптической кривой E над конечным полем \mathbb{F}_p достаточно трудно вычислить, но теорема Хассе об эллиптических кривых утверждает, что

\left| \sharp E( \mathbb{F}_p ) - p - 1 \right| < 2 \sqrt{p} .

Этот факт можно истолковать и доказать с помощью некоторых общих тем; см. Локальная дзета-функция, Этальная когомология. Число точек на данной кривой может быть вычислено с помощью алгоритма Шуфа.

Дальнейшие рассуждения по теме см. в статье Арифметика абелевых многообразий.

[править] Алгоритмы, использующие эллиптические кривые

Эллиптические кривые над конечными полями используются в некоторых криптографических приложениях и факторизации. Обычно, основная идея, заложенная в этих приложениях, заключается в том, что известный алгоритм, используемый для конкретных конечных групп переписывается для использования групп рациональных точек эллиптических кривых. Подробнее см.:

[править] Список литературы

  • Н. Коблиц Курс теории чисел и криптографии = A Course in Number Theory and Cryptography. — Москва: Научное издательство "ТВП", 2001. — С. 254. — ISBN 5-85484-014-6
  • Н. Коблиц Введение в эллиптические кривые и модулярные формы = Introduction to Elliptic Curves and Modular Forms. — Новокузнецк: ИО НФМИ, 2000. — С. 312. — ISBN 5-8032-3325-0
  • С. Ленг Эллиптические функции = Elliptic functions. — Новокузнецк: ИО НФМИ, 2000. — С. 312. — ISBN 5-8032-3326-9
  • Joseph H. Silverman The Arithmetic of Elliptic Curves. — New York: Springer, 1986. — С. 402. — ISBN 0-387-96203-4


[править] Внешние ссылки

Источник — «http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%BB%D0%B8%D0%BF%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BA%D1%80%D0%B8%D0%B2%D0%B0%D1%8F»