Проективный модуль

Материал из Википедии — свободной энциклопедии

Проекти́вный мо́дуль — одно из основных понятий гомологической алгебры. С точки зрения теории категорий, проективные модули являются частным случаем проективных объектов.

Содержание

1 Определение
2 Свойства
3 См. также
4 Литература

[править] Определение

Модуль $P$ над кольцом $A$ (как правило, считаемым ассоциативным c единичным элементом), называется проективным, если для всякого гомоморфизма $g\colon P\to M$ и эпиморфизма $f\colon N\to M$ существует такой гомоморфизм $h\colon P\to N$ , что $g = f h$ , то есть данная диаграмма коммутативна:

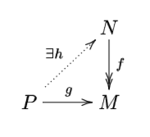
Простейший пример проективного модуля — свободный модуль $F$ . В самом деле, пусть $x_1, x_2, \ldots, x_i,\ldots$ — элементы базиса модуля $F$ и $f (x i) = y i$ для некоторых $y$ из $C$ . Поскольку $g$ — эпиморфизм, можно найти такие $z i$ , что $g (z i) = y i$ . Тогда $h$ определяется своими значениями на векторах базиса $x (x i) = z i$ .

Для колец многочленов от нескольких переменных над полем любой проективный модуль является свободным.

В общем случае это не так, хотя легко доказать теорему о том, что модуль $P$ проективен тогда и только тогда, когда существует такой модуль $K$ , что прямая сумма $F = P \oplus K$ свободна. В самом деле, если $P$ есть компонента прямой суммы $F$ , которая является свободным модулем, и $g\colon P\to M$ — гомоморфизм, то $fp_1 \colon F\to C$ тоже гомоморфизм ( $p 1$ — проекция прямой суммы $F$ на первое слагаемое $P$ ), а так как проективность свободных модулей нам известна, то существует гомоморфизм $h_1\colon F\to N$ , такой, что $g p 1 = f h 1$ , отсюда $g p 1 i 1 = f h 1 i 1$ , где $i 1$ — гомоморфизм включения $P\to F$ , отсюда

$g = fh_1 i_1\colon P\to M$

Обратно, пусть $P$ — проективный модуль. Каждый модуль является гомоморфным образом свободного. Пусть $g\colon F\to P$ — соответствующий эпиморфизм. Тогда тождественный изоморфизм $id\colon P\to P$ будет равен $i d = g h$ для некоторого $h\colon P\to F$ , так как $P$ проективен. Любой элемент $F$ тогда представим в виде

$x = hg(x) + (x-hg(x)) \in \mathrm{Im}\,h \oplus \mathrm{Ker}\,g$ ,

где $\mathrm{Im}\,h$ изоморфно $P$ .

[править] Свойства

$P$ проективен тогда и только тогда, когда для любого эпиморфизма $f\colon N\to M$ индуцированный гомоморфизм $f_* \colon Hom(P,N) \to Hom(P,M)$ является эпиморфизмом.
$P$ проективен тогда и только тогда, когда он переводит любую короткую точную последовательность $0\to A \to B \to C \to 0$ в точную последовательность $0\to Hom(P,A) \to Hom(P,B) \to Hom(P,C) \to 0$ .
Прямая сумма модулей проективна тогда и только тогда, когда проективно каждое слагаемое.