Эффект Джоуля — Томсона

Статистическая физика

$S = k_B \, \ln\Omega$

Термодинамика Молекулярно-кинетическая теория

Статистики Максвелла-Больцмана Бозе-Эйнштейна · Ферми-Дирака Parastatistics · Энионная статистика Braid statistics Ансамбли Микроканонический · Канонический Большой канонический Изотермо-изобарический Изоэнатльпи-изобарический Открытый Термодинамика Уравнение состояния · Цикл Карно · Закон Дюлонга — Пти Модели Модель Дебая · Эйнштейна · Модель Изинга Потенциалы Внутренняя энергия · Энтальпия Свободная энергия Гельмгольца потенциал Гиббса · Большой термодинамический потенциал Известные учёные Максвелл · Гиббс · Больцман

См. также: Портал:Физика

Эффе́ктом Джо́уля — То́мсона называется изменение температуры газа при адиабатическом дросселировании — медленном протекании газа под действием постоянного перепада давлений сквозь дроссель (пористую перегородку). Данный эффект является одним из методов получения низких температур.

Изменение энергии

Изменение энергии газа в ходе этого процесса будет равно работе: $U_2-U_1=P_1V_1-P_2V_2\$. Следовательно, из определения энтальпии ($H=U+PV\$) следует, что процесс изоэнтальпиен.

Изменение температуры

Изменение температуры при малом изменении давления (дифференциальный эффект) в результате процесса Джоуля — Томсона определяется производной $\mu_{JT}=\left(\frac{\partial T}{\partial P}\right)_H$, называемой коэффициентом Джоуля — Томсона. С помощью элементарных преобразований можно получить выражение для этого коэффициента:

$\mu_{JT}=\left(\frac{\partial T}{\partial P}\right)_H=\frac{1}{C_P}\left[T\left(\frac{\partial V}{\partial T}\right)_P-V\right],$

где $C_p\$ — теплоёмкость при постоянном давлении. Для идеального газа $\mu_{JT}=0\$, а для реального газа он определяется уравнением состояния.

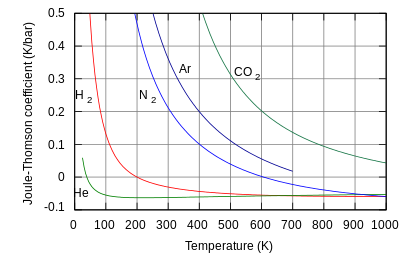
Если при протекании газа через пористую перегородку температура возрастает ($\mu_{JT}<0\$), то эффект называют отрицательным, и наоборот, если температура убывает ($\mu_{JT}>0\$), то процесс называют положительным. Температуру, при которой $\mu_{JT}\$ меняет знак, называют температурой инверсии.

Применение

• Процесс Джоуля — Томсона используют для получения низких температур. Для этой цели обычно применяют интегральный процесс, при котором давление изменяется в широких пределах.
• Измерение $\mu_{JT}\$ позволяет установить уравнение состояния газа.

См. также

• Дросселирование

Литература

• Ландау, Л. Д., Лифшиц, Е. М. Статистическая физика. Часть 1. — Издание 4-е. — М.: Наука, 1995. — («Теоретическая физика», том V).