Энтальпия
| Энтальпия | |
|---|---|
| Размерность | |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| Внесистемные единицы: калория, британская тепловая единица | |
Энтальпи́я (от др.-греч. ενθαλπω — «нагреваю», также теплова́я фу́нкция[1][2], теплова́я фу́нкция Гиббса[3], теплосодержа́ние[1][3] и изобарно-изоэнтропийный потенциал[4]) — функция состояния термодинамической системы, определяемая как сумма внутренней энергии и произведения давления на объём [1][5][6][K 1]:
(Определение энтальпии)
Из уравнения для дифференциала внутренней энергии[9][10]:
(Дифференциал внутренней энергии)
где — термодинамическая температура, а — энтропия, следует выражение для дифференциала энтальпии[3][11][K 2]:
(Дифференциал энтальпии)
которое является полным дифференциалом функции [K 3]. Она представляет собой термодинамический потенциал относительно естественных независимых переменных — энтропии, давления и, возможно, числа частиц и других переменных состояния .
Понятие энтальпии существенно дополняет математический аппарат термодинамики и гидродинамики. Важно, что в изобарном процессе при постоянном изменение энтальпии
равное сумме изменения внутренней энергии и совершённой системой работы , в силу первого начала термодинамики равно количеству теплоты , сообщенной системе. Это свойство энтальпии позволяет использовать её для вычисления тепловыделения при различных изобарных процессах, например, химических.
Отношение малого количества теплоты, переданного системе в изобарном процессе, к изменению температуры является теплоёмкостью при постоянном давлении[K 4][20]:
Это экспериментально измеримая величина, и из её измерений находят температурную зависимость энтальпии.
Энтальпия — экстенсивная величина: для составной системы она равна сумме энтальпий её независимых частей. Как и внутренняя энергия, энтальпия определяется с точностью до произвольного постоянного слагаемого.
Физическое толкование[править | править код]
Рассмотрим умозрительный опыт по созданию системы, состоящей из атомов гелия в изолированной колбе с вакуумом.
Первоначально нам дано:
- Энергия системы ,
- Объём системы ; т.к. первоначально атомы газа лишены энергии, они неподвижно лежат на дне сосуда и не занимают никакого объёма.
- Давление в колбе ; в колбе вакуум.
- Объём закрытой колбы ;
Представим, что мы хотим создать из этих атомов газ. Очевидно, что для этого в систему надо подать какое-то количество энергии, но пусть также наш «энергетический бюджет» ограничен:
- Бюджет на нагрев системы и не более;
По мере подачи тепла в систему, атомы гелия будут «нагреваться», начнут двигаться. Если первоначально в колбе был вакуум , то при расширении гелию ничто не мешает занимать объём , т.е. газ не будет совершать механическую работу во время расширения. Это значит, что всё поданное тепло будет направлено на изменение внутренней энергии газа до уровня , а в случае идеального газа зависит исключительно от температуры , поэтому всё поданное будет направлено на повышение газа до температуры .
Рассмотрим тот же опыт, но с одной лишь разницей, что мы снимем с колбы механическую изоляцию, т.е. сделаем её открытой воздействию давления внешней среды. Другими словами, в отличие от первого опыта, где давление в колбе было , мы будем «создавать систему» в условиях постоянного атмосферного давления равного . Проведя тот же процесс нагрева, что и в опыте с закрытой колбой, и потратив весь доступный энергетический бюджет мы обнаружим, что мы не смогли нагреть газ до прошлого уровня , а достигли гораздо более низкой температуры , т.е. . Объясняется это тем, что часть поданной на нагрев системы была потрачено на механическую работу против сил внешней среды. Ведь до нагрева гелий не занимал никакого объёма, а по мере нагрева начал расширятся против атмосферного давления, что привело к тому, что газ совершил , которая была израсходована из внутренней энергии газа.
Собственно энтальпия и является умозрительным прибором (линейкой) измерения поданного в систему тепла для приведения её в состояние (,,). Это утверждение становится более ясным, если попробовать решить «обратную» к выше предложенной задачу: Пусть нам дан газ гелий с температурой в открытой колбе с давлением внешней среды . Вопрос: «Как измерить то количество тепла, которое было подано на эту систему для её создания?» Ответ будет в использовании , потому что согласно определению состоит из простых в измерении величин:
- для случая идеального газа , а легко измерить термометром.
- так же легко измеряется обычными приборами.
- тоже легко измеряется, если в колбе есть крышка, которая может легко перемещаться при изменении объёма газа.
В данном примере выступает как простая мера, иначе сложно измеримого, поданного в систему или забранного из системы тепла .


История вопроса[править | править код]
Понятие энтальпии было введено и развито Дж. В. Гиббсом[22][23][24] в 1875 году в классической работе «О равновесии гетерогенных веществ». Для обозначения этого понятия Гиббс использовал термин «тепловая функция при постоянном давлении»[25][26].
Автором термина «энтальпия» в его современном значении считают Х. Камерлинг-Оннеса. Впервые о его авторстве упоминает работа 1909 года[27][28] в связи с обсуждением сохранения энтальпии в эффекте Джоуля — Томсона, хотя в печатных публикациях самого Камерлинг-Оннеса это слово не встречается[29]. Что же касается буквенного обозначения , до 1920-х годов оно использовалось для количества теплоты вообще. Определение физической величины строго как энтальпии или «теплосодержания при постоянном давлении» было официально предложено Альфредом У. Портером в 1922 году[23].
Энтальпия как термодинамический потенциал[править | править код]
Поскольку внутренняя энергия является термодинамическим потенциалом относительно энтропии и объёма[30], определение энтальпии можно рассматривать как преобразование Лежандра для перехода от потенциала относительно переменных к таковому относительно переменных Как и для любого термодинамического потенциала, естественные независимые переменные совокупно с производными энтальпии по этим переменным позволяют выразить любой термодинамический параметр системы, поэтому задание термодинамического потенциала является самым общим способом задания уравнения состояния[31].
Из выражения для дифференциала энтальпии получаются ещё два уравнения состояния, непосредственно выражающие температуру и объём через энтальпию и давление[32]:
Если известна энтальпия, другие термодинамические потенциалы — внутренняя энергия , свободная энергия Гельмгольца и энергия Гиббса — могут быть получены с помощью преобразования Лежандра:
Из равных друг другу смешанных производных энтальпии выводятся две термодинамические производные, связанные третьим соотношением Максвелла[33]:
Через вторые производные энтальпии выражаются ещё две термодинамические производные:
Первая из этих производных характеризует теплоёмкость при постоянном давлении вторая — адиабатическую сжимаемость. Метод якобианов позволяет получить тождества, аналогичные соотношениям Бриджмена, для выражения любых термодинамических производных через приведённые производные энтальпии.
Зависимость энтальпии от числа частиц[править | править код]
Для состоящей из одинаковых частиц открытой системы число частиц может быть переменным[K 5]. В этом случае выражения для дифференциалов внутренней энергии и энтальпии обобщаются следующим образом[35][36]:
где — химический потенциал, который равен энергии Гиббса [37], приходящейся на одну частицу[38]: . Если частицы не рождаются и не уничтожаются в рассматриваемом процессе, можно характеризовать их количество, например, (переменной) массой тела и химический потенциал также относить к единице массы. В этом случае вклад от изменения массы вещества в дифференциалы энергии и энтальпии описывается членом , где модифицированный химический потенциал равен удельной (отнесенной к единице массы) энергии Гиббса: .

В англоязычной литературе, особенно технической, понятие открытой системы обычно отождествляют с понятием «контрольного объёма» (англ. control volume)[39], который ограничен воображаемой неподвижной контрольной[40] поверхностью, проницаемой для вещества, но оставляющей неизменной заключённый в ней объём. В то же время закрытую систему называют «контрольной массой» (англ. control mass). Последнее название подчеркивает постоянство массы (), вследствие которого справедливо приведённое выше соотношение для дифференциала внутренней энергии и термодинамическое состояние системы характеризуется только двумя параметрами, например, и . С другой стороны, при постоянстве контрольного объёма () заключённая в нём внутренняя энергия тоже характеризуется только двумя параметрами, например, энтропией и переменной массой , причём в практически важное выражение для дифференциала внутренней энергии контрольного объёма входит (удельная) энтальпия[41]:
Энергия контрольного объёма)
Если в системе присутствуют несколько различных веществ характеризующихся массами и химическими потенциалами , выражение для дифференциала энтальпии обобщается следующим образом[42][43]:
Удельная энтальпия[править | править код]
| Удельная энтальпия | |
|---|---|
| Размерность | |
| Единицы измерения | |
| СИ | Дж/кг |
| СГС | эрг/г |
| Примечания | |
| Внесистемные единицы: кал/г, кал/кг | |
| Молярная (мольная) энтальпия | |
|---|---|
| Размерность | |
| Единицы измерения | |
| СИ | Дж/моль (кг/моль) |
| СГС | эрг/моль (1 г/моль) |
| Примечания | |
| Внесистемная единица: кал/моль | |
| Плотность энтальпии | |
|---|---|
| Размерность | |
| Единицы измерения | |
| СИ | Дж/м3 |
| СГС | эрг/см3 |
Вместо экстенсивной величины энтальпии часто используют её отношение её величины к массе тела , называемое удельной энтальпией. Продолжая обозначать экстенсивные величины заглавными буквами, соответствующие им удельные величины будем обозначать строчными, за исключением удельного объёма, вместо которого введём обратную к этой величине плотность имеем:
Соотношение для полного дифференциала удельной энтальпии можно получить, разделив уравнение для дифференциала энтальпии на :
- (Дифференциал удельной энтальпии)
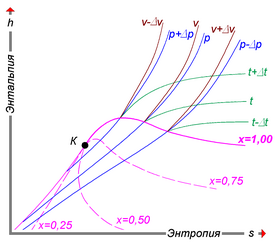
Удельную энтальпию можно представлять графически в виде -диаграммы Молье. На диаграмме кривые (изобары) для различных значений давления задают функцию [44]. Большой практический интерес представляет диаграмма Молье для воды/водяного пара[45], схематически изображённая на рисунке: синие линии — изобары, зелёные — изотермы. Область ниже красной кривой соответствует двухфазной среде пара и воды. В этой области красные линии соответствуют различным значениям величины — массовой доли водяного пара — и пересекаются в критической точке K, а изобары совпадают с изотермами и являются прямыми линиями.
Вводят также молярную (мольную) энтальпию отнесённую не к массе, а к количеству вещества в теле в молях что удобно для приложений к химии. Молярные величины обозначают нижним индексом Альтернативное определение через удельную энтальпию: где — относительная молекулярная масса, а {{{1}}} — коэффициент для перевода относительной молекулярной массы в молярную[46].
Плотности внутренней энергии и энтальпии (на единицу объёма) вводят как отношение этих величин к объёму. Отдельные обозначения для этих величин здесь не вводятся, их можно выразить через удельные величины и массовую плотность:
Деление уравнения для дифференциала энергии контрольного объёма на величину контрольного объёма даёт соотношение[47]:
- ( — дифференциал плотности энергии.)
Плотность энергии и энтальпии идеального газа[править | править код]
Для идеального газа с постоянной теплоёмкостью плотность внутренней энергии и энтальпии простым образом выражается через давление[48]:
- где — показатель адиабаты, равный для одноатомного газа, для фотонного газа (излучения чёрного тела)[49].
Энтальпия сложных термодинамических систем[править | править код]
Для термодинамических систем сложного типа, в которых термодинамическая работа[50] не сводится к работе внешних сил давления , первое начало термодинамики, а значит и выражение для дифференциала внутренней энергии, включают вклад от термодинамической работы в виде[35][51]:
где — -я обобщённая сила и — сопряжённая с ней -я обобщённая координата, во втором равенстве из общего перечня переменных выделена обобщённая сила и обобщённая координата . Для этого случая определение обобщённой энтальпии [52] даёт[53]:
Обобщенная энтальпии сохраняет смысл эквивалента теплоты для изобарного процесса[54][55], если не только давление, но и все остальные обобщённые силы поддерживаются постоянными: .
Энтальпия образования[править | править код]
Для приложений к химии в общем случае открытых систем для полного дифференциала энтальпии получаем:
Выражение для заимствуем из дифференциальной версии фундаментального уравнения Гиббса для внутренней энергии открытой термодинамической системы[56][57]:
где — масса -го независимого компонента[K 6], — химический потенциал этого компонента. Запишем уравнение Гиббса в следующем виде:
Подставив это выражение в соотношение (***), получаем дифференциальную версию фундаментального уравнения Гиббса для энтальпии:
Все химические реакции сопровождаются выделением (экзотермические) или поглощением (эндотермические) тепла. Одно из приложений энтальпии основано на том, что множество химических процессов в реальных или лабораторных условиях реализуются именно при постоянном (атмосферном) давлении. Поэтому мерой теплового эффекта реакции служит изменение энтальпии ΔН в ходе химической реакции, в результате которой исходные вещества исчезают и образуются продукты реакции. В случае экзотермических реакций система теряет тепло и ΔН — величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная. В частности, энтальпия образования — это количество теплоты, которое поглощается (если энтальпия образования положительна) или выделяется (если энтальпия образования отрицательна) при образовании сложного вещества из простых веществ.
Значение энтальпии образования и другие термодинамические свойства веществ приведены в справочниках[58][59].
Зависимость энтальпии от температуры[править | править код]
Во многих приложениях (но только не в качестве термодинамического потенциала!) энтальпию системы удобно представлять в виде функции от давления и температуры . Чтобы получить выражение для дифференциала энтальпии в переменных дифференциал энтропии выражается через :
Температурная производная энтропии выражается через (измеримую) теплоёмкость при постоянном давлении . Производная энтропии по давлению выражаются с помощью четвёртого соотношения Максвелла (G2) что даёт и:
Для идеального газа в силу закона Гей-Люссака так что выражение в квадратных скобках равно нулю, и энтальпия идеального газа зависит только от температуры. Если к тому же идеальный газ имеет постоянную темплоёмкость, его энтальпия линейно зависит от температуры[60]:
(Энтальпия идеального газа)
где — внутренняя энергия молекулы при нулевой температуре[K 7], — масса молекулы. Удельная энтальпии выражена через удельную теплоёмкость отнесённую к единице массы.
Для реальных систем изменение энтальпии при изменении температуры в изобарическом процессе практически удобно рассчитывать, если известна теплоёмкость при постоянном давлении (например, в виде ряда по степеням с эмпирическими коэффициентами[61][62]):
Поскольку разности энтальпий продуктов химической реакции и исходных веществ определяет тепловой эффект химической реакции, разность теплоёмкостей продуктов реакции и исходных веществ определяет зависимость теплового эффекта реакции от температуры (термохимический закон Кирхгофа).
Сохранение энтальпии в эффекте Джоуля — Томсона[править | править код]
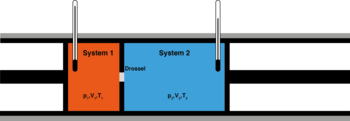
Сохранение энтальпии в процессе Джоуля — Томсона привлекается для количественного описания эффекта. Схема процесса представлена на рисунке 2. Левый поршень, вытесняя газ под давлением из объёма , совершает над ним работу . Пройдя через дроссель и расширяясь в объём , газ совершает работу над правым поршнем. Суммарная работа , совершенная над газом, равна изменению его внутренней энергии , так что энтальпия сохраняется: [63][64]
Из уравнения для дифференциала энтальпии выводится выражение для коэффициента Джоуля — Томсона , который связывает малые изменения температуры и давления в этом процессе. Приравнивание нулю дифференциала (сохраняющейся) энтальпии в переменных даёт[65][66] и
а выражение для дифференциала энтальпии в переменных даёт связь между изменениями давления и энтропии:
В процессе Джоуля — Томсона давление всегда убывает, следовательно, энтропия возрастает.
Полная энергия и полная энтальпия[править | править код]
| Полная энтальпия (удельная) (энтальпия торможения) | |
|---|---|
| Размерность | |
| Единицы измерения | |
| СИ | Дж/кг |
| СГС | эрг/г |
| Примечания | |
| Зависит от выбора системы отсчёта | |
Для движущихся тел помимо внутренней энергии, включающей кинетическую энергию теплового движения составляющих тело частиц (измеренную в системе координат, в которой тело как целое покоится), вводят также его полную энергию в системе координат, относительно которой тело движется со скоростью . Обычно полная энергия тела есть просто сумма его внутренней и кинетической энергий Более общий и строгий подход определяет не полную энергию, а её дифференциал[67]:
(Дифференциал полной энергии)
где - импульс тела и точка между векторами означает их скалярное произведение. В полную энтальпию также включается кинетическая энергия. Имеющие большое значение для физики сплошных сред удельная полная энергия и удельная полная энтальпия (обычно называемая просто «полная энтальпия» или, особенно в технических науках, «энтальпия торможения») даются формулами:
Обобщение дифференциала плотности энергии для полной энергии принимает вид[47]:
(Дифференциал плотности полной энергии)
Релятивистская энтальпия[править | править код]
| Полная энтальпия (инвариантная релятивистская) | |
|---|---|
| Размерность | |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| Лоренц-инвариант | |
| Полная энтальпия (релятивистская) | |
|---|---|
| Размерность | |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| Образует 4-вектор вместе с импульсом | |
Если скорость тела сравнима по величине со скоростью света , термодинамика строится с учётом специальной теории относительности)[67]. При этом используется инвариантная энтальпия , которая представляет собой полную энтальпию, определённую в движущейся вместе с телом системе отсчета; все величины в этой системе отсчёта обозначаем нижним индексом «0».
Релятивистская полная энергия , включает энергию покоя всех частиц тела и учитывает релятивистскую зависимость их энергии от импульса , а именно: 1) энергия и импульс образуют 4-вектор, 2) величина является Лоренц-инвариантом и 3) величина являются скоростью частицы. В неподвижной системе отсчета энтальпия и импульс движущегося тела[68][67]
образуют 4-вектор, а инвариантная энтальпии в движущейся с телом системы отсчёта даётся инвариантной функцией этого 4-вектора:
Именно полная энтальпия (а не энергия) релятивистского тела оказывается аналогом энергии релятивистской частицы. Давление лоренц-инвариантно, а преобразование объёма :
является следствием Лоренцева сокращения. Уравнение релятивистской термодинамики даётся выражением[68]:
Оно позволяет решить любой вопрос термодинамики движущихся систем, если известна функция [68]. В частности, из выражения для Дифференциала полной энергии можно получить выражение для малого количества теплоты[67]:
Энтальпия в гидродинамике[править | править код]
Энтальпия играет большую роль в гидродинамике, науке о движениях жидкостей и газов (в гидродинамике газы тоже называют жидкостями). Течения идеальной жидкости (то есть без вязкости и теплопроводности) описываются следующими уравнениями в частных производных[69]:
где — плотность; — скорость; — давление; — время; — векторный оператор частного дифференцирования по координатам ; точка между векторами в круглых скобках означает их скалярное произведение, а — ускорение силы тяжести, выраженное через гравитационный потенциал Уравнение для Дифференциала удельной энтальпии даёт: что позволяет выразить уравнение Эйлера через энтальпию:
(Уравнение Эйлера, выраженное через энтальпию)
Такое представление обладает значительными преимуществами, поскольку в силу «адабатичности» течения идеальной жидкости, задаваемого уравнением сохранения энтропии:
член в уравнении Эйлера, связанный с градиентом энтропии, во многих случаях не даёт вклада в рассчитываемые эффекты.
Поток энергии[править | править код]
Выражение для дифференциала плотности полной энергии позволяет получить скорость изменения последней[47]:
Этот раздел не завершён. |
Интеграл Бернулли[править | править код]
Из приведённых здесь термодинамических соотношений для энтальпии следует простой вывод интеграла Бернулли и в наиболее общей его форме. Закон утверждает, что вдоль линии тока для стационарного течения идеальной жидкости[70] сохраняется следующая величина:
где — гравитационный потенциал (равный для однородной силы тяжести, — ускорение свободного падения, — вертикальная координата).
1. В уравнении Эйлера для стационарного () движения идеальной жидкости в поле силы тяжести[69] ускорение силы тяжести можно выразить через гравитационный потенциал (для однородного поля ).
2. Скалярное произведение этого уравнения на единичный вектор касательный к линии тока даёт:
так как произведение градиента на единичный вектор даёт производную по направлению
3. Выражение для Дифференциала удельной энтальпии даёт:
так что
В стационарном течении идеальной жидкости все частицы, движущиеся вдоль данной линии тока, имеют одинаковую энтропию[71] (), поэтому вдоль линии тока:
См. также[править | править код]
Комментарии[править | править код]
- ↑ В России определение энтальпии как суммы закреплено действующими стандартами[7][8].
- ↑ Это соотношение носит название дифференциальной формы фундаментального уравнения Гиббса для энтальпии закрытой термодеформационной системы[12][13][14].
- ↑ Энтальпию, заданную в виде функции её естественных независимых переменных, называют интегральной формой фундаментального уравнения Гиббса[15][16][17] для энтальпии закрытой термодеформационной системы[12][18][19].
- ↑ В термодинамике при написании частных производных внизу справа указывают переменные, который при вычислении производной считают постоянным. Причина в том, что в термодинамике для одной и той же функции используют различные наборы независимых переменных, которые, во избежание неопределённости, приходится перечислять.
- ↑ Число частиц в закрытой системе тоже может быть переменным, например числе фотонов равновесного излучения в полости с абсолютно чёрными стенками[34].
- ↑ Использование масс независимых компонентов, а не масс составляющих систему веществ, позволяет учитывать химические превращения в системе без явного рассмотрения протекающих в ней химических реакций (см. статью Химическая термодинамика).
- ↑ Энергия включает в себя энергию химической связи и вносит значительный вклад в энтальпию образования газообразных сложных веществ
Примечания[править | править код]
- ↑ 1 2 3 Энтальпия // Большая российская энциклопедия. Том 35. Москва, 2017, стр. 396. Дата обращения: 1 мая 2023. Архивировано 25 марта 2023 года.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §14. Тепловая функция.
- ↑ 1 2 3 Зубарев Д. Н., Энтальпия, 1992.
- ↑ Горшков В. И., Кузнецов И. А., Основы физической химии, 2009, с. 111.
- ↑ Enthalpy, H // IUPAC Gold Book. Дата обращения: 30 ноября 2018. Архивировано 26 ноября 2018 года.
- ↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 13.
- ↑ §113-04-21. Энтальпия (Н)//ГОСТ IEC 60050-113-2015 (2015). Дата обращения: 1 декабря 2018. Архивировано из оригинала 6 февраля 2019 года.
- ↑ §54. Энтальпия(теплосодержание)//ГОСТ Р 57700.4-2017 (2017). Дата обращения: 1 декабря 2018. Архивировано из оригинала 6 февраля 2019 года.
- ↑ Зубарев Д. Н., Термодинамика, 1992.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (12.3).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (16.3).
- ↑ 1 2 Белов Г. В., Термодинамика, ч. 1, 2017, с. 155.
- ↑ Степановских Е. И. и др., Химическая термодинамика в вопросах и ответах, 2014, с. 37.
- ↑ Мечковский Л. А., Блохин А. В., Химическая термодинамика, ч. 1, 2012, с. 124.
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 312.
- ↑ Воронин Г. Ф., Основы термодинамики, 1987, с. 76.
- ↑ Мюнстер А., Химическая термодинамика, 2002, с. 90—91.
- ↑ Белов Г. В., Термодинамика, ч. 2, 2016, с. 23.
- ↑ Зарубин Д. П., Физическая химия, 2017, с. 45.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, с. 67.
- ↑ Dalton, 1909.
- ↑ Гиббс Дж. В., Термодинамические работы, 1950, Примечание 3, с. 448.
- ↑ 1 2 Howard, 2002, с. 697.
- ↑ Ахметов Б. В. и др. Физическая и коллоидная химия, 1986, с. 64.
- ↑ Гиббс Дж. В., Термодинамика. Статистическая механика, 1982, с. 96, 510.
- ↑ Henderson, Douglas; Eyring, Henry; Jost, Wilhelm. Physical Chemistry: An Advanced Treatise (неопр.). — Academic Press, 1967. — С. 29.
- ↑ Dalton, 1909, с. 863.
- ↑ Laidler; Keith. The World of Physical Chemistry (англ.). — Oxford University Press, 1995. — P. 110.
- ↑ Van Ness, 2003, с. 486.
- ↑ Зубарев Д. Н., Потенциал термодинамический, 1994, с. 89.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, §45. Термодинамические функции.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (14.4).
- ↑ Беляев Н. М., Термодинамика, 1987, с. 126.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §63. Чёрное излучение.
- ↑ 1 2 Зубарев Д. Н., Термодинамика, 1992.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнения (24.5–7).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (15.7).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (24.11).
- ↑ Automotive Encyclopedia, 2015, §1.1.2.2. Open dynamic system, с. 27.
- ↑ Белов Г. В., Термодинамика, ч. 1, 2017, с. 11.
- ↑ Automotive Encyclopedia, 2015, Уравнение (15), с. 28.
- ↑ Мюнстер А., Химическая термодинамика, 2002, с. 103.
- ↑ Кубо Р., Термодинамика, 1970, с. 24—25.
- ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 446.
- ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 449–451.
- ↑ Quantities, Units and Symbols in Physical Chemistry (англ.) 11. IUPAC (2015). Дата обращения: 7 декабря 2018. Архивировано из оригинала 11 февраля 2014 года.
- ↑ 1 2 3 Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2015, §6. Поток энергии.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнения (42.5), (43.2) и (43.4).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §63.
- ↑ Зубарев Д. Н., Работа в термодинамике, 1994.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, §12.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (45.21).
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (45.25).
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 121.
- ↑ Базаров И. П., Термодинамика, 2010, с. 113.
- ↑ Артемов А. В., Физическая химия, 2013, с. 23.
- ↑ Ипполитов Е. Г. и др., Физическая химия, 2005, с. 35.
- ↑ Search for Species Data by Chemical Formula (англ.). Дата обращения: 3 декабря 2018. Архивировано 15 июня 2017 года.
- ↑ Термодинамические свойства. Дата обращения: 3 декабря 2018. Архивировано 7 октября 2018 года.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (43.4).
- ↑ Пригожин И., Дефэй Р., Химическая термодинамика, 2009, с. 51.
- ↑ Алабовский А. Н., Недужий И. А., Техническая термодинамика и теплопередача, 1990, с. 25—26.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (19.3).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (18.1).
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (46.1).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (18.2).
- ↑ 1 2 3 4 Зубарев Д. Н., Релятивистская термодинамика, 1994.
- ↑ 1 2 3 Каллен Г., Горвиц Дж., Релятивистская термодинамика, 1972.
- ↑ 1 2 Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2015, Уравнение (2.4).
- ↑ Вишневецкий С. Л., Бернулли уравнение, 1988, с. 187.
- ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VII. §2. Функция давления.
Литература[править | править код]
- Алабовский А. Н., Недужий И. А. Техническая термодинамика и теплопередача. — 3-е изд., пераб. и доп. — Киев: Выща школа, 1990. — 256 с. — ISBN 5-11-001997-5.
- Ансельм А. И. Основы статистической физики и термодинамики. — 2-е изд., стереотип. — СПб.: Лань, 2007. — 427 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0756-9.
- Артемов А. В. Физическая химия. — М.: Академия, 2013. — 288 с. — (Бакалавриат). — ISBN 978-5-7695-9550-9.
- Ахметов Б. В., Новиченко Ю. П., Чапурин В. И. Физическая и коллоидная химия. — Л.: Химия, 1986. — 320 с.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белов Г. В. Термодинамика. Часть 1. — 2-е изд., испр. и доп. — М.: Юрайт, 2017. — 265 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-02731-0.
- Белов Г. В. Термодинамика. Часть 2. — М.: Юрайт, 2016. — 249 с. — (Бакалавриат). — ISBN 978-5-9916-7252-8.
- Беляев Н. М. Термодинамика. — Киев: Вища школа, 1987. — 344 с.
- Болгарский А. В., Мухачев Г. А., Щукин В. К. Термодинамика и теплопередача. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1975. — 496 с.
- Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-104227-4.
- Буданов В. В., Максимов А. И. Химическая термодинамика / Под ред. О. И. Койфмана. — 3-е изд., стер. — СПб.: Лань, 2017. — 320 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-2271-5.
- Вишневецкий С. Л. Бернулли уравнение // Физическая энциклопедия. — Большая Российская энциклопедия, 1988. — Т. 5: Стробоскопические приборы — Яркость. — С. 187.
- Воронин Г. Ф. Основы термодинамики. — М.: Изд-во Моск. ун-та, 1987. — 192 с.
- Гамбург Ю. Д. Химическая термодинамика. — М.: Лаборатория знаний, 2016. — 237 с. — (Учебник для высшей школы). — ISBN 978-5-906828-74-3.
- Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд., испр. — М.: Химия, 1970. — Т. 1. — 592 с.
- Гиббс Дж. В. Термодинамические работы / Пер. с англ. под ред. проф. В. К. Семенченко. — М. — Л.: Гостехиздат, 1950. — 492 с. — (Классики естествознания).
- Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).
- Горшков В. И., Кузнецов И. А. Основы физической химии. — 3-е изд. — М.: Бином. Лаборатория знаний, 2009. — 408 с. — ISBN 978-5-94774-375-3.
- Еремин В. В., Каргов С. И., Успенская И. А. и др. Основы физической химии. Теория и задачи. — М.: Экзамен, 2005. — 481 с. — (Классический университетский учебник). — ISBN 5-472-00834-4.
- Зарубин Д. П. Физическая химия. — М.: Инфра-М, 2017. — 474 с.
- Зубарев, Д. Н. Потенциал термодинамический // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 89—91. — 704 с. — ISBN 5-85270-087-8.
- Зубарев, Д. Н. Работа в термодинамике // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 193. — 704 с. — ISBN 5-85270-087-8.
- Зубарев, Д. Н. Релятивистская термодинамика // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 333—334. — 704 с. — ISBN 5-85270-087-8.
- Зубарев Д. Н. Термодинамика // Физическая энциклопедия / Ред.А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 83—87.
- Зубарев Д. Н. Энтальпия // Физическая энциклопедия / Ред. А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 616.
- Ипполитов Е. Г., Артемов А. В., Батраков В.В. Физическая химия / Под ред. Е. Г. Ипполитова. — М.: Академия, 2005. — 448 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-1456-6.
- Каллен Г., Горвиц Дж. Релятивистская термодинамика // Успехи Физических Наук : журнал. — 1972. — Т. 107, вып. 7. — С. 489—502. — doi:10.3367/UFNr.0107.197207g.0489.
- Колесников И. М., Винокуров В. А. Термодинамика физико-химических процессов. — 2-е, перераб. и доп. — М.: Нефть и газ, 2005. — 480 с. — ISBN 5-7246-0351-9.
- Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
- Ландау Л. Д., Лифшиц Е. М. Гидродинамика. — Издание 6-е, исправленное. — М.: Физматлит, 2015. — 728 с. — («Теоретическая физика», том VI). — ISBN 978-5-9221-1625-1.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М.: Физматлит, 2002. — 616 с. — («Теоретическая физика», том V). — ISBN 5-9221-0054-8.
- Мечковский Л. А., Блохин А. В. Химическая термодинамика. В двух частях. Часть 1. Феноменологическая термодинамика. Основные понятия, фазовые равновесия. — Минск: Издательство БГУ, 2012. — 141 с. — ISBN 978-985-518-635-0.
- Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — 2-е изд., стереотип. — М.: УРСС, 2002. — 296 с. — ISBN 5-354-00217-6.
- Новиков И. И. Термодинамика. — 2-е изд., испр. — СПб.: Лань, 2009. — 592 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0987-7.
- Поль Р. В. Механика, акустика и учение о теплоте. — Рипол Классик, 2013. — 490 с. — ISBN 5458431251, 9785458431255.
- Пригожин И., Дефэй Р. Химическая термодинамика / Пер. с англ. под ред. В. А. Михайлова. — 2-е изд.. — М.: Бином. Лаборатория знаний, 2009. — 533 с. — (Классика и современность. Естествознание). — ISBN 978-5-9963-0201-7.
- Савельев И. В. Курс общей физики. — М.: КноРус, 2012. — Т. 1. Механика. Молекулярная физика и термодинамика. — 528 с. — ISBN 9785406025888.
- Свиридов В. В., Свиридов А. В. Физическая химия. — СПб.: Лань, 2016. — 597 с. — ISBN 978-5-8114-2262-3.
- Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — 568 с.
- Сивухин Д. В. Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2005. — Т. II. Термодинамика и молекулярная физика. — 544 с. — ISBN 5-9221-0601-5.
- Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: Уральский издательско-полиграфический центр, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
- Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
- Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
- Хаазе Р. Термодинамика необратимых процессов / Пер. с нем. под ред. А. В. Лыкова. — М.: Мир, 1967. — 544 с.
- Хачкурузов Г. А. Основы общей и химической термодинамики. — М.: Высшая школа, 1979. — 268 с.
- Dalton J. P. Researches on the Joule-Kelvin effect, especially at low temperatures. I. Calculations for hydrogen // KNAW Proceedings. — 1909. — Т. 11. — С. 863—873.
- Howard Irmgard K. H Is for Enthalpy, Thanks to Heike Kamerlingh Onnes and Alfred W. Porter (англ.) // Journal of Chemical Education : журнал. — 2002. — Vol. 79, iss. 6. — P. 697—698. — ISSN 0021-9584. — doi:10.1021/ed079p697.
- Van Ness Hendrick C. H Is for Enthalpy (англ.) // Journal of Chemical Education : журнал. — 2003. — Vol. 80, iss. 5. — P. 486. — ISSN 0021-9584. — doi:10.1021/ed080p486.1.
- Part 1 : Engines — Fundamentals // Encyclopedia of Automitive Engineering / Editors-in-Chief : David Crolla, David E. Foster, Toshio Kobayashi, Nicolas Vaughan. — John Wiley & Sons, 2015. — Т. 1. — 607 с. — ISBN 978-0-470-97402-5.


















































































































![{\displaystyle \quad \mathrm {d} H=C_{P}\mathrm {d} T+\left[V-T\left({\frac {\partial V}{\partial T}}\right)_{P}\right]\mathrm {d} P.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db8b72626dbc316bfcff5dcbb2aae49c93912304)




















![{\displaystyle C_{P}\mathrm {d} T+\left[V-T\left({\frac {\partial V}{\partial T}}\right)_{P}\right]\mathrm {d} P=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10e30be2110fa951c716fb887b72bb50a0fe82b4)




























































