Кривизна

В дифференциальной геометрии, кривизна́ — собирательное название ряда количественных характеристик (скалярных, векторных, тензорных), описывающих отклонение того или иного геометрического «объекта» (кривой, поверхности, риманова пространства и т. д.) от соответствующих «плоских» объектов (прямая, плоскость, евклидово пространство и т. д.).

Обычно кривизна определяется для каждой точки на «объекте» и выражается как значение некоторого дифференциального выражения 2-го порядка. Иногда кривизна определяется в интегральном смысле, например, как мера, такие определения используют для «объектов» пониженной гладкости. Как правило, тождественное обращение в нуль кривизны во всех точках влечёт локальное совпадение изучаемого «объекта» с «плоским» объектом.

В этой статье приводятся только несколько простейших примеров определений понятия кривизны.

Кривизна кривой

Пусть $\gamma (t)$ — регулярная кривая в $d$-мерном евклидовом пространстве, параметризованная длиной. Тогда

$\kappa =|{\ddot {\gamma }}(t)|$

называется кривизной кривой $\gamma$ в точке $p=\gamma (t)$, здесь ${\ddot {\gamma }}(t)$ обозначает вторую производную по $t$. Вектор

$k={\ddot {\gamma }}(t)$

называется вектором кривизны $\gamma$ в точке $p=\gamma (t)$.

Очевидно, это определение можно переписать через вектор касательной $\tau (t)={\dot {\gamma }}(t)$:

$k={\dot {\tau }}(t),$

где одна точка над буквой означает первую производную по t.

float

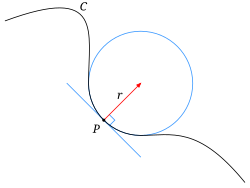
Для кривой, заданной параметрически в общем случае (параметр не обязательно является длиной), кривизна отображается формулой

$\kappa ={\frac {|{\dot {\gamma }}\times {\ddot {\gamma }}|}{|{\dot {\gamma }}|^{3}}}$,

где ${\dot {\gamma }}$ и ${\ddot {\gamma }}$ соответственно обозначают первую и вторую производную радиус-вектора $\gamma$ в требуемой точке (при этом под крестом $\times$ для кривой в трехмерном пространстве можно понимать векторное произведение, для кривой в двумерном пространстве — псевдоскалярное произведение, а для кривой в пространстве произвольной размерности — внешнее произведение).

Для кривой на декартовой плоскости, заданной уравнением $y=y(x)$, кривизна вычисляется по формуле:

$\kappa (x)={\frac {|y''|}{({\sqrt {1+y'^{2}}})^{3}}}$

Для того чтобы кривая $\gamma$ совпадала с некоторым отрезком прямой или со всей прямой, необходимо и достаточно, чтобы кривизна (или вектор кривизны) тождественно равнялась нулю.

Величина, обратная кривизне кривой ($r=1/\kappa$), называется радиусом кривизны; он совпадает с радиусом соприкасающейся окружности в данной точке кривой. Центр этой окружности называется центром кривизны. Если кривизна кривой равна нулю, то соприкасающаяся окружность вырождается в прямую.

Кривизна поверхности

Пусть $\Phi$ есть регулярная поверхность в трёхмерном евклидовом пространстве. Пусть $p$ — точка $\Phi$, $T_{p}$ — касательная плоскость к $\Phi$ в точке $p$, $n$ — единичная нормаль к $\Phi$ в точке $p$, а — $\pi _{e}$ плоскость, проходящая через $n$ и некоторый единичный вектор $e$ в $T_{p}$. Кривая $\gamma _{e}$, получающаяся как пересечение плоскости $\pi _{e}$ с поверхностью $\Phi$, называется нормальным сечением поверхности $\Phi$ в точке $p$ в направлении $e$. Величина

$\kappa _{e}=k\cdot n$

где $\cdot$ обозначает скалярное произведение, а $k$ — вектор кривизны $\gamma _{e}$ в точке $p$, называется нормальной кривизной поверхности $\Phi$ в направлении $e$. С точностью до знака нормальная кривизна равна кривизне кривой $\gamma _{e}$.

В касательной плоскости $T_{p}$ существуют два перпендикулярных направления $e_{1}$ и $e_{2}$ такие, что нормальную кривизну в произвольном направлении можно представить с помощью так называемой формулы Эйлера:

$\kappa _{e}=\kappa _{1}\cos ^{2}\alpha +\kappa _{2}\sin ^{2}\alpha$

где $\alpha$ — угол между $e_{1}$ и $e$, a величины $\kappa _{1}$ и $\kappa _{2}$ нормальные кривизны в направлениях $e_{1}$ и $e_{2}$, они называются главными кривизнами, а направления $e_{1}$ и $e_{2}$ — главными направлениями поверхности в точке $p$. Главные кривизны являются экстремальными значениями нормальных кривизн. Структуру нормальных кривизн в данной точке поверхности удобно графически изображать с помощью индикатрисы Дюпена.

Величина

$H=\kappa _{1}+\kappa _{2}$, (иногда ${\frac {\kappa _{1}+\kappa _{2}}{2}}$)

называется средней кривизной поверхности. Величина

$K=\kappa _{1}\kappa _{2}$

называется гауссовой кривизной поверхности.

Гауссова кривизна является объектом внутренней геометрии поверхностей, в частности не изменяется при изометрических изгибаниях.

См. также

• Аффинная кривизна
• Дифференциальная геометрия кривых
• Дифференциальная геометрия поверхностей
• Поверхность
• Тензор кривизны
• Форма кривизны

Литература

• Погорелов А. В. Дифференциальная геометрия (6-е издание). М.: Наука, 1974.
• Рашевский П. К. Курс дифференциальной геометрии (3-е издание). М.-Л.: ГИТТЛ, 1950.