Алгоритм кластеризации OPTICS
Упорядочение точек для обнаружения кластерной структуры (англ. Ordering points to identify the clustering structure, OPTICS) — это алгоритм нахождения[1] кластеров в пространственных данных на основе плотности. Алгоритм презентовали Михаэл Анкерст, Маркус М. Бройниг, Ганс-Петер Кригель и Ёрг Сандер[2]. Основная идея алгоритма похожа на DBSCAN[3], но алгоритм предназначен для избавления от одной из главных слабостей алгоритма DBSCAN — проблемы обнаружения содержательных кластеров в данных, имеющих различные плотности. Чтобы это сделать, точки базы данных (линейно) упорядочиваются так, что пространственно близкие точки становятся соседними в упорядочении. Кроме того, для каждой точки запоминается специальное расстояние, представляющее плотность, которую следует принять для кластера, чтобы точки принадлежали одному кластеру. Это представлено в виде дендрограммы.
Основная идея[править | править код]
Подобно DBSCAN, алгоритм OPTICS требует два параметра — параметр ε описывает максимальное расстояние (радиус), принимаемое во внимание, а параметр MinPts описывает число точек, требующихся для образования кластера. Точка p является основной точкой, если по меньшей мере MinPts точек находятся в её ε-окрестности . В отличие от DBSCAN, алгоритм OPTICS рассматривает также точки, которые являются частью более плотного кластера, так что каждой точке назначается основное расстояние, которое описывает расстояние до MinPts-ой ближайшей точки:
Здесь core-dist = основное расстояние, = -ое в порядке возрастания расстояние до .
Достижимое расстояние точки o от точки p равно либо расстоянию между o и p, либо основному расстоянию точки p, в зависимости от того, какая величина больше:
Здесь reachability-dist = достижимое расстояние.
Если p и o являются ближайшими соседями, и , можно предположить, что p и o принадлежат тому же кластеру.
Как основное, так и достижимое расстояния не определены, если нет достаточно плотного кластера (применительно к ε). Если взять достаточно большое ε, этого никогда не произойдёт, но тогда любой запрос ε-соседства возвращает всю базу данных, что приводит ко времени работы . Параметр ε требуется для отсечения неплотных кластеров, которые более неинтересны, и тем самым ускорить алгоритм.
Параметр ε, строго говоря, не обязателен. Он может просто быть установлен в максимальное возможное значение. Однако при доступности пространственного индекса он влияет на сложность вычислений. OPTICS отличается от DBSCAN тем, что этот параметр не учитывается, если ε и может влиять, то только тем, что задаёт максимальное значение.
Псевдокод[править | править код]
Основной подход алгоритма OPTICS такой же, как у DBSCAN, но вместо поддержки множества известных, но ещё необработанных членов кластера, используется очередь с приоритетом (то есть индексированная куча).
OPTICS(DB, eps, MinPts)
для каждой точки p из DB
p.достижимое_расстояние=не_определено
для каждой необработанной точки p из DB
N=получитьСоседей (p, eps)
пометить p как обработанную
поместить p в упорядоченный список
если (основное_расстояние (p, eps, Minpts) != не_определено)
Seeds=пустая приоритетная очередь
обновить(N, p, Seeds, eps, Minpts)
для каждой следующей q из Seeds
N'=получитьСоседей(q, eps)
пометить q как обработанную
поместить q в упорядоченный список
если (основное_расстояние(q, eps, Minpts) != не_определено)
обновить(N', q, Seeds, eps, Minpts)
В процедуре обновить(), приоритетная очередь Seeds обновляется по -соседям точек и соответственно:
обновить (N, p, Seeds, eps, Minpts)
coredist=основное_расстояние(p, eps, MinPts)
для каждого o в N
если (o не обработана)
новое_дост_расст=max(coredist, dist(p,o))
если (o.достижимое_расстояние == не_определено) // точка o не в Seeds
o.достижимое_расстояние=новое_дост_расст
Seeds.вставить(o, новое_дост_расст)
иначе // точка o в Seeds, проверить на улучшение
если (новое_дост_раст < o.достижимое_расстояние)
o.достижимое_расстояние=новое_дост_раст
Seeds.передвинуть_вверх(o, новое_дост_раст)
OPTICS помещает точки в определённом порядке, помечая их наименьшим достижимым расстоянием (в оригинальном алгоритме основное расстояние также запоминается, но это не требуется для дальнейшей обработки).
Извлечение кластеров[править | править код]
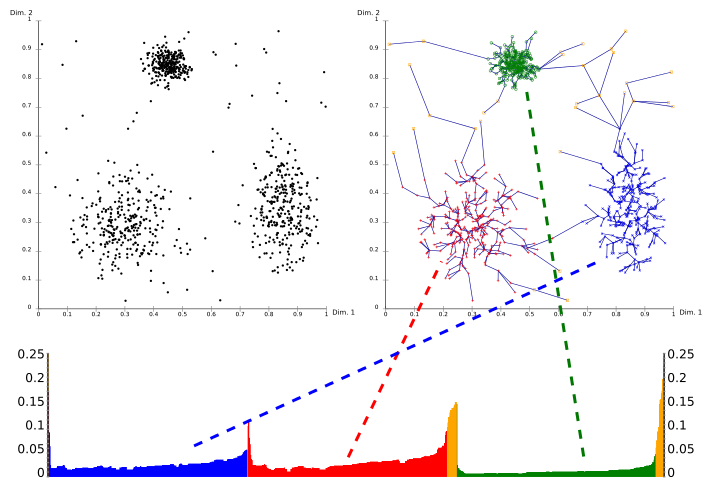
Используя график достижимости (особый вид древовидной схемы), легко получить иерархическую структуру кластеров. Это двумерный график, на котором точки по оси x откладываются в порядке их обработки алгоритмом OPTICS, а по оси y откладывается достижимое расстояние. Поскольку точки, принадлежащие кластеру, имеют небольшое достижимое расстояние до ближайшего соседа, кластеры выглядят как долины на графике достижимости. Чем глубже долина, тем плотнее кластер.
Рисунок выше иллюстрирует эту концепцию. В верхней левой области рисунка показан смоделированный набор данных. Область рисунка верху справа визуализирует остовное дерево, полученное алгоритмом OPTICS, а нижняя часть рисунка показывает график достижимости, как его получает OPTICS. Цвета на этом графике являются метками и не вычисляются алгоритмом. Однако хорошо видно, как долины на графике соответствуют кластерам приведённого набора данных. Жёлтые точки на этом изображении считаются шумом и не соответствуют никаким долинам. Они обычно не назначаются никаким кластерам, за исключением всеобъемлющего кластера «все данные» в иерархическом результате.
Извлечение кластеров из такого графика может быть осуществлено вручную путём выбора интервалов по оси x после просмотра графика, путём выбора порога по оси y (тогда результат подобен DBSCAN-кластеризации с теми же значениями параметров и minPts, в нашем случае значение 0,1 может дать хорошие результаты), или с помощью различных алгоритмов, которые пытаются определить долины по крутизне графика, по изгибу или по локальным максимумам. Кластеризации, полученные таким образом, обычно являются иерархическими и не могут быть получены одним прогоном алгоритма DBSCAN.
Сложность[править | править код]
Подобно DBSCAN алгоритм OPTICS обрабатывает каждую точку только один раз и выполняет один запрос -соседства во время этой обработки. Если задан пространственный индекс, который гарантирует работу запроса соседства за время , получим общее время работы . Авторы оригинальной статьи по OPTICS сообщают о константном замедлении в 1,6 раза по сравнению с DBSCAN. Заметим, что значение может сильно влиять на затраты алгоритма, поскольку слишком большое значение может увеличивать сложность запроса соседства до линейной.
В частности, выбор (больше, чем максимальное расстояние в наборе данных) возможен, но, очевидно, ведёт к квадратичной сложности, поскольку запрос списка соседей возвращает весь набор данных. Даже если никакой пространственный индекс не доступен, это приводит к дополнительным затратам в поддержке кучи. Таким образом, следует выбрать должным образом для набора данных.
Расширения[править | править код]
OPTICS-OF[4] является алгоритмом выявления аномалий, основанном на OPTICS. В основном он используется для выделения выбросов из существующего прогона алгоритма OPTICS с малыми затратами по сравнению с другим методом выделения выброса. Лучшая известная версия алгоритма выделения локального уровня выброса основывается на тех же концепциях.
DeLi-Clu[5], (англ. Density-Link-Clustering) комбинирует идеи из метода одиночной кластеризации и алгоритма OPTICS, исключая параметр и добавляя улучшение эффективности по сравнению с OPTICS.
HiSC[6] является иерархическим методом кластеризации подпространств (параллельно осям), основанным на OPTICS.
HiCO[7] является иерархическим алгоритмом корреляционной кластеризации, основанным на OPTICS.
DiSH[8] является улучшением алгоритма HiSC, которое может найти более сложные иерархии.
FOPTICS[9] является быстрой реализацией с помощью случайных проекций.
HDBSCAN*[10] основан на усовершенствовании алгоритма DBSCAN исключением граничных точек из кластеров и отсюда следует более строгое определение уровней плотности (по Хартигану)[11].
Доступность[править | править код]
Реализация на Java OPTICS, OPTICS-OF, DeLi-Clu, HiSC, HiCO и DiSH доступны в системе интеллектуального анализа данных ELKI (с ускоренным индексом для некоторых функций расстояния и с автоматическим выделением кластеров с помощью метода ξ). Другая реализация на языке Java включает расширение набора средств Weka (без поддержки выделения кластеров с помощью ξ). Пакет на языке R «dbscan» включает реализацию на языке C++ алгоритма OPTICS (как с традиционным выделением кластеров, подобным dbscan, так и ξ), используя K-мерное дерево для ускорения индекса для евклидова расстояния.
Для языка Python имеются следующие реализации. OPTICS доступен в библиотеке PyClustering. HDBSCAN доступен в библиотеке hdbscan, которая построена на основе scikit learn.
Примечания[править | править код]
- ↑ Kriegel, Kröger, Sander, Zimek, 2011, с. 231–240.
- ↑ Ankerst, Breunig, Kriegel, Sander, 1999, с. 49–60.
- ↑ Ester, Kriegel, Sander, Xu, 1996, с. 226–231.
- ↑ Breunig, Kriegel, Ng, Sander, 1999, с. 262–270.
- ↑ Achtert, Böhm, Kröger, 2006, с. 119–128.
- ↑ Achtert, Böhm, Kriegel, Kröger, Müller-Gorman, Zimek, 2006, с. 446–453.
- ↑ Achtert, Böhm, Kröger, Zimek, 2006, с. 119–128.
- ↑ Achtert, Böhm, Kriegel, Kröger, Müller-Gorman, Zimek, 2007, с. 152–163.
- ↑ Schneider, Vlachos, 2013.
- ↑ Campello, Moulavi, Zimek, Sander, 2015, с. 1–51.
- ↑ Hartigan, 1975.
Литература[править | править код]
- Hans-Peter Kriegel, Peer Kröger, Jörg Sander, Arthur Zimek. Density-based clustering // Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery. — 2011. — Май (т. 1, вып. 3). — С. 231–240. — doi:10.1002/widm.30.
- Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel, Jörg Sander. OPTICS: Ordering Points To Identify the Clustering Structure // =ACM SIGMOD international conference on Management of data. — ACM Press, 1999. — С. 49–60.
- Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu. A density-based algorithm for discovering clusters in large spatial databases with noise // Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96) / Evangelos Simoudis, Jiawei Han, Usama M. Fayyad. — AAAI Press, 1996. — С. 226–231. — ISBN 1-57735-004-9.
- Markus M. Breunig, Hans-Peter Kriegel, Raymond T. Ng, Jörg Sander. OPTICS-OF: Identifying Local Outliers // Principles of Data Mining and Knowledge Discovery. — Springer-Verlag, 1999. — С. 262–270. — ISBN 978-3-540-66490-1. — doi:10.1007/b72280.
- Achtert E., Böhm C., Kröger P. DeLi-Clu: Boosting Robustness, Completeness, Usability, and Efficiency of Hierarchical Clustering by a Closest Pair Ranking. — 2006. — Т. 3918. — С. 119–128. — (Lecture Notes in Computer Science). — ISBN 978-3-540-33206-0. — doi:10.1007/11731139_16.
- Achtert E., Böhm C., Kriegel H. P., Kröger P., Müller-Gorman I., Zimek A. Finding Hierarchies of Subspace Clusters // LNCS: Knowledge Discovery in Databases: PKDD 2006. — 2006. — Т. 4213. — С. 446–453. — ISBN 978-3-540-45374-1. — doi:10.1007/11871637_42.
- Achtert E., Böhm C., Kröger P., Zimek A. Mining Hierarchies of Correlation Clusters // Proc. 18th International Conference on Scientific and Statistical Database Management (SSDBM). — 2006. — С. 119–128. — ISBN 0-7695-2590-3. — doi:10.1109/SSDBM.2006.35.
- Achtert E., Böhm C., Kriegel H. P., Kröger P., Müller-Gorman I., Zimek A. Detection and Visualization of Subspace Cluster Hierarchies // LNCS: Advances in Databases: Concepts, Systems and Applications. — 2007. — Т. 4443. — С. 152–163. — ISBN 978-3-540-71702-7. — doi:10.1007/978-3-540-71703-4_15.
- Johannes Schneider, Michail Vlachos. Fast parameterless density-based clustering via random projections // 22nd ACM International Conference on Information and Knowledge Management(CIKM). — ACM, 2013.
- Campello R. J. G. B., Davoud Moulavi, Arthur Zimek, Jörg Sander. Hierarchical Density Estimates for Data Clustering, Visualization, and Outlier Detection // ACM Transactions on Knowledge Discovery from Data. — 2015. — Т. 10, вып. 1. — С. 1–51. — doi:10.1145/2733381.
- John A. Hartigan. Clustering algorithms. — John Wiley & Sons, 1975. — (Wiley series in probability and mathematical ststistics). — ISBN 0-471-35645-X.