Метод хорд
Метод хорд — итерационный численный метод приближённого нахождения корня уравнения.
Геометрическое описание метода секущих[править | править код]
Будем искать нуль функции . Выберем две начальные точки и и проведем через них прямую. Она пересечет ось абсцисс в точке . Теперь найдем значение функции с абсциссой . Временно будем считать корнем на отрезке . Пусть точка имеет абсциссу и лежит на графике. Теперь вместо точек и мы возьмём точку и точку . Теперь с этими двумя точками проделаем ту же операцию и так далее, то есть будем получать две точки и и повторять операцию с ними. Отрезок, соединяющий последние две точки, пересекает ось абсцисс в точке, значение абсциссы которой можно приближённо считать корнем. Эти действия нужно повторять до тех пор, пока не получим значение корня с нужным приближением.
Алгебраическое описание метода секущих[править | править код]
Пусть — абсциссы концов хорды, — уравнение функции, решаемое методом секущих. Найдём коэффициенты и из системы уравнений
Вычтем из первого уравнения второе:
затем найдём коэффициенты и :
тогда
Уравнение принимает вид
Таким образом, теперь можем найти первое приближение к корню, полученное методом секущих:
Теперь возьмём координаты и и повторим все проделанные операции, найдя новое приближение к корню. Таким образом, итерационная формула метода секущих имеет вид:
Повторять операцию следует до тех пор, пока не станет меньше или равно заданному значению погрешности.
Метод хорд с итерационной формулой[править | править код]

Иногда методом секущих называют метод с итерационной формулой
Этот метод можно считать разновидностью метода простой итерации, и он имеет меньшую скорость сходимости. Далее для определённости этот метод будем называть методом хорд, а метод, описанный в предыдущем разделе, методом секущих.
Пример использования метода секущих[править | править код]
Решим уравнение методом секущих. Зададимся точностью ε=0.001 и возьмём в качестве начальных приближений и концы отрезка, на котором отделён корень: и , числовые значения и выбраны произвольно. Вычисления ведутся до тех пор, пока не будет выполнено неравенство .
В нашем примере, в значение подставляется , а в значение подставляется . Значение это будет числовое значение полученное по этой формуле. В дальнейшем подставляем в формулу в значение , а в значение .
По этой формуле последовательно получаем (подчёркнуты верные значащие цифры):

; ; ; ; ; ; ; ; ; ;
Проверим, что метод работает и в том случае, если и выбраны по одну и ту же сторону от корня (то есть, если корень не отделён на отрезке между начальными приближениями). Возьмём для того же уравнения и . Тогда: (картинка уже не из метода секущих, а из метода дихотомии)
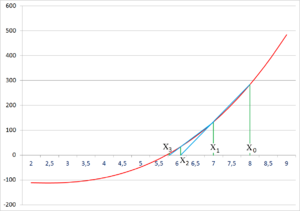
; ; ; ; ; ; ; ;
Мы получили то же значение корня за то же число итераций.
Сходимость метода секущих[править | править код]
Итерации метода секущих сходятся к корню , если начальные величины и достаточно близки к корню. Метод секущих является быстрым. Порядок сходимости α равен золотому сечению:
Таким образом, порядок сходимости больше линейного, но не квадратичен, как у родственного метода Ньютона.
Этот результат справедлив, если дважды дифференцируема и корень не является кратным — .
Как и для большинства быстрых методов, для метода секущих трудно сформулировать условия сходимости. Если начальные точки достаточно близки к корню, то метод сходится, но нет общего определения «достаточной близости». Сходимость метода определяется тем, насколько функция «волниста» в . Например, если в интервале есть точка, в которой , то процесс может не сходиться.
Критерий и скорость сходимости метода хорд[править | править код]
Если — дважды непрерывно дифференцируемая функция, и знак сохраняется на рассматриваемом промежутке, то полученные приближения будут сходиться к корню монотонно. Если корень уравнения находится на отрезке , производные и на этом промежутке непрерывны и сохраняют постоянные знаки и , то можно доказать[1], что погрешность приближенного решения стремится к нулю при , то есть метод сходится и сходится со скоростью геометрической прогрессии (при этом говорят, что он имеет линейную скорость сходимости).
Историческая справка[править | править код]
Первым, кто смог найти приближённые решения кубических уравнений, был Диофант, тем самым заложив основу метода хорд. Сохранившиеся работы Диофанта сообщают об этом. Однако первым, кто понял его методы, был Ферма в XVII веке, а первым, кто дал объяснение методу хорд, был Ньютон (1670-е гг.).[2]
Реализация[править | править код]
C++[править | править код]
#include <iostream>
#include <math.h>
double f(double x) {
return sqrt(fabs(cos(x))) - x; // Заменить функцией, корни которой мы ищем
}
// a, b - пределы хорды, epsilon — необходимая погрешность
double findRoot(double a, double b, double epsilon) {
while(fabs(b - a) > epsilon) {
a = a - (b - a) * f(a) / (f(b) - f(a));
b = b - (a - b) * f(b) / (f(a) - f(b));
}
// a, b — (i - 1)-й и i-й члены
return b;
}
Python[править | править код]
from math import sin
from typing import Callable
import unittest
def secant(f: Callable[[float], float], x0: float, eps: float=1e-7, kmax: int=1e3) -> float:
"""
solves f(x) = 0 by secant method with precision eps
:param f: f
:param x0: starting point
:param eps: precision wanted
:return: root of f(x) = 0
"""
x, x_prev, i = x0, x0 + 2 * eps, 0
while abs(x - x_prev) >= eps and i < kmax:
x, x_prev, i = x - f(x) / (f(x) - f(x_prev)) * (x - x_prev), x, i + 1
return x
class TestSecant(unittest.TestCase):
def test_0(self):
def f(x: float) -> float:
return x**2 - 20 * sin(x)
x0, x_star = 2, 2.7529466338187049383
self.assertAlmostEqual(secant(f, x0), x_star)
if __name__ == '__main__':
unittest.main()
Модификации[править | править код]
Метод ложного положения отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.
См. также[править | править код]
- Метод Ньютона (метод касательных)
- Метод простой итерации
- Обратная параболическая интерполяция
Литература[править | править код]
- Демидович Б. П. и Марон И. А. Основы вычислительной математики. — Наука, 1970. — С. 664.
- Бахвалов, Жидков, Кобельков. Численные методы. — Наука. — ISBN 5-94774-060-5.
Примечания[править | править код]
Ссылки[править | править код]
- Решение уравнений методом хорд онлайн
- «Методы решения алгебраических уравнений» на сайте www.petrsu.ru Архивная копия от 8 января 2018 на Wayback Machine
- «Методы дихотомии» на сайте www.epikoiros.narod.ru
- Ю. Губарь, Курс «Введение в математическое моделирование» Лекция 4: Численные методы решения нелинейных уравнений // Интуит.ру, 15.03.2007





![{\displaystyle [x_{1};x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d111814e88fbf11c97a4fb2610e3706fc9a2d3b0)


















































![{\displaystyle [x_{0},x_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec10faf54bec6a09b997bebef2b4417ec2ebc8b0)



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


