Расстояние Хэмминга
 |
 |
 | |
 | |
Расстоя́ние Хэ́мминга (кодовое расстояние) — число позиций, в которых соответствующие символы двух слов одинаковой длины различны[1]. В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых q-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.
Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей: в этом случае расстоянием Хэмминга между двумя двоичными последовательностями (векторами) и длины называется число позиций, в которых они различны. В такой формулировке расстояние Хэмминга вошло в словарь алгоритмов и структур данных национального института стандартов и технологий США (англ. NIST Dictionary of Algorithms and Data Structures). Расстояние Хэмминга является частным случаем метрики Минковского (при соответствующем определении вычитания):
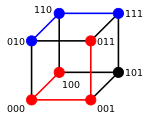
Два слова, расстояние Хэмминга между которыми равно 1, называют соседними.
В некоторых системах счисления, например, в коде Грея, целые кодированные числа, различающиеся на 1, имеют расстояние Хэмминга равное 1. Говорят, что такие числа являются «соседними».
Соседнее кодирование важно при проектировании логических устройств, где необходимо исключить логические гонки.
Примеры[править | править код]
Алгоритм[править | править код]
def hamming_distance(string1, string2):
if (len(string1) != len(string2)):
raise Exception('Strings must be of equal length.')
dist_counter = 0
for n in range(len(string1)):
if string1[n] != string2[n]:
dist_counter += 1
return dist_counter
Свойства[править | править код]
Множество слов равной длины образуют метрическое пространство, где для каждой пары элементов пространства определено число — расстояние Хэмминга удовлетворяющее аксиомам метрики:
- (аксиома тождества).
- (аксиома симметрии).
- (аксиома треугольника или неравенство треугольника).
- Из аксиом следует неотрицательность расстояния, поскольку
- .
- Если неравенство треугольника представить в виде
- для всех и ,
- тогда из аксиомы тождества и неравенства треугольника следует аксиома симметрии.
Расстояние Хэмминга всегда:
- где — длина слов в символах.
Применения[править | править код]
Расстояние Хэмминга в биоинформатике и геномике[править | править код]
Для нуклеиновых кислот (ДНК и РНК) возможность гибридизации двух полинуклеотидных цепей с образованием вторичной структуры — двойной спирали — зависит от степени комплементарности нуклеотидных последовательностей обеих цепей. При увеличении расстояния Хэмминга количество водородных связей, образованных комплементарными парами оснований уменьшается и, соответственно, уменьшается стабильность двойной цепи. Начиная с некоторого граничного расстояния Хэмминга гибридизация становится невозможной.
При эволюционном расхождении гомологичных ДНК-последовательностей расстояние Хэмминга является мерой, по которой можно судить о времени, прошедшем с момента расхождения гомологов, например, о длительности эволюционного отрезка, разделяющего гены-гомологи и ген-предшественник.
Телекоммуникации[править | править код]
Алгоритм используется в телекоммуникациях для подсчета количества неправильных бит в слове фиксированной длины для оценки ошибки и поэтому иногда называется расстоянием сигналов (англ. signal distance).
См. также[править | править код]
Примечания[править | править код]
- ↑ Hamming distance: The number of digit positions in which the corresponding digits of two binary words of the same length are different (Federal Standard 1037C Архивная копия от 2 марта 2009 на Wayback Machine).
Литература[править | править код]
- Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир, 1986. — 576 с.















