Сортировка расчёской

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
Сортировка расчёской
Визуализация сортировки расчёской
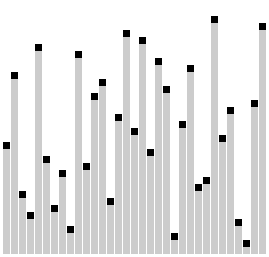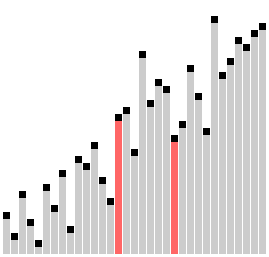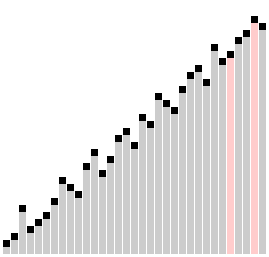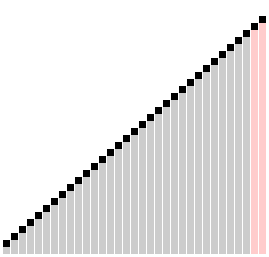Визуализация сортировки расчёской
Предназначение Алгоритм сортировки
Худшее время
Лучшее время
Среднее время
Затраты памяти
Логотип Викисклада Медиафайлы на Викискладе

Сортировка расчёской (англ. comb sort) — это довольно[уточнить] упрощённый алгоритм сортировки, изначально спроектированный Влодзимежем Добосевичем в 1980 г. Позднее он был переоткрыт и популяризован в статье Стивена Лэйси и Ричарда Бокса в журнале Byte Magazine в апреле 1991 г[1]. Сортировка расчёской улучшает сортировку пузырьком, и конкурирует с алгоритмами, подобными быстрой сортировке. Основная идея — устранить черепах, или маленькие значения в конце списка, которые крайне замедляют сортировку пузырьком (кролики, большие значения в начале списка, не представляют проблемы для сортировки пузырьком).

В сортировке пузырьком, когда сравниваются два элемента, промежуток (расстояние друг от друга) равен 1. Основная идея сортировки расчёской в том, что этот промежуток может быть гораздо больше, чем единица (сортировка Шелла также основана на этой идее, но она является модификацией сортировки вставками, а не сортировки пузырьком).

Алгоритм[править | править код]

В «пузырьке», «шейкере» и «чёт-нечете» при переборе массива сравниваются соседние элементы. Основная идея «расчёски» в том, чтобы первоначально брать достаточно большое расстояние между сравниваемыми элементами и по мере упорядочивания массива сужать это расстояние вплоть до минимального. Таким образом, мы как бы причёсываем массив, постепенно разглаживая на всё более аккуратные пряди. Первоначальный разрыв между сравниваемыми элементами лучше брать с учётом специальной величины, называемой фактором уменьшения, который может быть, например, 1.25. Сначала расстояние между элементами максимально, то есть равно размеру массива минус один. Затем, пройдя массив с этим шагом, необходимо поделить шаг на фактор уменьшения и пройти по списку вновь. Так продолжается до тех пор, пока разность индексов не достигнет единицы. В этом случае сравниваются соседние элементы как и в сортировке пузырьком, но такая итерация одна.

Реализация[править | править код]

Ассемблерная вставка для x86-64 на Си[править | править код]

Для корректной работы следующей функции сортируемый массив должен быть глобальным.

const int N = 100;
int a[N];
double factor = 1.25;
void sort()
{
    asm(
    // variables
    "movsd factor(%rip), %xmm1\n"   // factor in xmm1
    "xorl %r9d, %r9d\n"             // counter j in the inside cycle in r9d
    "movl N(%rip), %r10d\n"         // n in r10d
    "leaq a(%rip), %r12\n"          // a in r12

    // making step
    "cvtsi2sdl %r10d, %xmm0\n"
    "divsd %xmm1, %xmm0\n"
    "cvttsd2sil %xmm0, %r8d\n"      // step in r8d

    "jmp Check_step\n"

    "Increment_j:"
    "incl %r9d\n"

    "Check_j:"
    "movl %r9d, %r11d\n"
    "addl %r8d, %r11d\n"
    "cmpl %r10d, %r11d\n"
    "jge Change_step\n"

    "movl (%r12, %r9, 4), %r13d\n"  // a[j]
    "movl %r9d, %r11d\n"            // new index in r11d
    "addl %r8d, %r11d\n"            // new index = j + step
    "movl (%r12, %r11, 4), %r14d\n" // a[j + 1]
    "cmpl %r14d, %r13d\n"
    "jle Increment_j\n"

    "movl %r13d, (%r12, %r11, 4)\n"
    "movl %r14d, (%r12, %r9, 4)\n"
    "jmp Increment_j\n"

    "Change_step:"
    "cvtsi2sdl %r8d, %xmm0\n"
    "divsd %xmm1, %xmm0\n"
    "cvttsd2sil %xmm0, %r8d\n"

    "Check_step:"
    "cmpl $1, %r8d\n"
    "jl Off\n"
    "xorl %r9d, %r9d\n"
    "jmp Check_j\n"

    "Off:"
    );
}

Реализация на языке Паскаль[править | править код]

procedure CombSort(var v: array of Integer);
var
  i, gap, t: Integer;
  IsSorted: Boolean;
begin
  gap:=High(v); IsSorted:=False;
  while not IsSorted do begin
    gap:=Trunc(gap/1.25);
    if gap<=1 then begin
      gap:=1; IsSorted:=True;
    end;
    for i:=0 to High(v)-gap do
      if v[i]>v[i+gap] then begin
        t:=v[i]; v[i]:=v[i+gap]; v[i+gap]:=t;
        IsSorted:=False;
      end;
  end;
end;

var
  a: array [0..19] of Integer;
  i: Integer;
begin
  for i:=Low(a) to High(a) do a[i]:=High(a)-i;
  CombSort(a);
  for i:=Low(a) to High(a) do Write(' ',a[i]); WriteLn;
end.

Реализация на C++[править | править код]

void comb(std::vector<int> &data) // data — название вектора  (передаём по ссылке, чтобы вызов comb(array) менял вектор array)
{
	double factor = 1.25; // фактор уменьшения
	int step = data.size() - 1; // шаг сортировки
    
    //Последняя итерация цикла, когда step==1 эквивалентна одному проходу сортировки пузырьком
	while (step >= 1)
	{
		for (int i = 0; i + step < data.size(); i++)
		{
			if (data[i] > data[i + step])
			{
				std::swap(data[i], data[i + step]);
			}
		}
		step /= factor;
	}
}

Реализация на Java[править | править код]

public static <E extends Comparable<? super E>> void sort(E[] input) {
    int gap = input.length;
    boolean swapped = true;
    while (gap > 1 || swapped) {
        if (gap > 1) 
            gap = (int) (gap / 1.25);

        int i = 0;
        swapped = false;
        while (i + gap < input.length) {
            if (input[i].compareTo(input[i + gap]) > 0) {
                E t = input[i];
                input[i] = input[i + gap];
                input[i + gap] = t;
                swapped = true;
            }
            i++;
        }
    }
}

Реализация на PHP[править | править код]

function combsort($array)
{
    $sizeArray = count($array);

    // Проходимся по всем элементам массива
    for ($i = 0; $i < $sizeArray; $i++) {

        // Сравниваем попарно.
        // Начинаем с первого и последнего элемента, затем постепенно уменьшаем
        // диапазон сравниваемых значеный.
        for ($j = 0; $j < $i + 1; $j++) {

            // Индекс правого элемента в текущей итерации сравнения
            $elementRight = ($sizeArray - 1) - ($i - $j);

            if ($array[$j] > $array[$elementRight]) {

                $buff                 = $array[$j];
                $array[$j]            = $array[$elementRight];
                $array[$elementRight] = $buff;
                unset($buff);

            }

        }
    }

    return $array;
}

Реализация на Python[править | править код]

def CombSort(ls):
    n = len(ls)
    step = n
    while step > 1 or flag:
       if step > 1:
           step = int(step / 1.25)
       flag, i = False, 0
       while i + step < n:
          if ls[i] > ls[i + step]:
              ls[i], ls[i + step] = ls[i + step], ls[i]
              flag = True
          i += step
    return ls

Реализация на JavaScript[править | править код]

function combSorting(array) {
  	var interval = Math.floor(array.length / 1.25);
  	while (interval > 0) {
    	for(var i = 0; i + interval < array.length; i++) {
	      	if (array[i] > array[i + interval]) {
		        var small = array[i + interval];
		        array[i + interval] = array[i];
				array[i] = small;
			}
		}
		interval = Math.floor(interval / 1.25);
	}
}

Реализация на C#[править | править код]

public static void CombSort(byte[] bytes, bool swapped = false, double factor = 1.25)
{
    ulong gap = (ulong)bytes.Length;
    
    while ((gap > 1) || swapped)
    {
        gap = (ulong)(gap / factor);
        if (gap < 1) gap = 1;
        ulong i = 0;
        ulong m = gap;
        swapped = false;
        while (m < (ulong)bytes.Length)
        {
            if (bytes[i] > bytes[m])
            {
                swapped = true;
                byte t = bytes[i];
                bytes[i] = bytes[m];
                bytes[m] = t;
            }
            i++;
            m = i + gap;
        }
    }
}

Примечания[править | править код]

  1. ↑ Lacey S., Box R. A Fast, Easy Sort: A novel enhancement makes a bubble sort into one of the fastest sorting routines (англ.) // Byte. — Апрель 1991. — Vol. 16, no. 4. — P. 315—320. — ISSN 0360-528.
Источник — https://ru.wikipedia.org/w/index.php?title=Сортировка_расчёской&oldid=136377145