Теорема Брианшона

Теорема Брианшона — классическая теорема проективной геометрии. Теорема была доказана Брианшоном в 1810 году.

Формулировка

Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.

Замечания

• Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай, приведённый ниже, двойственен к теореме Паппа.

Вырожденные случаи

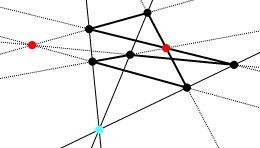
• Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.

• В произвольном треугольнике чевианы, соединяющие вершины с точкой касания противоположной стороны, пересекаются в одной точке.

Brianshon-4-1

• В описанном четырёхугольнике диагонали и прямые, соединяющие точки касания противоположных сторон, пересекаются в одной точке.

См. также

• Квадрика
• Кривая второго порядка
• Коническая константа
• Поверхность второго порядка
• Теорема Дезарга
• Теорема Паскаля

Ссылки

• Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).