SO(10)


SO(10) — разновидность теории Великого объединения, основанная на спинорной группе Spin(10)[1]. Сокращенное название SO(10) является общепринятым[2] среди физиков и происходит от группы Ли SO(10), которая является специальной ортогональной группой, дважды покрытой[англ.] Spin(10).
История[править | править код]
До теории SU(5), лежащей в основе модели Джорджи–Глэшоу[англ.][3], Харальд Фрич и Питер Минковский[англ.] и независимо Говард Джорджи обнаружили, что все содержимое материи включено в одно представление, спинорное 16 из SO(10). Однако, стоит отметить, что Джорджи нашел теорию SO(10) всего за несколько часов до того, как нашел SU(5) в конце 1973 года. [4]
Важные подгруппы[править | править код]
Она имеет правила ветвления[англ.], [SU(5)×U(1)χ]/Z5.
Если гиперзаряд содержится в SU(5), то это обычная модель Джорджи–Глэшоу[англ.], в которой 16 — поля материи, 10 -э лектрослабое поле Хиггса и 24 — в 45 — поле Хиггса ТВО. Суперпотенциал[англ.] может затем включать перенормируемые члены вида Tr(45 45); Tr(45 45 45); 10 45 10, 10 16* 16 и 16* 16. Первые три отвечают за нарушение калибровочной симметрии при низких энергиях и дают массу Хиггса, а последние два дают массы частиц материи и их взаимодействия Юкавы с Хиггсом.
Существует еще одна возможная модификация, при которой гиперзаряд представляет собой линейную комбинацию генератора SU(5) и χ. Она известна как перевёрнутая SU(5)[англ.].
Другая важная подгруппа-это либо [SU(4) × SU(2)L × SU(2)R]/Z2, либо Z2 [SU(4) × SU(2)L × SU(2)R]/Z2, в зависимости от того, нарушена ли лево-правая симметрия, что приводит к модели Пати-Салама[англ.], правило ветвления которой
Спонтанное нарушение симметрии[править | править код]
Нарушение симметрии SO(10) обычно выполняется с помощью сочетания (( a 45H OR a 54H) AND ((a 6H AND a ) OR (a 126H AND a )) ).
Допустим, мы выбираем 54H. Когда это поле Хиггса приобретает вакуммное среднее в масштабе ТВО, мы имеем нарушение симметрии до Z2 [SU(4) × SU(2)L × SU(2) R]/Z2, т. е. модель Пати-Салама[англ.] с лево-правой симметрией Z2.
Если вместо этого у нас есть 45H, это поле Хиггса может получить любое вакуммное среднее в двумерном подпространстве, не нарушая стандартную модель. В зависимости от направления этой линейной комбинации мы можем нарушить симметрию до SU(5)×U(1), модели Джорджи–Глэшоу[англ.] с U(1) (diag(1,1,1,1,1,-1,-1,-1,-1,-1)), перевёрнутой SU(5)[англ.] (diag(1,1,1,-1,-1,-1,-1,-1,1,1)), SU(4)×SU(2)×U(1) (diag(0,0,0,1,1,0,0,0,-1,-1)), минимальной лево-правой модели (diag(1,1,1,0,0,-1,-1,-1,0,0)) или SU(3)×SU(2)×U(1)×U(1) для любого другого ненулевого вакуумного среднего.
Выбор diag(1,1,1,0,0,-1,-1,-1,0,0) называется механизмом Димопулоса-Вильчека[англ.], он же "механизм отсутствия вакуумного среднего", и он пропорционален B−L.
Выбор 16H и разбивает калибровочную группу до уровня Джорджи–Глэшоу SU(5). Тот же комментарий относится к выбору ССС и DDD.
Это объединение как 45/54, так и 16/ или 126/, которое возвращает SO(10) к стандартной модели.
Электрослабый Хиггс и проблема расщепления дублета-триплета[править | править код]
Электрослабые дублеты Хиггса происходят от SO(10) 10H. К сожалению, эти же 10 также содержат тройняшки. Массы дублетов должны быть стабилизированы в электрослабом масштабе, который на много порядков меньше, чем масштаб ТВО, в то время как триплеты должны быть действительно тяжелыми, чтобы предотвратить распад протона, опосредованный триплетами. См. проблему расщепления дублета–триплета[англ.].
Среди решений для этого — механизм Димопулоса-Вильчека, или выбор diag(0,0,0,1,1,0,0,0,-1,-1) от <45>. К сожалению, он не является стабильным, так как сектор 16/ или 126/ взаимодействует с сектором 45.[5]
Содержание[править | править код]
Материя[править | править код]

Материю представляют три экземпляра (поколения) из 16 представлений. Взаимодействие Юкавы — это 10H 16f 16f. Jyj включает в себя правостороннее нейтрино. Можно либо включить три копии синглетных представлений φ и взаимодействие Юкавы ("механизм двойных качелей"); либо добавить взаимодействие Юкавы или добавить ненормируемую связь . См. механизм качелей.
Поле 16f распадается на [SU(5)×U(1)χ]/Z5 и SU(4) × SU(2)L × SU(2)R как
Калибровочные поля[править | править код]
45 полей распадаются на [SU(5)×U(1)χ]/Z5 и SU(4) × SU(2)L × SU(2)R как
и на стандартную модель [SU(3)C × SU(2)L × U(1)Y]/Z6 как
Четыре линии — это SU(3)C, SU(2)L и U(1)B−L бозоны; лептокварки SU(5), которые не изменяют заряд X[англ.]; лептокварки Пати-Салама[англ.] и бозоны SU(2)R; и новые SO(10) лептокварки. (Стандартное электрослабое взаимодействие U(1)Y представляет собой линейную комбинацию бозонов (1,1)0.)
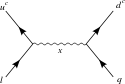
Распад протона[править | править код]
- Эти рисунки относятся к X-бозонам и бозонам Хиггса.
-
6-мерный распад протона, опосредованный X-бозоном в SU(5) ТВО
-
6-мерный распад протона, опосредованный X-бозоном в перевёрнутой SU(5) ТВО
Модель ТВО SO(10) содержит как модель Джорджи-Глэшоу SU(5), так и перевёрнутую SU(5).
Разновидность, свободная от локальных и глобальных аномалий[править | править код]
Давно известно, что модель SO(10) свободна от всех возмущающих локальных аномалий, вычислимых диаграммами Фейнмана. Однако только в 2018 году стало ясно, что SO(10) модель также свободна от всех непертурбативных глобальных аномалий[англ.] на неспиновых многообразиях --- важное правило для подтверждения согласованности теории великого объединения SO(10) со Spin(10) калибровочной группой и киральными фермионами в 16-мерных спинорных представлениях, определенных на неспиновых многообразиях[англ.]. [6][7]
См. также[править | править код]
Примечания[править | править код]
- ↑ Окунь Л. Б. Лептоны и кварки. — М., Едиториал УРСС, 2005. — с. 254
- ↑ Langacker, Paul (2012). "Grand unification". Scholarpedia. 7 (10): 11419. Bibcode:2012SchpJ...711419L. doi:10.4249/scholarpedia.11419.
- ↑ Georgi, Howard; Glashow, Sheldon (1974). "Unity of All Elementary-Particle Forces". Physical Review Letters. 32 (8): 438. Bibcode:1974PhRvL..32..438G. doi:10.1103/PhysRevLett.32.438. S2CID 9063239.
- ↑ This story is told in various places; see for example, Yukawa-Tomonaga 100th Birthday Celebration; Fritzsch and Minkowski analyzed SO(10) in 1974.
- ↑ *J.C. Baez, J. Huerta (2010). "The Algebra of Grand Unified Theories". Bull. Am. Math. Soc. 47 (3): 483—552. arXiv:0904.1556. doi:10.1090/S0273-0979-10-01294-2. S2CID 2941843.
- ↑ Wang, Juven; Wen, Xiao-Gang (1 June 2020). "Nonperturbative definition of the standard models". Physical Review Research. 2 (2): 023356. arXiv:1809.11171. Bibcode:2018arXiv180911171W. doi:10.1103/PhysRevResearch.2.023356. ISSN 2469-9896. S2CID 53346597.
- ↑ Wang, Juven; Wen, Xiao-Gang; Witten, Edward (May 2019). "A New SU(2) Anomaly". Journal of Mathematical Physics. 60 (5): 052301. arXiv:1810.00844. Bibcode:2019JMP....60e2301W. doi:10.1063/1.5082852. ISSN 1089-7658. S2CID 85543591.