Участник:AKA MBG/Направленный ациклический граф

Student 1. User:Owlunacy

Топологический порядок направленного ациклического графа: каждое ребро идет от предыдущего по порядку (верхний левый угол) к следующему (нижний правый угол). Направленный граф ациклический, если и только если у него есть топологический порядок.

В математике и информатике, направленный ациклический граф (DAG) — это конечный направленный граф без направленных циклов. Таким образом, он состоит из конечного числа вершин и ребер с концами, направленными от одной вершины к другой, такого, что невозможно начать в любой вершине v и идти за последовательно направленными ребрами, что в конечном счете снова приведет к v. Другими словами, DAG — направленный граф, у которого есть топологическое назначение, последовательность вершин которого, подбирается таким образом, что каждое ребро упорядоченно направлено от одной вершины к другой.

Направленные ациклические графы могут использоваться для моделирования многих различных видов информации. Для достижения зависимости в DAG формируется частичное упорядочивание. PERT использует DAG, чтобы смоделировать этапы и задачи больших проектов, составить график этих проектов для экономии времени. Планирование компьютерных операций, таких как обновления электронной таблицы или операции по компиляции в утилите может выполняться с применением топологического упорядочивания DAG. Комбинационные логические блоки в дизайне электронной схемы и операции на языках программирования потока информации, включают ациклические сети обработки элементов. DAG может также представлять коллекции событий и их влияния друг на друга, либо в вероятностной структуре, такой, как Байесовская сеть или отчет исторических данных, таких, как родословные или интерпретации распределенных систем управления ревизией. DAG могут также использоваться в качестве компактного представления данных о последовательности, таких как направленный ациклический словесный граф, представляющий коллекции последовательностей или представление бинарной схемы принятия решений последовательностей двойного выбора.

Важные полиномиальные вычислительные задачи на DAG включают топологическую сортировку (топологическое упорядочивание), построение транзитивных сокращений и транзитивных замыканий и задачу связи, цель которой состоит в том, чтобы найти подмножество с минимальным весом вершин графа без ребер, соединяющих их с остальной частью графа. Преобразование направленного графа с циклами в DAG, с удалением как можно меньшего числа вершин или ребер — это NP-полная задача, но любой направленный граф может быть превращен в DAG (уменьшением объёма), посредством сокращения каждого сильно связанного компонента в одну «супервершину». Проблемы нахождения кратчайших путей и самых длинных путей могут быть решены на DAG в линейное время, в отличие от произвольных графов, для которых алгоритмы нахождения кратчайшего пути работают медленнее, а нахождение самых длинных путей является NP-полной задачей.

Соответствующее понятие для ненаправленных графов — лес, ненаправленный граф без циклов. Выбор ориентации для леса образует специальный вид направленного ациклического графа, названного «полидеревом». Однако, есть много других видов направленного ациклического графа, у которых не сформированы ориентиры ребер ненаправленного ациклического графа. Кроме того, у каждого ненаправленного графа есть ациклическая ориентация и назначение направления для его ребер, которое превращает его в направленный ациклический граф. Чтобы подчеркнуть отличие DAG от направленных версий ненаправленных ациклических графов, некоторые авторы называют их ациклическими направленными графами или ациклическими диграфами.

Определения

Student 2. User:Remediassance

Граф — это совокупность непустого множества вершин и ребер, в котором вершины представляют собой попарно соединенные ребрами объекты, не имеющие структуры. В случае ориентированного графа (орграфа), каждое ребро имеет направленную связь от одной вершины к другой. Путем в ориентированном графе называется последовательность вершин, имеющая для каждой вершины ребро, соединяющее её со следующей вершиной в последовательности. Путь является циклом, если совпадают его начальная и конечная вершины. Направленным ациклическим графом называется ориентированный граф, не имеющий циклов.

Добавление красных ребер к синему ориентированному ациклическому графу создает новый ОАГ, транзитивное замыкание синего графа. Для каждого красного или синего ребра uv, v достижимо из u: существует синий путь, берущий начало в u и заканчивающийся в v.

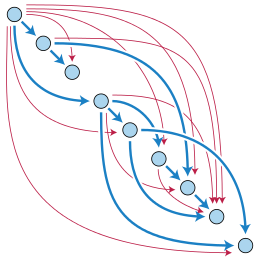
Вершина v ориентированного графа достижима из вершины u, если есть путь, начинающийся в u и заканчивающийся в v. Следовательно, любая вершина достижима из самой себя (путем из 0 ребер). Если в вершину можно попасть нетривиальным путем (содержащим хотя бы одно ребро), тогда этот путь является циклом. Таким образом, сущестует другое определение направленного ациклического графа — это граф, в котором ни одна вершина не может достичь саму себя нетривиальным путем.

Топологическая сортировка ориентированного графа — это расположение его вершин в форме последовательности, такой, что для каждого ребра начальная вершина ребра встречается в последовательности раньше, чем конечная вершина ребра. Граф, у которого есть топологическая сортировка, не может иметь циклов, потому что ребро, связанное с самой первой вершиной в цикле, должно бы было быть направлено не в ту сторону. Таким образом, каждый граф с топологической сортировкой ациклический. И напротив, каждый ориентированный ациклический граф имеет топологическую сортировку. Таким образом, это свойство может быть использовано как альтернативное определение ориентированных ациклических графов: это именно те графы, которые имеют топологические сортировки.

Mathematical properties

Reachability, transitive closure, and transitive reduction

Student 3. User:Remediassance

The reachability relationship in any directed acyclic graph can be formalized as a partial order ≤ on the vertices of the DAG. In this partial order, two vertices u and v are ordered as u ≤ v exactly when there exists a directed path from u to v in the DAG; that is, when v is reachable from u. However, different DAGs may give rise to the same reachability relation and the same partial order. For example, the DAG with two edges a → b and b → c has the same reachability relation as the graph with three edges a → b, b → c, and a → c. Both of these DAGS produce the same partial order, in which the vertices are ordered as a ≤ b ≤ c.

If G is a DAG, its transitive closure is the graph with the most edges that represents the same reachability relation. It has an edge u → v whenever u can reach v. That is, it has an edge for every related pair u ≤ v of distinct elements in the reachability relation of G, and may therefore be thought of as a direct translation of the reachability relation ≤ into graph-theoretic terms. The same method of translating partial orders into DAGs works more generally: for every finite partially ordered set (S, ≤), the graph that has a vertex for each member of S and an edge for each pair of elements related by u ≤ v is automatically a transitively closed DAG, and has (S, ≤) as its reachability relation. In this way, every finite partially ordered set can be represented as the reachability relation of a DAG.

The transitive reduction of a DAG G is the graph with the fewest edges that represents the same reachability relation as G. It is a subgraph of G, formed by discarding the edges u → v for which G also contains a longer path connecting the same two vertices. Like the transitive closure, the transitive reduction is uniquely defined for DAGs. In contrast, for a directed graph that is not acyclic, there can be more than one minimal subgraph with the same reachability relation.

A Hasse diagram representing the partial order of set inclusion (⊆) among the subsets of a three-element set.

If a DAG G has a reachability relation described by the partial order ≤, then the transitive reduction of G is a subgraph of G that has an edge u → v for every pair in the covering relation of ≤. Transitive reductions are useful in visualizing the partial orders they represent, because they have fewer edges than other graphs representing the same orders and therefore lead to simpler graph drawings. A Hasse diagram of a partial order is a drawing of the transitive reduction in which the orientation of each edge is shown by placing the starting vertex of the edge in a lower position than its ending vertex.

Топологическая сортировка

Student 4. User:Remediassance

Каждый ориентированный ациклический граф имеет топологическую сортировку, сортировку вершин, такую, что начальная вершина каждого ребра встречается в сортировке раньше, чем конечная вершина ребра. Существование такой сортировки может быть использовано, чтобы охарактеризовать ОАГ: ориентированный граф является ОАГ тогда и только тогда, когда у него есть топологическая сортировка. В общем случае, эта сортировка не уникальна; ОАГ имеет уникальную топологическую сортировку тогда и только тогда, когда в нём есть ориентированный путь, содержащий все вершины, в случае чего сортировка совпадает с порядком, в котором вершины появляются в этом пути.

Семейство топологических сортировок ОАГ такое же, как и семейство линейных расширений отношения достижимости для ОАГ, так что любые два графа, в одинаковой степени частично упорядоченные, имеют одинаковое множество топологических порядков.

Комбинаторное перечисление

Student 5. User:Sergei.podkopaev

Задача перечисления графов, а точнее, задача о подсчёте всех возможных направленных графов без циклов изучалась Робинсоном (Robinson (1973)). Количество ориентированных ациклических графов из n помеченных вершин, для n = 0, 1, 2, 3, … (без ограничений на порядок, в котором эти числа появляются в топологически отсортированном DAG)

1, 1, 3, 25, 543, 29281, 3781503, … последовательность A003024 в OEIS.

Эти числа могут быть вычислены по рекуррентной формуле

$a_{n}=\sum _{k=1}^{n}(-1)^{k-1}{n \choose k}2^{k(n-k)}a_{n-k}$.

Эрик В. Вайстайн предположил, и МакКей (McKay et al. (2004)) доказал, что эти же числа посчитанные бинарной матрицей для которых все собственные векторы — положительные вещественные числа. Биективное доказательство: матрица A — матрица смежности DAG тогда и только тогда, когда A + I — бинарная матрица со всеми положительными собственными значениями, где I обозначает единичную матрицу. Так как DAG не может иметь петель, то матрица смежности должна содержать нули на главной диагонали, таким образом, добавление I сохраняет свойство, что все коэффициенты матрицы равны либо 0 либо 1.

Related families of graphs

Student 6. User:Sergei.podkopaev

A polytree is a directed graph formed by orienting the edges of a free tree. Every polytree is a DAG. In particular, this is true of the arborescences formed by directing all edges outwards from the roots of a tree.

A multitree (also called a strongly unambiguous graph or a mangrove) is a directed graph in which there is at most one directed path (in either direction) between any two vertices; equivalently, it is a DAG in which, for every vertex v, the subgraph reachable from v forms a tree.

Computational problems

Topological sorting and recognition

Student 7. User:Sergei.podkopaev

Основная статья: Topological sorting

Topological sorting is the algorithmic problem of finding a topological ordering of a given DAG. It can be solved in linear time. Kahn’s algorithm for topological sorting builds the vertex ordering directly. It maintains a list of vertices that have no incoming edges from other vertices that have not already been included in the partially constructed topological ordering; initially this list consists of the vertices with no incoming edges at all. Then, it repeatedly adds one vertex from this list to the end of the partially constructed topological ordering, and checks whether its neighbors should be added to the list. The algorithm terminates when all vertices have been processed in this way. Alternatively, a topological ordering may be constructed by reversing a postorder numbering of a depth-first search graph traversal.

It is also possible to check whether a given directed graph is a DAG in linear time, either by attempting to find a topological ordering and then testing for each edge whether the resulting ordering is valid or alternatively, for some topological sorting algorithms, by verifying that the algorithm successfully orders all the vertices without meeting an error condition.

Construction from cyclic graphs

Student 8. User:kanphis

Any undirected graph may be made into a DAG by choosing a total order for its vertices and directing every edge from the earlier endpoint in the order to the later endpoint. The resulting orientation of the edges is called an acyclic orientation. Different total orders may lead to the same acyclic orientation, so an n-vertex graph can have fewer than n! acyclic orientations. The number of acyclic orientations is equal to |χ(−1)|, where χ is the chromatic polynomial of the given graph.

The yellow directed acyclic graph is the condensation of the blue directed graph. It is formed by contracting each strongly connected component of the blue graph into a single yellow vertex.

Any directed graph may be made into a DAG by removing a feedback vertex set or a feedback arc set, a set of vertices or edges (respectively) that touches all cycles. However, the smallest such set is NP-hard to find. An arbitrary directed graph may also be transformed into a DAG, called its condensation, by contracting each of its strongly connected components into a single supervertex. When the graph is already acyclic, its smallest feedback vertex sets and feedback arc sets are empty, and its condensation is the graph itself.

Transitive closure and transitive reduction

Student 9. User:kanphis

The transitive closure of a given DAG, with n vertices and m edges, may be constructed in time O(mn) by using either breadth-first search or depth-first search to test reachability from each vertex. Alternatively, it can be solved in time O(n^ω) where ω < 2.373 is the exponent for fast matrix multiplication algorithms; this is a theoretical improvement over the O(mn) bound for dense graphs.

In all of these transitive closure algorithms, it is possible to distinguish pairs of vertices that are reachable by at least one path of length two or more from pairs that can only be connected by a length-one path. The transitive reduction consists of the edges that form length-one paths that are the only paths connecting their endpoints. Therefore, the transitive reduction can be constructed in the same asymptotic time bounds as the transitive closure.

Closure problem

Student 10. User:username

Основная статья: Closure problem

The closure problem takes as input a directed acyclic graph with weights on its vertices and seeks the minimum (or maximum) weight of a closure, a set of vertices with no outgoing edges. (The problem may be formulated for directed graphs without the assumption of acyclicity, but with no greater generality, because in this case it is equivalent to the same problem on the condensation of the graph.) It may be solved in polynomial time using a reduction to the maximum flow problem.

Path algorithms

Some algorithms become simpler when used on DAGs instead of general graphs, based on the principle of topological ordering. For example, it is possible to find shortest paths and longest paths from a given starting vertex in DAGs in linear time by processing the vertices in a topological order, and calculating the path length for each vertex to be the minimum or maximum length obtained via any of its incoming edges. In contrast, for arbitrary graphs the shortest path may require slower algorithms such as Dijkstra's algorithm or the Bellman–Ford algorithm, and longest paths in arbitrary graphs are NP-hard to find.

Applications

Scheduling

Student 11. User:username

Directed acyclic graphs representations of partial orderings have many applications in scheduling for systems of tasks with ordering constraints. An important class of problems of this type concern collections of objects that need to be updated, such as the cells of a spreadsheet after one of the cells has been changed, or the object files of a piece of computer software after its source code has been changed. In this context, a dependency graph is a graph that has a vertex for each object to be updated, and an edge connecting two objects whenever one of them needs to be updated earlier than the other. A cycle in this graph is called a circular dependency, and is generally not allowed, because there would be no way to consistently schedule the tasks involved in the cycle. Dependency graphs without circular dependencies form DAGs.

For instance, when one cell of a spreadsheet changes, it is necessary to recalculate the values of other cells that depend directly or indirectly on the changed cell. For this problem, the tasks to be scheduled are the recalculations of the values of individual cells of the spreadsheet. Dependencies arise when an expression in one cell uses a value from another cell. In such a case, the value that is used must be recalculated earlier than the expression that uses it. Topologically ordering the dependency graph, and using this topological order to schedule the cell updates, allows the whole spreadsheet to be updated with only a single evaluation per cell. Similar problems of task ordering arise in makefiles for program compilation and instruction scheduling for low-level computer program optimization.

PERT chart for a project with five milestones (labeled 10-50) and six tasks (labeled A-F). There are two critical paths, ADF and BC.

A somewhat different DAG-based formulation of scheduling constraints is used by the program evaluation and review technique (PERT), a method for management of large human projects that was one of the first applications of DAGs. In this method, the vertices of a DAG represent milestones of a project rather than specific tasks to be performed. Instead, a task or activity is represented by an edge of a DAG, connecting two milestones that mark the beginning and completion of the task. Each such edge is labeled with an estimate for the amount of time that it will take a team of workers to perform the task. The longest path in this DAG represents the critical path of the project, the one that controls the total time for the project. Individual milestones can be scheduled according to the lengths of the longest paths ending at their vertices.

Сети обработки данных

Student 12. User:Bonch-Bonch

Направленный ациклический граф может быть использован для представления сети обрабатывающих элементов. В этом представлении данные поступают в обрабатывающий элемент через свои входящие ребра и покидают элемент через исходящие ребра.

Например, в электронной схеме, статические комбинационные логические блоки могут быть представлены в виде ациклической системы логических вентилей, которые вычисляют функцию входа. Вход и выход функции представлены как отдельные биты. В общем, выход из этих блоков не может быть использован в качестве входного сигнала, если он не захватывается регистром или запоминающимся элементом, который сохраняет свои ациклические свойства. Электронные контурные схемы на бумаге или в базе данных являются одной из форм направленных ациклических графов с использованием экземпляров или компонентов для формирования направленной ссылки на более низком уровне компонента. Сами электронные схемы не обязательно являются ациклическими или направленными.

Языки программирования DataFlow описывают системы операций на потоках данных, а также соединения между выходами некоторых операций и входами других. Эти языки могут быть удобны для описания повторяющихся задач обработки данных, в которых тот же ациклически соединенный набор операций применяется ко многим видам элементов данных. Они могут быть выполнены в виде параллельного алгоритма, в котором каждая операция выполняется параллельным процессом, как только ещё один набор входов становится доступным для него.

В компиляторах, прямолинейный код (то есть последовательность операторов без петель или условных ветвей) может быть представлен в группе DAG с описанием входов и выходов каждого из арифметических операций, выполняемых в коде. Это представление позволяет компилятору эффективно выполнять удаление общих подвыражений.

Causal structures

Student 13. User:username

Основная статья: Bayesian network

Graphs in which vertices represent events occurring at a definite time, and where the edges are always point from the early time vertex to a late time vertex of the edge, are necessarily directed and acyclic. The lack of a cycle follows because the time associated with a vertex always increases as you follow any path in the graph so you can never return to a vertex on a path. This reflects our natural intuition that causality means events can only affect the future, they never affect the past, and thus we have no causal loops. An example of this type of directed acyclic graph are those encountered in the causal set approach to quantum gravity though in this case the graphs considered are transitively complete. The version history example, each version of the software is associated with a unique time, typically the time the version was saved, committed or released. For citation graphs, the documents are published at one time and can only refer to older documents.

Sometimes events are not associated with a specific physical time. Provided that pairs of events have a purely causal relationship, that is edges represent represent causal relations between the events, we will have a directed acyclic graph. For instance, a Bayesian network represents a system of probabilistic events as vertices in a directed acyclic graph, in which the likelihood of an event may be calculated from the likelihoods of its predecessors in the DAG. In this context, the moral graph of a DAG is the undirected graph created by adding an (undirected) edge between all parents of the same vertex (sometimes called marrying), and then replacing all directed edges by undirected edges. Another type of graph with a similar causal structure is an influence diagram, the vertices of which represent either decisions to be made or unknown information, and the edges of which represent causal influences from one vertex to another. In epidemiology, for instance, these diagrams are often used to estimate the expected value of different choices for intervention.

The converse is also true. That is in any application represented by a directed acyclic graph there is a causal structure, either an explicit order or time in the example or an order can be derived from the which can be derived from graph structure. This follows because all directed acyclic graphs have a topological ordering, i.e. there is at least one way to put the vertices in an order such that all edges point in the same direction along that order.

Genealogy and version history

Student 14. User:username

Family tree of the Ptolemaic dynasty, with many marriages between close relatives causing pedigree collapse

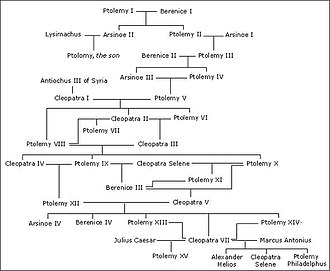
Family trees may be seen as directed acyclic graphs, with a vertex for each family member and an edge for each parent-child relationship. Despite the name, these graphs are not necessarily trees because of the possibility of marriages between relatives (so a child has a common ancestor on both the mother’s and father’s side) causing pedigree collapse. The graphs of matrilineal descent («mother» relationships between women) and patrilineal descent («father» relationships between men) are trees within this graph. Because no one can become their own ancestor, family trees are acyclic.

For the same reason, the version history of a distributed revision control system generally has the structure of a directed acyclic graph, in which there is a vertex for each revision and an edge connecting pairs of revisions that were directly derived from each other. These are not trees in general due to merges.

In many randomized algorithms in computational geometry, the algorithm maintains a history DAG representing the version history of a geometric structure over the course of a sequence of changes to the structure. For instance in a randomized incremental algorithm for Delaunay triangulation, the triangulation changes by replacing one triangle by three smaller triangles when each point is added, and by «flip» operations that replace pairs of triangles by a different pair of triangles. The history DAG for this algorithm has a vertex for each triangle constructed as part of the algorithm, and edges from each triangle to the two or three other triangles that replace it. This structure allows point location queries to be answered efficiently: to find the location of a query point q in the Delaunay triangulation, follow a path in the history DAG, at each step moving to the replacement triangle that contains q. The final triangle reached in this path must be the Delaunay triangle that contains q.

Citation graphs

Student 15. User:Bonch-Bonch

In a citation graph the vertices are documents with a single publication date. The edges represent the citations from the bibliography of one document to other necessarily earlier documents. The classic example comes from the citations between academic papers as pointed out in the 1965 article «Networks of Scientific Papers» by Derek J. de Solla Price. In this case the citation count of a paper is just the in-degree of the corresponding vertex of the citation network. This is an important measure in citation analysis. Court judgements provide another example as judges support their conclusions in one case by recalling other earlier decisions made in previous cases. A final example is provided by patents which must refer to earlier prior art, earlier patents which are relevant to the current patent claim. By taking the special properties of directed acyclic graphs into account, one can analyse these graphs with techniques not available when analysing the general graphs considered in many studies in network analysis. For instance transitive reduction gives a new insights into the citation distributions found in different applications highlighting clear differences in the mechanisms creating citations networks in different contexts.

Сжатие данных

Student 16. User:kanphis

Также направленный ациклический граф можно использовать для компактного представления коллекции последовательностей. В этой задаче нужно построить такой DAG, чтобы пути в нём соответствовали заданным последовательностям. Если у многих последовательностей есть общие подпоследовательности, то в DAG им соответствуют общие вершины и ребра. При таком подходе представление коллекции последовательностей в виде DAG занимает меньше места, чем полный список всех последовательностей.

С помощью DAG можно также представить и префиксное дерево. Узлы помечаются буквами, и пути от корней до листьев представляют одно слово или строку. Пути для слов с одинаковыми приставками, корнями или суффиксами в своем представлении могут пересекаться, то есть, использовать одни и те же вершины и ребра для одинаковых частей слов.

Та же идея представления в DAG семейства путей использована в бинарной диаграмме решений, форме представления булевых функций. В бинарной диаграмме решений каждая не конечная вершина помечена названием бинарной переменной, а каждое ребро помечены числами 0 или 1 — значениями соответствующих переменных. Листы помечены числами 0 или 1 — значениями функции при значениях переменных при пути от корня до листа. Так же, как и в случае с префиксным деревом, бинарную диаграмму решений можно рассматривать как сжатую форму представления дерева принятия решений, так как пути в них могут сходиться и расходиться.

External links

• Weisstein, Eric W. Acyclic Digraph (англ.) на сайте Wolfram MathWorld.

Категория:Теория графов Категория:Структуры данных