Дискретизация

Дискретизация непрерывного аналогового сигнала. Выборки изображены точками на кривой. Период дискретизации обозначен $T$.

См. также: Дискретность

Дискретиза́ция (от лат. discretio — «различать», «распознавать») — в общем случае — представление непрерывной функции дискретной совокупностью её значений при разных наборах аргументов. Для функции переменной $f(x)$ — представление её множеством $n$ её значений $f(x_{0}),f(x_{1}),...f(x_{n-1})$ на заданном дискретном множестве значений аргумента $x_{0},x_{1},...x_{n-1}$.

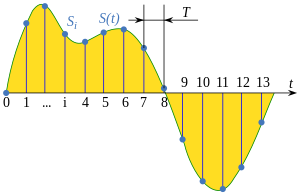
В обработке сигналов — представление аналогового непрерывного сигнала $S(t)$ совокупностью его значений, эту совокупность принято называть выборками $S(t_{0}),S(t_{1}),...S(t_{n-1})$, взятых в моменты времени $t_{0},t_{1},...t_{n-1}$.

В общем случае период времени от одной выборки до следующей может различаться для каждой пары соседних выборок, но обычно при обработке сигнала, выборки следуют через фиксированный и постоянный промежуток времени. Этот промежуток в таком случае называют периодом дискретизации или интервалом выборок и обычно обозначается буквой $T$. Величину обратную периоду дискретизации $F_{s}=1/T$ называют частотой выборок или частотой дискретизации.

Примерами аналогового сигнала могут служить аудио- или видеосигналы, сигналы различных измерительных датчиков и др. Для последующей цифровой обработки аналоговые непрерывные сигналы обязательно предварительно подвергаются дискретизации и квантованию по уровню с помощью аналого-цифровых преобразователей.

Обратный процесс получения непрерывного аналогового сигнала, заданного дискретной совокупностью его выборок, называется восстановлением. Восстановление производится цифро-аналоговыми преобразователями.

Теория

Дискретизация гребёнкой Дирака

В математических терминах — дискретизация это умножение непрерывной функции $s(t)$ на функцию, называемую гребень Дирака $\Delta _{T}(t)\ {\stackrel {\mathrm {def} }{=}}\ \sum _{k=-\infty }^{\infty }\delta (t-kT)$ где $T$ — константа — период дискретизации и $\delta (t)$ — дельта-функция Дирака:

$s_{\mathrm {a} }(t)=s(t)\cdot \sum _{n=-\infty }^{\infty }\delta (t-nT).$

Преобразование Фурье дискретной функции $s_{\mathrm {a} }(t)$ даёт её спектр $S_{\mathrm {a} }(f)$. Согласно теореме Котельникова, если спектр $S(f)$ исходной функции ограничен, то есть спектральная плотность нулевая свыше некоторой частоты $f_{max}$, то исходная функция однозначно восстановима по совокупности её выборок, взятых с частотой дискретизации $1/T\geq 2f_{max}$.

Для абсолютно точного восстановления необходимо подать на вход идеального фильтра нижних частот последовательность бесконечно коротких импульсов каждый с площадью равной значению выборки.

Практически невозможно идеально точно восстановить реальные сигналы по выборкам, так как во-первых, не существует сигналов с ограниченным спектром, ибо реальные сигналы ограничены во времени, что обязательно даёт спектр бесконечной ширины. Во-вторых, физически нереализуем идеальный фильтр низких частот (sinc-фильтр), в третьих, невозможны бесконечно короткие импульсы с конечной площадью.

Применение

Все сигналы в природе по сути аналоговые. Для цифровой обработки сигнала, хранения его и передачи в цифровом виде аналоговые сигналы предварительно оцифровываются. Оцифровка включает дискретизацию и квантование по уровню, производимую с помощью АЦП. После цифровой обработки, передачи, хранения цифровых данных, кодирующих сигнал, часто необходимо обратное преобразование цифрового образа сигнала в аналоговый сигнал. Например, звуковоспроизведение аудиозаписей с компакт-диска.

Также дискретизация применяется в системах аналоговой импульсной модуляции.

Практически восстановление аналогового сигнала по совокупности выборок производится с той или иной степенью точности, причём точность восстановления тем выше, чем выше частота дискретизации и число уровней квантования каждой выборки. Но чем больше частота дискретизации и число уровней квантования, тем больше требуется ресурсов для обработки, хранения, передачи оцифрованных данных. Поэтому частоту дискретизации и разрядность АЦП практически выбирают исходя из разумного компромисса.

Например, при цифровой передаче голоса для хорошей разборчивости речи достаточна частота дискретизации 8 кГц.

Высококачественное воспроизведение музыкальных произведений с компакт-дисков (CD) в современном стандарте производится с частотой дискретизации 44,1 кГц (CD), 48 кГц, 88,2 кГц или 96 кГц, что обеспечивает высококачественное воспроизведение звука во всей полосе слышимых частот 20 Гц — 20 кГц.

Оцифровка телевизионного видеосигнала с полосой частот 6 МГц производится с частотой дискретизации свыше 10 МГц.

См. также

• Частота дискретизации
• Цифровой сигнал
• Квантование (обработка сигналов)
• Аналого-цифровой преобразователь
• Цифро-аналоговый преобразователь

Литература

• Самофалов К. Г., Романкевич А. М., Валуйский В. Н., Каневский Ю. С., Пиневич М. М. Прикладная теория цифровых автоматов. — Киев: Вища школа, 1987. — 375 с.

Ссылки

• Квантование сигнала — статья из Большой советской энциклопедии. 
• Sampling of analog signals Интерактивная презентация дискретизации по времени. Institute of Telecommunications, University of Stuttgart