Дельта-функция

Де́льта-фу́нкция (или дельта-мера, δ-функция, δ-функция Дирака, дираковская дельта, единичная импульсная функция) — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенных или приложенных в одной точке.
Например, плотность единичной точечной массы m, находящейся в точке a одномерного евклидова пространства записывается с помощью -функции в виде Дельта-функция также применима для описания распределений заряда, массы и т. п. на поверхностях или линиях.
Несмотря на распространённую форму записи -функция не является функцией вещественной переменной, а определяется как обобщённая функция: непрерывный линейный функционал на пространстве дифференцируемых функций. Можно ввести производную для δ-функции, которая тоже будет обобщённой функцией, и интеграл, определяемый как функция Хевисайда. Нетрудно указать последовательности обычных классических функций, слабо сходящиеся к -функции.
Можно различать одномерную и многомерные дельта-функции, однако последние могут быть представлены в виде произведения одномерных функций в количестве, равном размерности пространства, на котором определена многомерная функция.
Введена английским физиком Полем Дираком.
Определения[править | править код]
Существуют различные взгляды на понятие дельта-функции. Получающиеся при этом объекты, строго говоря, различны, однако обладают рядом общих характерных свойств. Все указанные ниже конструкции естественно обобщаются на случаи пространств большей размерности .
Простое определение[править | править код]
Дельта-функцию (функция Дирака) одной вещественной переменной можно определить как функцию , удовлетворяющую следующим условиям:
То есть эта функция не равна нулю только в точке , где она обращается в бесконечность таким образом, чтобы её интеграл по любой окрестности был равен 1. В этом смысле понятие дельта-функции аналогично физическим понятиям точечной массы или точечного заряда. Для понимания интеграла полезно представить себе некую фигуру на плоскости с единичной площадью, например, треугольник. Если уменьшать основание данного треугольника и увеличивать высоту так, чтобы площадь была неизменной, то в предельном случае мы получим треугольник с малым основанием и очень большой высотой. По предположению его площадь равна единице, что и показывает интеграл. Вместо треугольника можно без ограничения общности использовать любую фигуру. Аналогичные условия верны и для дельта-функций, определённых на
Эти равенства не принято считать определением дельта-функции, однако во многих учебниках по физике она определяется именно так, и этого достаточно для точного определения дельта-функции. Отметим, что из данного определения дельта-функции вытекает следующее равенство
(фильтрующее свойство) для любой функции f. Действительно, в силу свойства при значение этого интеграла не изменится, если функцию заменить функцией , которая равна в точке , а в остальных точках имеет произвольные значения. Например, берём , затем выносим за знак интеграла и, используя второе условие в определении дельта-функции, получаем нужное равенство.
Производные от дельта-функции также почти всюду равны 0 и обращаются в при .
Классическое определение[править | править код]
Дельта-функция определяется как линейный непрерывный функционал на некотором функциональном пространстве (пространстве основных функций). В зависимости от цели и желаемых свойств, это может быть пространство функций с компактным носителем, пространство функций, быстро убывающих на бесконечности, гладких функций на многообразии, аналитических функций и т. д. Для того, чтобы были определены производные дельта-функции с хорошими свойствами, во всех случаях основные функции берутся бесконечно дифференцируемыми, пространство основных функций также должно быть полным метрическим пространством. Общий подход к обобщённым функциям см. в соответствующей статье. Такие обобщённые функции также называют распределениями.
Мы рассмотрим самый простой вариант. В качестве пространства основных функций рассмотрим пространство всех бесконечно дифференцируемых функций на отрезке. Последовательность сходится к , если на любом компакте функции сходятся к равномерно вместе со всеми своими производными:
Это локально выпуклое метризуемое пространство. Дельта-функцию определим как функционал , такой что
Непрерывность означает, что если , то . Здесь — значение функционала на функции .
Дельта-функция по Коломбо[править | править код]
Используемому для работы с дельта-функцией интегральному выражению можно придать смысл, близкий к интуитивному, в рамках теории алгебры обобщённых функций Коломбо (англ. Colombeau algebra)[1].
Пусть — множество бесконечно дифференцируемых функций с компактным носителем, то есть не равных нулю лишь на ограниченном множестве. Рассмотрим множество функций
Обобщённая функция — это класс эквивалентности функций бесконечно дифференцируемых по x при каждом и удовлетворяющих некоторому условию умеренности (полагая и все её производные по x достаточно медленно растут при ). Две функции полагаются эквивалентными, если , где — ещё один класс функций с ограничениями на рост при
Дельта-функция определяется как Преимущество подхода Коломбо в том, что его обобщённые функции образуют коммутативную ассоциативную алгебру, при этом на множество обобщённых функций естественно продолжаются понятия интегрирования, дифференцирования, пределов, даже значения в точке. В этом смысле на дельта-функцию действительно можно смотреть как на функцию, равную 0 везде, кроме точки 0, и равную бесконечности в нуле, так как теория Коломбо включает в себя теорию бесконечно больших и бесконечно малых чисел, аналогично нестандартному анализу.
Подход Егорова[править | править код]
Аналогичная теория обобщённых функций была изложена в работе Ю. В. Егорова[2]. Хотя она не эквивалентна теории Коломбо, конструкция значительно проще и обладает большинством желаемых свойств.
Обобщённая функция — это класс эквивалентности последовательностей Последовательности и считаются эквивалентными, если для любого компакта функции последовательностей совпадают на начиная с некоторого номера:
Всевозможные операции над последовательностями (умножение, сложение, интегрирование, дифференцирование, композиция, …) определяются покомпонентно. Например, интеграл по множеству I определяется как класс эквивалентности последовательности
Две обобщённые функции слабо равны, если для любой бесконечно гладкой функции
При этом дельта-функция определяется любой дельта-образной последовательностью (см. ниже), все такие обобщённые функции слабо равны.
Свойства[править | править код]
- Дельта-функция чётная.
- Интеграл от дельта-функции по любому интервалу, содержащему в себе ноль, то есть интервалу вида где и — произвольные действительные положительные числа, равен 1.
- , где — простые нули функции .

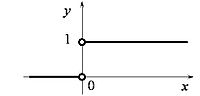
- Первообразной одномерной дельта-функции является функция Хевисайда:
- Фильтрующее свойство дельта-функции:
δ-Функция как слабый предел[править | править код]
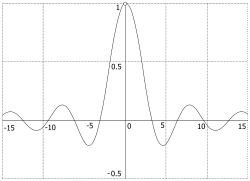
Пусть
Тогда последовательность
слабо сходится к -функции.
Выбор интегрируемой функции определённый интеграл которой в пределах от до равен 1 произволен.
Например, в качестве можно выбрать функцию sinc: дающую последовательность:
При требовании, чтобы все функции в последовательности были всюду положительны, можно в качестве исходной функции выбрать, например, нормированную функцию Гаусса или иную любую всюду неотрицательную функцию, интеграл которой равен 1:
Интегральное представление[править | править код]
Во многих приложениях оказывается удобным интегральное представление дельта-функции:
Рассмотрим интеграл
- (1)
который можно интерпретировать как предел
где
- (2)
Известно, что
- (3)
В силу (3) для любого справедливо равенство:
- (4)
Можно показать (см. выше), что при неограниченном росте N для функции (2) оказываются верными все свойства дельта-функции и она в некотором смысле стремится к
Производная дельта-функции[править | править код]
По определению производной дельта-функции :
(распространение интегрирования по частям на случай подынтегральных выражений, содержащих дельта-функцию).
Аналогично для n-й производной дельта-функции:
А проинтегрировав так по частям n раз, получим в конце концов:
Для производной дельта-функции имеет место тождество:
которое можно получить дифференцируя произведение .
Преобразование Фурье[править | править код]
- В этом параграфе мы будем применять нормировку, соответствующую соглашению о единичном коэффициенте в обратном преобразовании, то есть имея в виду
- Формулы этого параграфа имеют соответствующие аналоги для многомерного преобразования Фурье.
К дельта-функции можно применить преобразование Фурье:
Таким образом, спектр (Фурье-образ) дельта-функции, центрированной в точке , является «волной» в пространстве частот, обладающей «периодом» . В частности, спектр (Фурье-образ) дельта-функции, центрированной в нуле, является константой (нестрого говоря — «волной» с бесконечно большим «периодом»):
Соответственно, наоборот — дельта-функция является Фурье-образом чистой гармонической функции или константы.
Представление многомерных дельта-функций в различных системах координат[править | править код]
В n-мерном пространстве в декартовых координатах (ортонормированном базисе):
В двумерном пространстве:
В полярных координатах:
- — несмещённая относительно начала координат (с особенностью при r=0),
- — с особенностью в точке общего положения при r=0 доопределяется нулём.
В трёхмерном пространстве:
В цилиндрической системе координат:
- — несмещённая относительно начала координат (с особенностью при ),
- — с особенностью в точке общего положения при r=0 доопределяется нулём.
В сферической системе координат:
- — несмещённая относительно начала координат (с особенностью при r=0).
- В формулах с особенностью в начале координат нередко используют вдвое большие коэффициенты (1/π для цилиндрической и полярной, 1/2π для сферической). Это связано с тем, что предполагается вдвое меньший результат интегрирования в случае, если особая точка находится точно на границе интервала интегрирования.
Физическая интерпретация[править | править код]
Вблизи заряженной точки поле бесконечно, ряды Тейлора для поля не сходятся, поэтому вводят специальные функции. Одной из таких функций является дельта-функция. Вопрос о поле точечной заряженной частицы сравнительно сложен, поэтому рассмотрим сначала более простой пример.
Мгновенное ускорение[править | править код]
Пусть частица, способная перемещаться вдоль прямой, при ударе пренебрежимо малой длительности скачком приобретает какую-то скорость. Зададимся вопросом: как рассчитать ускорение, приобретённое телом? Построим график зависимости изменения скорости от времени. График будет иметь следующий вид:
Данный график почти всюду является графиком функции Хевисайда. Производная функции Хевисайда является единичной дельта-функцией, график которой условно можно изобразить как
Данный график отображает бесконечное ускорение при мгновенном наборе скорости. В общем случае ускорение при ударе можно записать как
Масса/заряд материальной точки[править | править код]
Если нужно найти суммарную массу (суммарный заряд) некоторого распределения плотности (или плотности заряда), содержащего, наряду с непрерывной компонентой , ещё и точечные массы (заряды), то удобно вместо формулы, раздельно учитывающей непрерывную конечную плотность и дискретные вклады:
- ,
где — радиус-вектор положения рассматриваемого элемента (для определённости обозначения соответствуют массе, а не заряду), писать просто:
- ,
имея в виду, что включает как непрерывную, так и дельтообразные, то есть сосредоточенные в геометрических точках (по одной для каждого точечного объекта ), составляющие:
- .
Другие примеры[править | править код]
- Дельта-функция применяется в математической физике при решении задач, в которые входят сосредоточенные величины. В квазиклассическом пределе () квантовой механики волновые функции локализуются в волновые пакеты с дельтообразными (то есть имеющими в пределе форму дельта-функции) огибающими, и области их локализации движутся по классическим траекториям согласно уравнениям Ньютона.
- Преобразование Фурье единицы является дельта-функцией. Это позволяет более удобно и математически строго формулировать различные задачи, связанные с преобразованием Фурье, которые очень многочисленны: волновая оптика, акустика, теория колебаний. В квантовой механике преобразования Фурье волновых функций играют первостепенную принципиальную и техническую роль, именно для неё Дирак впервые ввёл дельта-функцию.
- Дельта-функции играют роль собственных функций оператора с непрерывным спектром в представлениях, где этот оператор диагонален. Таким образом, они играют роль базиса в диагональном представлении оператора.
- Важным применением дельта-функции является их участие в аппарате функций Грина линейных операторов. Для линейного оператора , действующего на обобщённые функции над многообразием , уравнение, определяющее функцию Грина с источником в точке имеет вид
- Особенно часто встречается применение этого аппарата к оператору Лапласа (электростатика, теплопроводность, диффузия, механическая теория упругости) и подобным ему операторам, таким как Оператор Д’Аламбера (акустика, электродинамика, квантовая теория поля, где функция Грина часто носит специальное название пропагатора).
- Для лапласиана в функцией Грина является функция , так что
- где — расстояние до начала координат. Этот факт используется для доказательства того, что выражение для скалярного потенциала
- удовлетворяет уравнению Пуассона:
См. также[править | править код]
Примечания[править | править код]
- ↑ Colombeau J. F. Elementary Introduction to New Generalized Functions. — Amsterdam: Elsevier Science Publishers B. V., 1985. — 281 с. — ISBN 978-0-444-87756-7.
- ↑ Егоров Ю. В. К теории обобщённых функций // УМН. — 1990. — Т. 45, вып. 5 (275). — С. 3—40.
Литература[править | править код]
- Дирак П. А. М. Основы квантовой механики / Пер. с англ. — М., 1932 (есть много переизданий).
- Кудрявцев Л. Д. Краткий курс математического анализа. — Том 2. — ISBN 5-9221-0185-4.
- Weisstein, Eric W. Delta Function (англ.) на сайте Wolfram MathWorld.
- Хермандер Л. Анализ линейных дифференциальных уравнений. — Том 1.
- Хермандер Л. Линейные дифференциальные операторы в частных производных.
- Гельфанд И. М., Шилов Г. Е. Обобщённые функции и действия над ними.
- Краснопевцев Е. А. Математические методы физики. Избранные вопросы.
Для улучшения этой статьи по математике желательно: |


















































![{\displaystyle \int _{I}f(x)\,dx=[(a_{1},\;a_{2},\;\ldots )],\;a_{i}=\int _{I}f_{i}(x)\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5436648292c10f1b49cc12960a1c54984da3becc)




























![{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\delta ^{[n]}(x-a)\,dx=-\int \limits _{-\infty }^{+\infty }{\frac {\partial f}{\partial x}}\delta ^{[n-1]}(x-a)\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39dcd65ddc90e7b98739f7ceaae2748aa7d0d7fe)
![{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\delta ^{[n]}(x-a)\,dx=\left.(-1)^{n}{\frac {\partial ^{n}f(x)}{\partial x^{n}}}\right|_{x=a}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2d832072d2bf85d5c3682d438d2901ea3a41724)