Ящик с усами

Не следует путать с японскими свечами.

График 1. Результаты эксперимента Майкельсона-Морли

График 2. Сравнение плотности распределения и ящика с усами

График 3. Функция вероятности нормального распределения

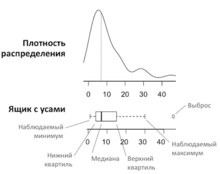
Ящик с усами, диаграмма размаха, усиковая диаграмма, коробчатая диаграмма, блочная диаграмма с ограничителями выбросов (англ. box-and-whiskers diagram, box-and-whiskers plot, box plot) — график, использующийся в описательной статистике, компактно изображающий одномерное распределение вероятностей.

Такой вид диаграммы в удобной форме показывает медиану (или, если нужно, среднее), нижний и верхний квантили, минимальное и максимальное значение выборки и выбросы. Несколько таких ящиков можно нарисовать бок о бок, чтобы визуально сравнивать одно распределение с другим; их можно располагать как горизонтально, так и вертикально. Расстояния между различными частями ящика позволяют определить степень разброса (дисперсии) и асимметрии данных и выявить выбросы.

Компактность представления информации

График «ящик с усами», или «ящичковая диаграмма», был разработан Джоном Тьюки в 1970-х годах. По сути, ящик с усами — это быстрый способ изучения одного или нескольких наборов данных в графическом виде. Этот график может показаться более примитивным, чем, например, гистограммы, но он имеет некоторые преимущества. Он занимает меньше места и поэтому особенно полезен для сравнения распределений между несколькими группами или наборами данных. Кроме того, ящик с усами в своей первоначальной форме прост для построения.

На графике 2 приведены два графических представления распределения одной и той же случайной величины. Сверху показана плотность распределения, а снизу ящик с усами. Видно, что ящик с усами более компактный и по нему легко можно оценить медианы, квантили, дисперсию и асимметрию в данных, а также выявить выбросы. Асимметрию данных можно увидеть не только по медиане, смещённой к какому-либо концу ящика, но и по разной длине усов, выходящих из ящика.

График «ящик с усами» очень прост для понимания и именно поэтому часто используется в различных публикациях для визуализации данных.

Построение

Границами ящика служат первый и третий квартили (25-й и 75-й процентили соответственно), линия в середине ящика — медиана (50-й процентиль). Концы усов — края статистически значимой выборки (без выбросов), и они могут определяться несколькими способами. Наиболее распространённые значения, определяющие длину «усов»:

• Минимальное и максимальное наблюдаемые значения данных по выборке (в этом случае выбросы отсутствуют);
• Разность первого квартиля и полутора межквартильных расстояний; сумма третьего квартиля и полутора межквартильных расстояний (в этом случае присутствуют выбросы). В общем виде эта формула имеет вид

 $X_{1}=Q_{1}-k(Q_{3}-Q_{1})$,  $X_{2}=Q_{3}+k(Q_{3}-Q_{1})$,

где $X_{1}$ — нижняя граница уса, $X_{2}$ — верхняя граница уса, $Q_{1}$ — первый квартиль, $Q_{3}$ — третий квартиль, $k$ — коэффициент, наиболее часто употребляемое значение которого равно 1,5. При этом длину верхнего уса ограничиваем максимальным значением по выборке, попадающим в верхнюю границу уса; длину нижнего уса ограничиваем минимальным значением по выборке, попадающим в длину нижнего уса. Поэтому длина верхнего и нижнего уса может не совпадать.

• Среднее арифметическое по выборке ± одно стандартное отклонение;
• 9-й и 91-й процентили;
• 2-й и 98-й процентили.

Данные, выходящие за границы усов (выбросы), отображаются на графике в виде точек, маленьких кружков или звёздочек.

Иногда на графике отмечают среднее арифметическое и его доверительный интервал («зарубка» в виде клина-выреза на ящике). Иногда зарубками обозначают доверительный интервал для медианы.

В связи с тем, что не существует единого общего согласия относительно того, как конкретно строить «ящик с усами», при виде такого графика необходимо искать информацию в сопроводительном тексте относительно того, по каким параметрам ящик с усами строился.

Модификации ящика с усами

График 4. Четыре ящика с усами с вырезами и без них и переменной шириной

Несмотря на свою простоту и удобство, первоначальная форма ящика с усами обладает и некоторыми недостатками. Один из таких существенных недостатков — отсутствие на графике информации о количестве наблюдений по выборке. Действительно, ящик с усами позволяет сравнить медианы, квартили, минимумы и максимумы по различным выборкам, но если мы захотим сделать вывод об общей медиане по всей совокупности выборок, то мы не сможем этого сделать, не прибегая к расчётам на исходных данных.

В 1978 году первоначальная форма ящика с усами была модифицирована МакГиллом, Ларсеном и Тьюки. Они предложили учитывать размер выборочной совокупности, рисуя ящики разной ширины (на графике 4 — variable width), а также изобразили на графике доверительный интервал для медиан в виде расходящихся клиньев-вырезов (на графике 4 — notched). Чем шире ящик — тем большее количество наблюдений в выборке, по которой строился этот ящик. Что касается доверительного интервала, то он представляет собой вырезы, расходящиеся от медианы на каждом из ящиков; в случае, если получившиеся вырезы разных ящиков не пересекаются, их медианы статистически значимо различаются.

Иная модификация получила название «histplot» (сокр. от «histogram plot», с англ. — «график-гистограмма»). Теперь на графике отображаются плотности распределения по трём точкам: медиане, первому и третьему квартилю. Соответственно, вместо прямоугольника, «ящик» теперь представляет собой две равнобедренные трапеции, имеющие смежное основание.

Дальнейшее изменение получило название «vaseplot» (с англ. — «график-ваза») из-за визуального сходства «ящика» с вазой. На данном графике производится отображение всех плотностей вероятностей от первого до третьего квартиля. Затемнённые области представляют собой доверительный интервал медианы.

Ссылки

• Поп-математика для взрослых детей
• Диаграмма размаха