Множество Делоне

Красные точки образуют часть $\varepsilon$-сети евклидовой плоскости, где $\varepsilon$ является радиусом больших жёлтых дисков. Синие диски половинного радиуса не пересекаются, а жёлтые покрывают всю плоскость, что удовлетворяет двум требованиям определения $\varepsilon$-сети.

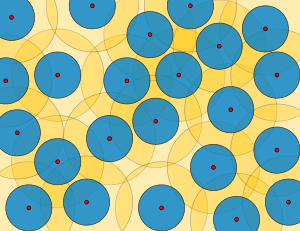
В теории метрических пространств, $\varepsilon$-сети, $\varepsilon$-упаковки, $\varepsilon$-покрытия, равномерно дискретные множества, относительно плотные множества и множества Делоне (названы именем советского математика Бориса Николаевича Делоне) являются тесно связанными определениями множеств точек, а радиус упаковки и радиус покрытия этих множеств определяют, насколько хорошо точки этих множеств разнесены. Множества Делоне имеют применение в теории кодирования, аппроксимационных алгоритмах и теории квазикристаллов.

Определения

Радиус упаковки подмножества X метрического пространства (M, d) - половина расстояния между ближайшими точками подмножества X. Если радиус упаковки равен r, то открытые шары радиуса r с центрами в точках X не пересекаются, а любой открытый шар с центром в точке из X и радиусом 2r не содержит других точек X. Радиус покрытия множества X есть инфимум чисел ''r'', таких что любая точка ''M'' находится не далее чем на расстоянии ''r'' по меньшей мере от одной точки. То есть это наименьший радиус, такой что объединение замкнутых шаров этого радиуса с центрами в множестве X равно пространству M. Множество X есть $\varepsilon$-упаковка, если радиус упаковки $\geqslant \varepsilon$/2 (эквивалентно, минимальное расстояние $\geqslant \varepsilon$), $\varepsilon$-покрытие есть множество X с радиусом покрытия $\leqslant \varepsilon$, а $\varepsilon$-сеть есть множество, являющееся одновременно и $\varepsilon$-упаковкой, и $\varepsilon$-покрытием. Множество называется однородно дискретным, если оно имеет ненулевой радиус упаковки и относительно плотным, если имеет конечный радиус покрытия. Множество Делоне есть множество, являющееся одновременно и однородно дискретным, и относительно плотным. Тогда любая $\varepsilon$-сеть является множеством Делоне, но обратное неверно.

Правильные системы и кристаллы

Множество Делоне называется правильной системой, если его группа симметрий G действует транзитивно на множестве X (то есть X есть G-орбита одной точки). Множество Делоне называется кристаллом, если X есть G-орбита некоторого конечного множества. Правильная система является важным частным случаем кристалла.

1. На плоскости любое множество Делоне, в котором все 4R-окрестности эквивалентны, есть правильная система.
2. В пространстве любой размерности значение 4R неулучшаемо
3. В 3D-пространстве любое множество Делоне, в котором все 10R-кластеры эквивалентны, есть правильная система.
4. В пространстве любой размерности имеется верхняя оценка для такого радиуса, что идентичность кластеров данного радиуса во множестве Делоне гарантирует его правильность.

Построение ε-сетей

Как определение с наибольшими ограничениями $\varepsilon$-сети построить не проще чем $\varepsilon$-упаковки, $\varepsilon$-покрытия и множества Делоне. Однако, если точки множества M являются вполне упорядоченным множеством, трансфинитная индукция показывает, что можно построить $\varepsilon$-сеть N, включая в N каждую точку, для которой инфимум расстояний до множества предшествующих точек в порядке по мешьшей мере $\varepsilon$. Для конечного множества точек в евклидовом пространстве ограниченной размерности каждую точку можно проверить за постоянное время путём отображения в решётку ячеек диаметра $\varepsilon$ и использования хеш-таблицы для проверки, какие соседние ячейки уже содержат точки N. Таким образом, $\varepsilon$-сеть может быть построена за линейное время.

Для более общих конечных или компактных метрических пространств, альтернативный алгоритм Теофило Гонсалеса, основанный на выборе наиболее удалённых точек, может быть использован для построения конечной $\varepsilon$-сети. Этот алгоритм начинает с пустой сети N и добавляет в N самую дальнюю от N точку из M, произвольно разрывая связи, и останавливается, когда все точки M находятся на расстоянии $\varepsilon$ от N. В пространствах ограниченной размерности удвоения алгоритм Гонсалеса можно реализовать со временем работы $O(n\log n)$ для множеств точек с полиномиальной зависимостью между самым большим и самым маленьким расстоянием, а также реализовать алгоритм приближённого решения задачи с тем же временем работы и произвольными множествами точек.

Приложения

Теория кодирования

Для $A_{q}(n,d)$ кода C (подмножество ${\mathcal {A}}_{q}^{n}$), радиус покрытия C – это наименьшее значение r, такое что любой элемент ${\mathcal {A}}_{q}^{n}$ содержится по меньшей мере в одном шаре радиуса r с центром в кодовом слове из C. Радиус упаковки C – это наибольшее значение s, такое что множество шаров радиуса s с центрами в C попарно не пересекаются. Из доказательства границы Хэмминга можно получить, что для $t\,=\,\left\lfloor {\frac {1}{2}}(d-1)\right\rfloor$ имеет место

$s\leqslant t\leqslant r$.

Поэтому, $s\leqslant r$ и если имеет место равенство, то $s=r=t$. Случай равенства означает, что граница Хэмминга достигнута.

В теории корректирующих кодов метрическое пространство, содержащее блочный код C, состоит из строк постоянной длины, скажем n, над алфавитом размера q (можно считать векторами) с расстояниями Хэмминга. Это пространство обозначается как ${\mathcal {A}}_{q}^{n}$. Радиус покрытия и радиус упаковки этого метрического пространства связан с возможностью кодов корректировать ошибки.

Алгоритмы приближения

Хар-Пелед и Рейчел описывают алгоритмическую парадигму, которую они называют «построение сети и обрезкой» для разработки аппроксимационных алгоритмов для геометрических задач оптимизации определённых типов, определённых на множествах точек в евклидовых пространствах. Алгоритм этого типа работает путём выполнения следующих шагов:

1. Выбираем случайную точку p из множества точек, находим ближайшего соседа q и полагаем $\varepsilon$ равным расстоянию между p и q.
2. Проверяем, является ли $\varepsilon$ (примерно) больше или меньше оптимального значения (используя технику, определяемую спецификой решаемой задачи оптимизации)
   • Если значение больше, удаляем из входных данных точки, ближайшие соседи которых находятся дальше, чем на $\varepsilon$
   • Если значение меньше, строим $\varepsilon$-сеть N и удаляем из входных данных точки, не принадлежащие N.

В обоих случаях ожидаемое число оставшихся точек уменьшается на постоянный множитель, так что время работы определяется шагом тестирования. Как они показали, такая парадигма может быть использована для построения быстрых аппроксимационных алгоритмов нахождения k-центра, нахождения пары точек со средним расстоянием и некоторых связанных задач.

Иерархическая система сетей, называемая деревом сетей, может быть использована в пространствах ограниченной размерности удвоения для построения вполне разделенных декомпозиционных пар, геометрических остовов и приближённого решения задачи о ближайших соседях .

Кристаллография

Для точек в евклидовом пространстве множество X является множеством Мейера, если оно относительно плотно и его разность Минковского $X-X$ равномерно дискретна. Эквивалентно, X является множеством Мейера, если и X и $X-X$ является множеством Делоне. Множества Мейера названы именем Ива Мейера, который ввёл их (с другим, но эквивалентным определением на основе гармонического анализа) в качестве математической модели для квазикристаллов. Они включают множества точек решёток, мозаики Пенроуза и суммы Минковского этих конечных множеств.

Ячейки Вороного симметричных множеств Делоне образуют заполняющие пространство многогранники, которые называются плезиоэдрами.

См. также

• Множество Данцера

Ссылки

• Delone set – Tilings Encyclopedia