Построение Витхоффа

Построения Витхоффа с тремя зеркалами, образующими прямоугольный треугольник.

Построение Витхоффа, или конструкция Витхоффа — метод построения однородных многогранников или мозаик на плоскости. Метод назван по имени математика В. А. Витхоффа. Часто метод построения Витхоффа называют калейдоскопным построением.

Построение

Построение основано на идее мозаик на сфере с использованием сферических треугольников — см. треугольники Шварца. Это построение использует отражения относительно сторон треугольника подобно калейдоскопу. Однако, в отличие от калейдоскопа, отражения не параллельны, а пересекаются в одной точке. Многократные отражения образуют несколько копий треугольника. Если углы сферического треугольника выбраны правильно, треугольники покрывают сферу мозаикой один или более раз.

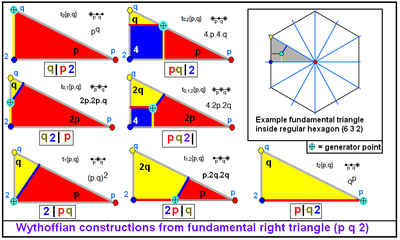
Если поместить точку в подходящее место внутри сферического треугольника, окружённого зеркалами, можно добиться, чтобы отражения этой точки дали однородный многогранник. Для сферического треугольника ABC имеются четыре позиции, которые дают однородный многогранник:

1. Точка расположена в вершине A. Она даёт многогранник с символом Витхоффа a|b c, где a равен π, делённому на угол треугольника в вершине A. Аналогично для b и c.
2. Точка расположена на отрезке AB в основании биссектрисы угла в вершине C. Она даёт многогранник с символом Витхоффа a b|c.
3. Точка расположена в инцентре треугольника ABC. Она даёт многогранник с символом Витхоффа a b c|.
4. Точка расположена таким образом, что при вращении её вокруг вершин треугольника на удвоенный угол при этих вершинах, она перемещается на одно и то же расстояние. Используются только чётные отражения. Многогранник имеет символ Витхоффа |a b c.

Процесс, в общем случае, применим и для получения правильных политопов в пространствах более высоких размерностей, включая 4-мерные однородные политопы.

Примеры

Шестиугольная призма строится как из семейства (6 2 2), так и из семейства (3 2 2).

Обрезанная квадратная мозаика строится с помощью двух различных позиций в семействе (4 4 2).

Невитхоффово построение

Однородные многогранники, которые нельзя построить с помощью зеркального построения Витхоффа, называются невитхоффовыми. Их, в общем случае, можно получить из витхоффовых построений либо альтернацией (удаление вершин через одну) или вставкой чередующихся рядов некоторых фигур. Оба типа таких фигур обладают вращательной симметрией. Иногда обрезки считаются витхоффовыми, даже если они могут быть получены путём альтернации обрезанных со всех сторон фигур.

Примеры

Шестиугольная антипризма строится с помощью альтернации двенадцатиугольной призмы.

Удлинённая треугольная мозаика строится путём чередования строк квадратной мозаики и треугольной мозаики.

Большой биромбоикосододекаэдр является единственным невитхоффовым однородным многогранником.

См. также

• Символ Витхоффа — символ для построения Витхоффа однородных многогранников и однородных мозаик.
• Диаграммы Коксетера — Дынкина — обобщённый символ для построения Витхоффа однородных многогранников и сот.

Ссылки

• Weisstein, Eric W. Wythoff Construction (англ.) на сайте Wolfram MathWorld.
• Olshevsky, George Wythoff construction at Glossary for Hyperspace
• Однородные многоугольники, полученные с помощью построения Витхоффа
• Описание построения Витхоффа
• «Jenn», программное обеспечение для просмотра (сферических) многоугольников и четырёхмерных политопов из их групп симметрии