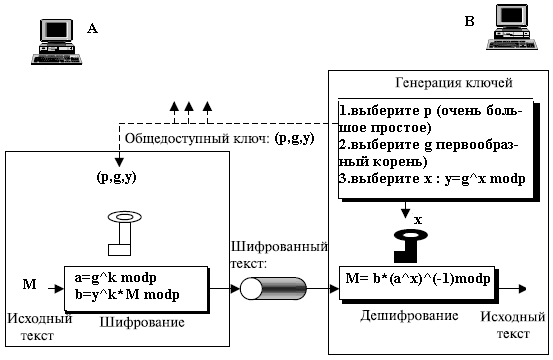
Схема Эль-Гамаля
Схема Эль-Гамаля (Elgamal) — криптосистема с открытым ключом, основанная на трудности вычисления дискретных логарифмов в конечном поле. Криптосистема включает в себя алгоритм шифрования и алгоритм цифровой подписи. Схема Эль-Гамаля лежит в основе бывших стандартов электронной цифровой подписи в США (DSA) и России (ГОСТ Р 34.10-94).
Схема была предложена Тахером Эль-Гамалем в 1985 году[1]. Эль-Гамаль разработал один из вариантов алгоритма Диффи-Хеллмана. Он усовершенствовал систему Диффи-Хеллмана и получил два алгоритма, которые использовались для шифрования и для обеспечения аутентификации. В отличие от RSA, алгоритм Эль-Гамаля не был запатентован и поэтому стал более дешёвой альтернативой, так как не требовалось оплаты взносов за лицензию. Считается, что алгоритм попадает под действие патента Диффи-Хеллмана.
Генерация ключей[править | править код]
- Генерируется случайное простое число .
- Выбирается целое число — первообразный корень .
- Выбирается случайное целое число такое, что .
- Вычисляется .
- Открытым ключом является , закрытым ключом — число .
Работа в режиме шифрования[править | править код]
Шифросистема Эль-Гамаля является фактически одним из способов выработки открытых ключей Диффи — Хеллмана.[источник не указан 879 дней] Шифрование по схеме Эль-Гамаля не следует путать с алгоритмом цифровой подписи по схеме Эль-Гамаля.
Шифрование[править | править код]
Сообщение должно быть меньше числа . Сообщение шифруется следующим образом:
- Выбирается сессионный ключ — случайное целое число, такое, что .
- Вычисляются числа и .
- Пара чисел является шифротекстом.
Нетрудно заметить, что длина шифротекста в схеме Эль-Гамаля вдвое больше исходного сообщения .
Расшифрование[править | править код]
Зная закрытый ключ , исходное сообщение можно вычислить из шифротекста по формуле:
При этом нетрудно проверить, что
и поэтому
- .
Для практических вычислений больше подходит следующая формула:
Схема шифрования[править | править код]
Пример[править | править код]
- Шифрование
- Допустим, что нужно зашифровать сообщение .
- Произведем генерацию ключей:
- Пусть . Выберем — случайное целое число такое, что .
- Вычислим .
- Итак, открытым ключом является тройка ,а закрытым ключом — число .
- Выбираем случайное целое число такое, что 1 < k < (p − 1). Пусть .
- Вычисляем число .
- Вычисляем число .
- Полученная пара является шифротекстом.
- Расшифрование
- Необходимо получить сообщение по известному шифротексту и закрытому ключу .
- Вычисляем M по формуле:
- Получили исходное сообщение .
Так как в схему Эль-Гамаля вводится случайная величина ,то шифр Эль-Гамаля можно назвать шифром многозначной замены. Из-за случайности выбора числа такую схему ещё называют схемой вероятностного шифрования. Вероятностный характер шифрования является преимуществом для схемы Эль-Гамаля, так как у схем вероятностного шифрования наблюдается большая стойкость по сравнению со схемами с определённым процессом шифрования. Недостатком схемы шифрования Эль-Гамаля является удвоение длины зашифрованного текста по сравнению с начальным текстом. Для схемы вероятностного шифрования само сообщение и ключ не определяют шифротекст однозначно. В схеме Эль-Гамаля необходимо использовать различные значения случайной величины для шифровки различных сообщений и . Если использовать одинаковые , то для соответствующих шифротекстов и выполняется соотношение . Из этого выражения можно легко вычислить , если известно .
Работа в режиме подписи[править | править код]
Цифровая подпись служит для того чтобы можно было установить изменения данных и чтобы установить подлинность подписавшейся стороны. Получатель подписанного сообщения может использовать цифровую подпись для доказательства третьей стороне того, что подпись действительно сделана отправляющей стороной. При работе в режиме подписи предполагается наличие фиксированной хеш-функции , значения которой лежат в интервале .
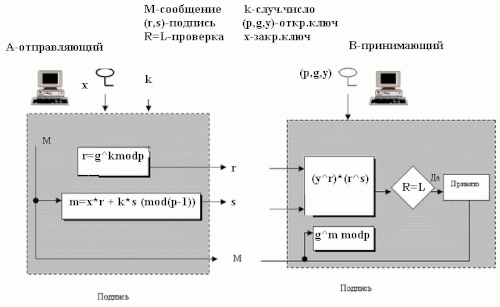
Подпись сообщений[править | править код]
Для подписи сообщения выполняются следующие операции:
- Вычисляется дайджест сообщения : (Хеш функция может быть любая).
- Выбирается случайное число взаимно простое с и вычисляется
- Вычисляется число , где это мультипликативное обратное по модулю , которое можно найти, например, с помощью расширенного алгоритма Евклида.
- Подписью сообщения является пара .
Проверка подписи[править | править код]
Зная открытый ключ , подпись сообщения проверяется следующим образом:
- Проверяется выполнимость условий: и .
- Если хотя бы одно из них не выполняется, то подпись считается неверной.
- Вычисляется дайджест
- Подпись считается верной, если выполняется сравнение:
Корректность проверки[править | править код]
Рассматриваемый алгоритм корректен в том смысле, что подпись, вычисленная по указанным выше правилам, будет принята при её проверке.
Преобразуя определение , имеем
Далее, из Малой теоремы Ферма следует, что
Пример[править | править код]
- Подпись сообщения.
- Допустим, что нужно подписать сообщение .
- Произведем генерацию ключей:
- Пусть переменные, которые известны некоторому сообществу.
- Секретный ключ — случайное целое число такое, что .
- Вычисляем открытый ключ : .
- Итак, открытым ключом является тройка .
- Теперь вычисляем хеш-функцию: .
- Выберем случайное целое число такое, что выполняется условие . Пусть .
- Вычисляем .
- Находим . Такое число существует, так как НОД. Его можно найти с помощью расширенного алгоритма Евклида. Получим
- Находим число . Получим , так как
- Итак, мы подписали сообщение: .
- Проверка подлинности полученного сообщения.
- Вычисляем хеш-функцию: .
- Проверяем сравнение .
- Вычислим левую часть по модулю 23: .
- Вычислим правую часть по модулю 23: .
- Так как правая и левая части равны, то это означает что подпись верна.
- Главным преимуществом схемы цифровой подписи Эль-Гамаля является возможность вырабатывать цифровые подписи для большого числа сообщений с использованием только одного секретного ключа. Чтобы злоумышленнику подделать подпись, ему нужно решить сложные математические задачи с нахождением логарифма в поле . Следует сделать несколько комментариев:
- Случайное число должно сразу после вычисления подписи уничтожаться, так как если злоумышленник знает случайное число и саму подпись, то он легко может найти секретный ключ по формуле: и полностью подделать подпись.
Число должно быть случайным и не должно дублироваться для различных подписей, полученных при одинаковом значении секретного ключа.
- Использование свертки объясняется тем, что это защищает подпись от перебора сообщений по известным злоумышленнику значениям подписи. Пример: если выбрать случайные числа ,удовлетворяющие условиям , НОД(j, p-1)=1 и предположить что
то легко удостовериться в том, что пара является верной цифровой подписью для сообщения .
- Цифровая подпись Эль-Гамаля стала примером построения других подписей, схожих по своим свойствам. В их основе лежит выполнение сравнения: , в котором тройка принимает значения одной из перестановок ±r, ±s и ±m при каком-то выборе знаков. Например, исходная схема Эль-Гамаля получается при , , .На таком принципе построения подписи сделаны стандарты цифровой подписи США и России. В американском стандарте DSS (Digital Signature Standard), используется значения , , , а в Российском стандарте: , , .
- Ещё одним из преимуществ является возможность уменьшения длины подписи с помощью замены пары чисел на пару чисел ), где является каким-то простым делителем числа . При этом сравнение для проверки подписи по модулю нужно заменить на новое сравнение по модулю : . Так сделано в американском стандарте DSS (Digital Signature Standard).
Криптостойкость и особенности[править | править код]
В настоящее время криптосистемы с открытым ключом считаются наиболее перспективными. К ним относится и схема Эль-Гамаля, криптостойкость которой основана на вычислительной сложности проблемы дискретного логарифмирования, где по известным p, g и y требуется вычислить x, удовлетворяющий сравнению:
ГОСТ Р34.10-1994, принятый в 1994 году в Российской Федерации, регламентировавший процедуры формирования и проверки электронной цифровой подписи, был основан на схеме Эль-Гамаля. С 2001 года используется новый ГОСТ Р 34.10-2001, использующий арифметику эллиптических кривых, определённых над простыми полями Галуа. Существует большое количество алгоритмов, основанных на схеме Эль-Гамаля: это алгоритмы DSA, ECDSA, KCDSA, схема Шнорра.
Сравнение некоторых алгоритмов:
| Алгоритм | Ключ | Назначение | Криптостойкость, MIPS | Примечания |
| RSA | До 4096 бит | Шифрование и подпись | 2,7•1028 для ключа 1300 бит | Основан на трудности задачи факторизации больших чисел; один из первых асимметричных алгоритмов. Включен во многие стандарты |
| ElGamal | До 4096 бит | Шифрование и подпись | При одинаковой длине ключа криптостойкость равная RSA, т.е. 2,7•1028 для ключа 1300 бит | Основан на трудной задаче вычисления дискретных логарифмов в конечном поле; позволяет быстро генерировать ключи без снижения стойкости. Используется в алгоритме цифровой подписи DSA-стандарта DSS |
| DSA | До 1024 бит | Только подпись | Основан на трудности задачи дискретного логарифмирования в конечном поле; принят в качестве гос. стандарта США; применяется для секретных и несекретных коммуникаций; разработчиком является АНБ. | |
| ECDSA | До 4096 бит | Шифрование и подпись | Криптостойкость и скорость работы выше, чем у RSA | Современное направление. Разрабатывается многими ведущими математиками |
Примечания[править | править код]
Литература[править | править код]
- Elgamal T. A Public-Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms, A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms (англ.) // IEEE Transactions on Information Theory / F. Kschischang — IEEE, 1985. — P. 10—18. — ISSN 0018-9448; 1557-9654 — doi:10.1109/TIT.1985.1057074; doi:10.1007/3-540-39568-7_2
- Алфёров А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы криптографии.[уточнить]
- Б. А. Фороузан. Схема цифровой подписи Эль-Гамаля // Управление ключами шифрования и безопасность сети / Пер. А. Н. Берлин. — Курс лекций.
- Menezes A. J., Oorschot P. v., Vanstone S. A. 11.5.2 The ElGamal signature scheme // Handbook of Applied Cryptography (англ.) — CRC Press, 1996. — 816 p. — (Discrete Mathematics and Its Applications) — ISBN 978-0-8493-8523-0