Феномен Рунге

Интерполяция функции Рунге многочленами пятой (слева) и десятой степени (справа)

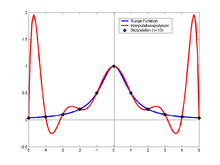
Феномен Рунге — эффект нежелательных колебаний, возникающий при интерполяции полиномами высоких степеней. Был открыт Карлом Рунге при изучении ошибок полиномиальной интерполяции для приближения некоторых функций.

Рассмотрим функцию $f(x)={\frac {1}{1+25x^{2}}}.$ Если интерполировать её по $n$ равноотстоящим узлам $x_{i}$ между $-5$ и $5$, то есть по узлам

$x_{i}=-5+(i-1){\frac {10}{n}},\quad i=1,\dots ,n+1$

с помощью полинома $P_{n}(x)$ степени не больше $n$, то полученный интерполянт будет осциллировать ближе к концам интервала. С возрастанием степени полинома погрешность интерполяции стремится к бесконечности:

$\lim _{n\rightarrow \infty }\left(\max _{-5\leq x\leq 5}|f(x)-P_{n}(x)|\right)=\infty .$

Такой эффект роста отклонения при росте степени многочлена зависит как от выбираемой последовательности узлов, так и от интерполируемой функции. Именно, для любой последовательности узлов можно подобрать такую непрерывную функцию, что ошибка её интерполяции по этим узлам будет неограниченно расти. С другой стороны, согласно аппроксимационной теореме Вейерштрасса, для любой непрерывной функции на отрезке можно подобрать последовательность полиномов, равномерно сходящихся к этой функции на отрезке. Это теоретически позволяет подобрать для заданной функции последовательность узлов, гарантирующую отсутствие феномена Рунге.

Компромиссом можно считать узлы Чебышёва, погрешность интерполяции по которым равномерно убывает для любой абсолютно непрерывной функции.