Задача об иголке

Задача об иголке состоит в определении минимальной площади фигуры на плоскости, в которой единичный отрезок, «иглу», можно развернуть на 180 градусов, вернув его в исходное положение с обращённой ориентацией. Такое возможно проделать в круге радиуса 1/2. Другой пример — фигура, ограниченная дельтоидой, — показан на картинке, он имеет меньшую площадь.
Оказывается, что можно построить фигуру с произвольно малой площадью.
История
[править | править код]Этот вопрос рассматривал Какея[яп.]. Он доказал, что для выпуклых областей минимальная площадь достигается для равностороннего треугольника с высотой 1. Его площадь равна [1].
Возможно, Какея также выдвинул гипотезу, что фигура, ограниченная дельтоидой, как на рисунке, имеет наименьшую площадь. Это утверждение было опровергнуто Безиковичем.
Множество Безиковича
[править | править код]А. С. Безикович построил компактное множество нулевой меры, содержащее единичный отрезок в любом направлении.
Отсюда легко следует, что иглу можно развернуть в фигуре произвольно малой площади. Действительно, легко видеть, что единичный круг можно разбить на секторы и одними параллельными переносами поместить в произвольно малую окрестность множества .
Заметим, что единичный отрезок можно передвинуть на параллельную прямую в фигуре произвольно малой площади. Поэтому, повернув отрезок в одном секторе, его можно перетащить в следующий, пройдя по множеству произвольно малой площади; повторив эту операцию несколько раз, получим требуемый разворот.
Вариации и обобщения
[править | править код]- В конструкции Безиковича при стремлении площади фигуры к нулю её диаметр стремится к бесконечности. В 1941 году Х. Дж. Ван Альфен показал[2], что иглу можно развернуть в фигуре сколь угодно малой площади, которая находится внутри круга с радиусом 2 + ε (для произвольного ε > 0).
- Существуют односвязные подходящие (в которых можно развернуть иглу) множества с площадью меньшей, чем у фигуры, ограниченной дельтоидой.
- Такие примеры были найдены в 1965 году. Мелвин Блум и И. Ю. Шенберг показали, что их площадь можно сделать произвольно близкой к .
- В 1971 году Каннингем показал[3], что для любого ε > 0 существует подходящая односвязная фигура с площадью менее , содержащаяся в круге радиуса 1.
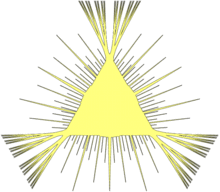
- Определим множество Безиковича[англ.]* в Rn как множество нулевой меры, содержащее единичный отрезок в любом направлении (такое множество также называется множеством Какея, или множеством Какейя). Так называемая гипотеза Какея утверждает, что множества Безиковича имеют размерность n (по Хаусдорфу и по Минковскому), то есть равна размерности объемлющего пространства.
- Определим (n, k)-множество Безиковича как компактное множество в Rn нулевой меры, содержащее в каждом k-мерном направлении k-мерный единичный диск.
- Гипотеза про (n, k)-множества Безиковича: (n, k)-множеств Безиковича не существует при k > 1.
- В 1997[10] и 1999[11] году Вольфф доказал, что множества, содержащие сферу любого радиуса, должны иметь полную размерность, то есть размерность объемлющего пространства.
- Элиас Штайн доказал[12], что любое множество, содержащее сферу вокруг каждой точки, должно иметь положительную меру при n ≥ 3, и Марстранд доказал[13] то же для случая n = 2.
- В 1999 году Вольфф сформулировал аналог задачи об игле для конечных полей. Пусть F — конечное поле. Множество K ⊆ Fn называется множеством Безиковича, если для каждого вектора y∈Fn существует такой x∈Fn, что K содержит все вектора вида {x + ty : t ∈ F}.
- Задача об игле в пространстве над конечным полем: Число элементов в K не меньше cn|F|n, где cn>0 — константа, которая зависит только от n.
- Двир[14][15] доказал эту гипотезу для cn = 1/n!, используя следующий аргумент. Двир отметил, что любой многочлен с n переменными степени менее чем |F|, который равен нулю на множестве Безиковича, должен быть тождественно равен нулю. С другой стороны, многочлены с n переменными степени менее чем |F| образуют векторное пространство размерности
- Следовательно, существует хотя бы один нетривиальный многочлен степени меньше, чем |F|, который равен нулю на произвольном множестве с меньшим числом точек. Отсюда множество Безиковича должно иметь хотя бы |F|n/n! точек. Двир написал обзорную статью об этой задаче.[14]
Приложения
[править | править код]- В 1971 году Фефферман использовал[16] построение множества Безиковича, чтобы показать, что в размерности большей, чем 1, усеченные интегралы Фурье, взятые по шарам с центром в начале координат с радиусами, стремящимися к бесконечности, могут не сходиться по норме Lp при р ≠ 2 (в отличие от одномерного случая, где такие усеченные интегралы сходятся).
См. также
[править | править код]Примечания
[править | править код]- ↑ Pal, Julius. Ueber ein elementares variationsproblem // Kongelige Danske Videnskabernes Selskab Math.-Fys. Medd.. — 1920. — Т. 2. — С. 1–35.
- ↑ Alphen, H. J. Uitbreiding van een stelling von Besicovitch // Mathematica Zutphen B. — 1942. — Т. 10. — С. 144–157.
- ↑ Cunningham, F. The Kakeya problem for simply connected and for star-shaped sets : [арх. 14 июля 2010] // American Mathematical Monthly. — 1971. — Т. 78, вып. 2. — С. 114–129. — doi:10.2307/2317619.
- ↑ Davies, Roy. Some remarks on the Kakeya problem // Proc. Cambridge Philos. Soc.. — 1971. — Т. 69, вып. 3. — С. 417–421. — doi:10.1017/S0305004100046867.
- ↑ Wolff, Thomas. An improved bound for Kakeya type maximal functions // Rev. Mat. Iberoamericana. — 1995. — Т. 11. — С. 651–674. — doi:10.4171/rmi/188.
- ↑ Katz, Nets Hawk; Tao, Terence. New bounds for Kakeya problems // J. Anal. Math.. — 2002. — Т. 87. — С. 231–263. — doi:10.1007/BF02868476.
- ↑ Marstrand, J. M. Packing Planes in R3 // Mathematika. — 1979. — Т. 26, вып. 2. — С. 180–183. — doi:10.1112/S0025579300009748.
- ↑ Falconer, K. J. Continuity properties of k-plane integrals and Besicovitch sets // Math. Proc. Cambridge Philos. Soc.. — 1980. — Т. 87, вып. 2. — С. 221–226. — doi:10.1017/S0305004100056681.
- ↑ Bourgain, Jean. Besicovitch type maximal operators and applications to Fourier analysis // Geom. Funct. Anal.. — 1997. — Т. 1, вып. 2. — С. 147–187. — doi:10.1007/BF01896376.
- ↑ Wolff, Thomas. A Kakeya problem for circles // American Journal of Mathematics. — 1997. — Т. 119, вып. 5. — С. 985–1026. — doi:10.1353/ajm.1997.0034.
- ↑ Wolff, Thomas (1999).
- ↑ Stein, Elias. Maximal functions: Spherical means // PNAS. — 1976. — Т. 73, вып. 7. — С. 2174–2175. — doi:10.1073/pnas.73.7.2174. PMC 430482
- ↑ Marstrand, J. M. Packing circles in the plane // Proceedings of the London Mathematical Society. — 1987. — Т. 55. — С. 37–58. — doi:10.1112/plms/s3-55.1.37.
- ↑ 1 2 Dvir, Zeev (2009).
- ↑ Dvir’s proof of the finite field Kakeya conjecture Архивная копия от 3 мая 2016 на Wayback Machine // Terence Tao (2008-03-24).
- ↑ Fefferman, Charles. The multiplier problem for the ball // Annals of Mathematics. — 1971. — Т. 94, вып. 2. — С. 330–336. — doi:10.2307/1970864.
Литература
[править | править код]- Яглом И. М., Болтянский В. Г. Выпуклые фигуры. — М.—Л.: ГТТИ, 1951. — 343 с. — (Библиотека математического кружка, вып. 4).
- Besicovitch, Abram (1963). «The Kakeya Problem». American Mathematical Monthly 70 (7): 697—706. doi:10.2307/2312249. JSTOR 2312249. MR 0157266.
- Dvir, Zeev (2009). «On the size of Kakeya sets in finite fields». Journal of the American Mathematical Society 22 (4): 1093—1097. arXiv: 0803.2336. doi:10.1090/S0894-0347-08-00607-3. MR 2525780.
- Falconer, Kenneth J. (1985). The Geometry of Fractal Sets. Cambridge Tracts in Mathematics 85. Cambridge: Cambridge University Press. ISBN 0-521-25694-1. MR 0867284.
- Kakeya, Soichi (1917). «Some problems on maximum and minimum regarding ovals». Tohoku science reports 6: 71-88.
- Katz, Nets Hawk; Łaba, Izabella; Tao, Terence (2000). «An improved bound on the Minkowski dimension of Besicovitch sets in » (PDF). Annals of Mathematics 152 (2): 383—446. doi:10.2307/2661389. JSTOR 2661389. MR 1804528.
- Wolff, Thomas (1999). «Recent work connected with the Kakeya problem». In Rossi, Hugo. Prospects in Mathematics: Invited Talks on the Occasion of the 250th Anniversary of Princeton University. Providence, RI: American Mathematical Society. pp. 129—162. ISBN 978-0-8218-0975-4. MR 1660476.
- Wolff, Thomas (2003). Łaba, Izabella; Shubin, Carol, eds. Lectures on Harmonic Analysis. University Lecture Series 29. With a foreword by Charles Fefferman and preface by Izabella Łaba. Providence, RI: American Mathematical Society. doi:10.1090/ulect/029. ISBN 0-8218-3449-5. MR 2003254.
Внешние ссылки
[править | править код]- The Kakeya problem, and connections to harmonic analysis at University of British Columbia.
- Besicovitch at UCLA
- Kakeya needle problem at mathworld
- An Introduction to Besicovitch-Kakeya Sets






