Проецирование в выпуклые множества

Проецирование в выпуклые множества (англ. projections onto convex sets, POCS), которое иногда упоминается как метод попеременного проецирования, является методом поиска точки в пересечении двух замкнутых выпуклых множеств. Это очень простой алгоритм и был переоткрыт много раз. Простой случай, когда множествами являются аффинные пространства, проанализировал Джон фон Нейман. Случай аффинных пространств является частным, поскольку итерации сходятся не просто к точке в пересечении (в предположении, что пересечение не пустое), а к ортогональной проекции (исходной) точки на пересечение множеств. Для случая общих замкнутых выпуклых множеств предельная точка не обязательно будет проекцией. Классическая работа для случая двух замкнутых выпуклых множеств показывает, что скорость сходимости итераций линейна. Имеются расширения, в которых рассматриваются случаи более одного множества, или когда множества не выпуклы, или варианты, дающие более быструю сходимость. При анализе POCS и связанных методов пытаются показать, что алгоритм сходится (и если тaк, пытаются найти скорость сходимости), и выяснить, сходится ли метод к проекции исходной точки. Ответы, в основном, известны для простых случаев, но эта область активно исследуется в направлении обобщений. Есть два варианта алгоритма, таких как алгоритм Дикстры. См. ссылки в разделе «Литература для дальнейшего чтения» с обзором вариантов, обобщений и приложений метода POCS. Хорошее изложение истории метода можно найти в разделе III книги Комбета.

Алгоритм

Пример двух окружностей

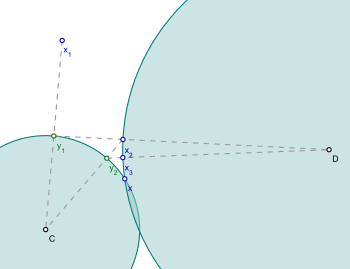
Алгоритм POCS решает следующую задачу:

найти $\;x\in \mathbb {R} ^{n}\quad$, такой, что $\;x\in C\cap D$

где C и D два замкнутых выпуклых множества.

Чтобы использовать алгоритм POCS, нужно знать, как проецировать в множества C и D по отдельности. Алгоритм начинается с произвольного значения $x_{0}$ и генерирует последовательность

$x_{k+1}={\mathcal {P}}_{C}\left({\mathcal {P}}_{D}(x_{k})\right).$

Простота алгоритма объясняет его популярность. Если пересечение множеств C и D не пусто, то последовательность, порождённая алгоритмом, будет сходиться к некоторой точке в их пересечении.

В отличие от алгоритма проектирования Дикстры, решение не обязательно окажется проекцией в пересечение множеств C и D.

Связанные алгоритмы

Пример варианта усреднённого проецирования

Метод усреднённого проецирования аналогичен. Для случая двух замкнутых выпуклых множеств C и D он работает по формуле

$x_{k+1}={\frac {1}{2}}({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(x_{k}))$

Давно известно, что он сходится глобально. Более того, метод просто обобщить на более чем два множества. Некоторые результаты сходимости для этого случая можно найти в статье Льюиса, Люка и Малика.

Метод усреднённого проецирования можно переформулировать как метод поочерёдного проецирования с помощью стандартного приёма. Рассмотрим множество

$E=\{(x,y):x\in C,\;y\in D\}$,

которое определено в произведении пространств $\mathbb {R} ^{n}\times \mathbb {R} ^{n}$. Определим теперь другое множество, также в произведении пространств:

$F=\{(x,y):x\in \mathbb {R} ^{n},\,y\in \mathbb {R} ^{n},\;x=y\}.$

Тогда нахождение $C\cap D$ эквивалентно нахождению $E\cap F$.

Чтобы найти точку в $E\cap F$, используем метод поочерёдного проецирования. Проекция вектора $(x,y)$ в множество F задаётся выражением $(x+y,x+y)/2$, следовательно,

$(x_{k+1},y_{k+1})={\mathcal {P}}_{F}({\mathcal {P}}_{E}((x_{k},y_{k})))={\mathcal {P}}_{F}(({\mathcal {P}}_{C}x_{k},{\mathcal {P}}_{D}y_{k}))={\frac {1}{2}}({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(y_{k}),({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(y_{k})).$

Поскольку $x_{k+1}=y_{k+1}$, в предположении, что $x_{0}=y_{0}$, будем иметь $x_{j}=y_{j}$ для всех $j\geqslant 0$, а следовательно, мы можем упростить итерацию до $x_{k+1}={\frac {1}{2}}({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(x_{k}))$.

Литература для дальнейшего чтения

• René Escalante, Marcos Raydan. Alternating Projection Methods. — SIAM, 2011.