Простой многоугольник

Простой многоугольник — это фигура, состоящая из непересекающихся отрезков («сторон»), соединённых попарно с образованием замкнутого пути. Если стороны пересекаются, многоугольник не является простым. Часто слово «простой» опускается из вышеприведённого определения.
Данное выше определение обеспечивает следующие свойства фигуры:
- Многоугольник окружает область (называемую внутренностью), которая всегда имеет измеримую площадь.
- Отрезки, образующие многоугольник (называемые сторонами, реже рёбрами), пересекаются только в их конечных точках, которые называются вершинами (или, менее формально, «углами»).
- В каждой вершине сходятся в точности две стороны.
- Число сторон всегда равно числу вершин.
Обычно требуется, чтобы две стороны, сходящиеся в вершине, не образовывали развёрнутый (180°) угол. В противном случае лежащие на одной прямой стороны считаются частью одной стороны.
Математики обычно используют термин «многоугольник» только для фигур, образованных отрезками, не включая внутреннюю область. Однако некоторые используют термин «многоугольник» для обозначения плоской фигуры ограниченной замкнутым путём, состоящим из конечной последовательности отрезков (то есть замкнутой ломаной). В зависимости от используемого определения граница может быть или не быть частью многоугольника[1].
Простые многоугольники называются также жордановыми многоугольниками, поскольку может быть использована теорема Жордана для доказательства, что такие многоугольники разбивают плоскость на две области, внутри и снаружи. Многоугольник на плоскости является простым тогда и только тогда, когда он топологически эквивалентнен окружности. Его внутренность топологически эквавалентна кругу.
Слабо простой многоугольник[править | править код]
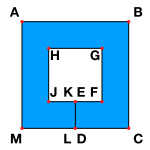
Если набор непересекающихся отрезков образует границу области на плоскости, топологически эквивалентную кругу, то эта граница называется слабо простым многоугольником[2]. На рисунке слева ABCDEFGHJKLM является слабо простым многоугольником согласно определению. Синим цветом отражена область, для которой слабо простой многоугольник является границей. Этот тип слабо простых многоугольников может возникнуть в компьютерной графике и в системах CAD в качестве компьютерного представления многоугольных областей с полостями — для каждой полости создаётся «разрез» для соединения с внешней границей. Согласно рисунку ABCM является внешней границей плоской области с полостью FGHJ. Разрез ED соединяет полость с внешним контуром и проходится дважды в представлении слабо простого многоугольника.
Альтернативное и более общее определение слабых простых многоугольников — предел последовательности простых многоугольников одного и того же комбинаторного типа, которые сходятся по расстоянию Фреше[3]. Это формализует идею, что элементам многоугольника разрешено касание, но не пересечение. Однако этот тип слабо простых многоугольников не обязательно образует границу области, так как «внутренность» может быть пустой. Например, на рисунке цепочке ABCBA является слабо простым многоугольником — его можно рассматривать как предел «выжимания» многоугольника ABCFGHA.
Вычислительные задачи[править | править код]
В вычислительной геометрии некоторые важные вычислительные задачи используют вход в виде простого многоугольника. В каждой этой задаче различие между внутренностью и внешностью является ключевым моментом[4]
- Задача о принадлежности точки многоугольнику требует определить, находится ли точка q во внутренней области многоугольника P.
- Простые формулы известны для вычисления площади многоугольника, то есть внутренней области.
- Разбиение многоугольника — это множество элементарных единиц (например, квадратов), которые не пересекаются и объединение которых образует многоугольник. Задача разбиения многоугольника заключается в нахождении разбиения, минимального в некотором смысле. Например, разбиение с минимальным числом единиц или с минимальной суммарной длиной сторон.
- Специальным случаем разделения многоугольника является задача о триангуляции многоугольника — разбиение простого многоугольника на треугольники. Хотя выпуклые многоугольники легко разбить на треугольники, триангуляция простых многоугольников общего вида является более сложной задачей, поскольку нужно избегать добавления рёбер, пересекающихся вне многоугольника. Тем не менее, Бернхард Чазелле в 1991 показал, что любой простой многоугольник с n вершинами можно разбить на треугольники за оптимальное время Θ(n). Тот же алгоритм может быть использован для определения, образует ли замкнутая ломаная простой многоугольник.
- Булевские операции над многоугольниками[англ.] — различные булевские операции на множестве точек, определённых внутренними областями многоугольников.
- Выпуклая оболочка простого многоугольника может быть вычислена более эффективно, чем выпуклая оболочка для других видов входных данных, таких как множество точек.
- Диаграмма Вороного простого многоугольника
- Срединная ось/топологический скелет/прямолинейный скелет простого многоугольника
- Параллельная кривая простого многоугольника
- Сумма Минковского для простых многоугольников
См. также[править | править код]
Примечания[править | править код]
- ↑ Grünbaum, 2003.
- ↑ Dumitrescu, Tóth, 2007, с. 177.
- ↑ Chang, Erickson, Xu, 2015, с. 1655–1670.
- ↑ comp.graphics.algorithms FAQ Архивная копия от 13 февраля 2011 на Wayback Machine со списком решений математических задач с 2D и 3D многоугольниками.
Литература[править | править код]
- Branko Grünbaum. Convex polytopes / Volker Kaibel, Victor Klee, Günter M. Ziegler. — 2nd. — New York, London: Springer-Verlag, 2003. — ISBN 0-387-00424-6.
- Adrian Dumitrescu, Csaba D. Tóth. STACS 2007: 24th Annual Symposium on Theoretical Aspects of Computer Science, Aachen, Germany, February 22-24, 2007, Proceedings / Wolfgang Thomas, Pascal Weil. — illustrated. — Springer, 2007. — ISBN 3540709177.
- Hsien-Chih Chang, Jeff Erickson, Chao Xu. Proceedings of the Twenty-Sixth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA'15). — 2015.
Ссылки[править | править код]
- Weisstein, Eric W. Simple polygon (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи желательно:
|