Сочетание

В комбинаторике сочетанием из $n$ по $k$ называется набор из $k$ элементов, выбранных из $n$-элементного множества, в котором не учитывается порядок элементов.

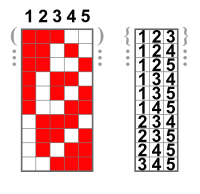
Соответственно, сочетания, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми — этим сочетания отличаются от размещений. Так, например, 3-элементные сочетания 2 и 3 ((нестрогие) подмножества, для которых $k=3$) из 6-элементного множества 1 ($n=6$) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов 1.

В общем случае число всех возможных $k$-элементных подмножеств $n$-элементного множества стоит на пересечении $k$-й диагонали и $n$-й строки треугольника Паскаля.

3х элементные подмножества 5 элементного множества

Число сочетаний

Основная статья: Биномиальный коэффициент

Число сочетаний из $n$ по $k$ равно биномиальному коэффициенту

${n \choose k}=C_{n}^{k}={\frac {n!}{k!\left(n-k\right)!}}.$

При фиксированном $n$ производящей функцией последовательности чисел сочетаний ${\tbinom {n}{0}}$, ${\tbinom {n}{1}}$, ${\tbinom {n}{2}}$, … является

$\sum _{k=0}^{n}{\binom {n}{k}}x^{k}=(1+x)^{n}.$

Двумерной производящей функцией чисел сочетаний является

$\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\binom {n}{k}}x^{k}y^{n}=\sum _{n=0}^{\infty }(1+x)^{n}y^{n}={\frac {1}{1-y-xy}}.$

Сочетания с повторениями

Сочетанием с повторениями из $n$ по $k$ называется такой $k$-элементный набор из $n$-элементного множества, в котором каждый элемент может участвовать несколько раз, но в котором порядок не учитывается (мультимножество). В частности, число монотонных неубывающих функций из множества $\{1,2,\dots ,k\}$ в множество $\{1,2,\dots ,n\}$ равно числу сочетаний с повторениями из $n$ по $k$.

Число сочетаний с повторениями из $n$ по $k$ равно биномиальному коэффициенту

${\overline {C_{n}^{k}}}=C_{(n)}^{k}=\left(\!\!{\binom {n}{k}}\!\!\right)={\binom {n+k-1}{n-1}}={\binom {n+k-1}{k}}=(-1)^{k}{\binom {-n}{k}}={\frac {(n+k-1)!}{k!\cdot (n-1)!}}.$

Доказательство

Пусть имеется $n$ типов объектов, причём объекты одного типа неотличимы. Пусть имеется неограниченное (или достаточно большое, во всяком случае, не меньше $k$) число объектов каждого типа. Из этого ассортимента выберем $k$ объектов; в выборке могут встречаться объекты одного типа, порядок выбора не имеет значения. Обозначим через $x_{j}$ число выбранных объектов $j$-го типа, $x_{j}\geq 0$, $j=1,2,\dots ,n$. Тогда $x_{1}+x_{2}+\dots +x_{n}=k$. Но число решений этого уравнения легко подсчитывается с помощью «шаров и перегородок»: каждое решение соответствует расстановке в ряд $k$ шаров и $n-1$ перегородок так, чтобы между $(j-1)$-й и $j$-й перегородками находилось ровно $x_{j}$ шаров. Но таких расстановок в точности ${\tbinom {n+k-1}{k}}$, что и требовалось доказать.■

При фиксированном $n$ производящая функция чисел сочетаний с повторениями из $n$ по $k$ равна

$\sum _{k=0}^{\infty }\left[(-1)^{k}{-n \choose k}\right]x^{k}=(1-x)^{-n}.$

Двумерной производящей функцией чисел сочетаний с повторениями является

$\sum _{n=0}^{\infty }\sum _{k=0}^{\infty }(-1)^{k}{-n \choose k}x^{k}y^{n}=\sum _{n=0}^{\infty }(1-x)^{-n}y^{n}={\frac {1-x}{1-x-y}}.$

См. также

• Комбинаторика
• Многочлен
• Мультиномиальный коэффициент
• Перестановка
• Размещение

Ссылки

• Р. Стенли. Перечислительная комбинаторика. — М.: Мир, 1990.