Угол, опирающийся на диаметр окружности

$\angle ABC$ — прямой

Теоремой Фалеса в западной литературе называют следующее утверждение планиметрии:

Плоский угол, опирающийся на диаметр окружности, — прямой.

Данное утверждение является частным случаем свойства вписанных углов и поэтому тривиально.

Использование

Построение касательных с помощью угла, опирающегося на диаметр окружности

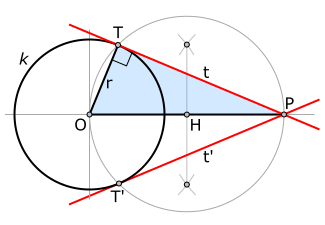
Используя свойство угла, опирающегося на диаметр, можно построить касательную к окружности. Пусть дана окружность $k$ и точка $P$ вне этой окружности, построим касательные из точки $P$ к окружности $k$. Построив центр $O$ окружности $k$, соединим его с точкой $P$ и на $OP$, как на диаметре, построим окружность. Т.к. две окружности пересекаются по двум точкам получим $T$ и $T'$. $\angle OTP$ будет прямой, т.к. вписанный и опирается на диаметр. $OT$ — радиус окружности $k$, перпендикулярный прямой $PT$, пересекающей окружность $k$ в точке $T$; следовательно, $PT$ — касательная. Аналогичные рассуждения можно провести о точке $T'$.