Фильтр Габора
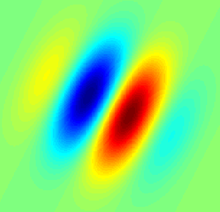
Фильтр Габора — линейный электронный фильтр, импульсная переходная характеристика которого определяется в виде гармонической функции, помноженной на гауссиан. При цифровой обработке изображений этот фильтр применяется для распознавания границ объектов.
Из-за свойства соответствия свёртки во временной области умножению в частотной области, преобразование Фурье импульсной передаточной характеристики фильтра Габора является свёрткой преобразований Фурье гармонической функции и гауссиана.
где
В этом уравнении представляет собой длину волны множителя-косинуса, определяет ориентацию нормали параллельных полос функции Габора в градусах, — сдвиг фаз в градусах и — коэффициент сжатия, характеризующий эллиптичность функции Габора.
Фильтры Габора напрямую связаны с вейвлетами Габора, так как они могут быть сконструированы путём ряда сжатий и вращений. Пространство Габора (свёртка фильтра с сигналом) часто применяется в различных приложениях обработки изображений, в частности, для распознавания радужной оболочки в биометрических системах безопасности и в автоматизированных системах контроля доступа на основании распознавания отпечатков пальцев.
Алгоритм построения одномерного фильтра Габора[править | править код]
Для построения одномерного фильтра Габора применяется формула:
,
- где:
- — стандартное отклонение Гаусового ядра, определяющее амплитуду функции;
- — частота колебаний, определяемая как , где:
- — период функции .
Чем больше , тем более пологий вид примет функция. Чем меньше , тем более острый пик получится в результате построения графика функции.
Приведённая выше функция экспоненты обладает свойствами нормального распределения случайной величины. Согласно правилу трёх сигм, практически все значения экспоненты лежат в интервале . Для анализа сигналов, значения функции рассчитываются в указанных пределах.
-
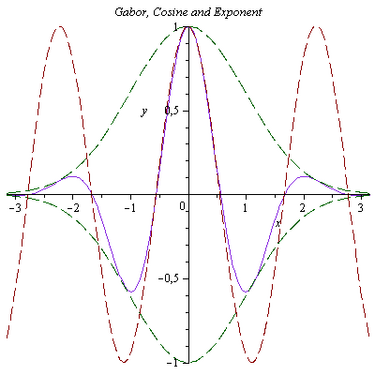
Косинус, экспонента и их композиция в функцию Габора
-
Зависимость функции от
-
Зависимость функции от
Обработка одномерного сигнала фильтром Габора[править | править код]
Каждая точка входного сигнала преобразуется в соответствующую точку выходного сигнала , путём усреднения значений входного сигнала по области , с учётом весовых коэффициентов формулы Габора.
- где:
- — входное значение сигнала в точке ,
- — выходное значение сигнала в точке ,
- — значение функции Габора, .
Алгоритм построения двумерного фильтра Габора[править | править код]

Для построения двумерного фильтра Габора применяется формула:
- где:
- — стандартные отклонения гауссова ядра, по осям и , определяющие растянутость фильтра по осям,
- — частотная модуляция фильтра,
- — пространственная направленность фильтра, определяющая его ориентацию относительно главных осей.
Обработка двумерного изображения фильтром Габора[править | править код]


Обработка изображения фильтром Габора достигается путём усреднения значений обрабатываемого изображения по некоторой области в каждой точке. Соответственно, наложение фильтра Габора на изображение имеет вид:
где:
— интенсивность исходного изображения в точке ,
— интенсивность нового изображения в точке ,
— значение функции Габора, .
Если отбросить синусоидальную составляющую функции в фильтре Габора, он выродится в фильтр Гауссова размытия (Gaussian Blur). Поэтому очевидно, что эти два фильтра имеют практически одинаковый алгоритм применения, различающийся в некоторых деталях.
Из формулы Габора видно, что фильтр зависит от частоты и направления квазипериодической структуры изображения. Поэтому перед применением фильтра необходимо построить частотное и ориентационное поля для текущего изображения. Обычно для упрощения задачи рассчитывается средняя частота изображения, которая считается неизменной в каждой точке.
Для построения поля направлений может применяться несколько способов, наиболее быстрым из которых является дифференциальный метод, позволяющий построить четырёхградационное поле направлений.
Таким образом, имея частоту и 4 направления, предварительно строятся 4 фильтра Габора, по одному на каждое направление. После чего в каждой точке изображения происходит свертка фильтра с изображением по определённой области, что дает выходное значение нового изображения.
Фильтр Габора эффективен при обработке изображений со структурной избыточностью, имеющих квазипериодическую структуру. К ним относятся дактилоскопические изображения, изображения кристаллограмм и интерферрограмм. В живой природе подобный окрас нередко встречается у зебр, различных кошачьих (тигры, рыси, дымчатые коты), птиц (тетерева), рыб (лепоринус полосатый) и прочих представителей флоры и фауны.
Пример реализации[править | править код]
Вот пример реализации фильтра Габора для пакета Matlab:
function gb = gabor_fn(sigma_x, theta, lambda, psi, gamma)
sz_x = fix(6 * sigma_x); % исходя из значения сигмы получили размер ядра
sz_x = sz_x - mod(sz_x,2) + 1; % если четное - делаем нечетным
sz_y = fix(6 * sigma_x / gamma); % исходя из значения сигмы и коэф. сжатия получили второй размер ядра
sz_y = sz_y - mod(sz_y,2) + 1; % если четное - делаем нечетным
[x y] = meshgrid(-fix(sz_x/2):fix(sz_x/2), fix(-sz_y/2):fix(sz_y/2)); % задали область определения
% Поворот
x_theta = x*cos(theta) + y*sin(theta);
y_theta = -x*sin(theta) + y*cos(theta);
gb = exp(-.5 * (x_theta.^2/sigma_x^2 + gamma^2*y_theta.^2/sigma_x^2))* cos(2 * pi* x_theta./lambda + psi); % ядро
См. также[править | править код]
Литература[править | править код]
- Сойфер В.А. Методы компьютерной обработки изображений. — Физматлит, 2003. — С. 459.
- Храмов, А. Г. Методы восстановления интерферрограмм на ЭВМ. — КуАИ, 1988. — С. 88.












![{\displaystyle [-3\sigma ;3\sigma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b0a8c6a6163fccda7c05ddc7a10caf9272b1769)
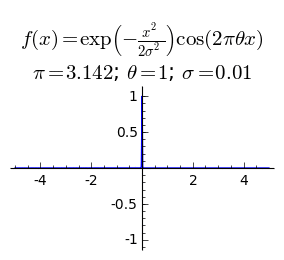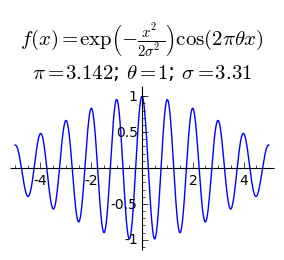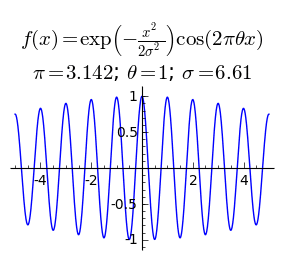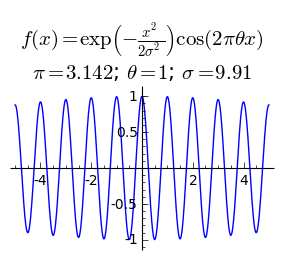





![{\displaystyle t\in [x-{\frac {n}{2}},x+{\frac {n}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea21038f3067a0ecb2829a563ddc488107a2cfd4)



![{\displaystyle i\in [0,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9242106e18dfff6aaf5c3150d134e96615dbe2fc)
![{\displaystyle G(x,y)=\exp \left(-{\frac {1}{2}}\left[{\frac {x_{\phi }^{2}}{\sigma _{x}^{2}}}+{\frac {y_{\phi }^{2}}{\sigma _{y}^{2}}}\right]\right)\cos(2\pi \theta x_{\phi })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85376bf5b37d1e27c1a64ec658a154c87fcff718)










![{\displaystyle i\in [0,n],j\in [0,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc24bd258bba271ec4b712094782eabc04349b7d)