Равновесие, совершенное по подыграм

Равновесие, совершенное по подыграм
Концепция решения в теории игр
Связанные множества решений
Надмножества	Равновесие Нэша
Подмножества	Эволюционно стабильная стратегия
Факты
Авторство	Рейнхард Зельтен
Применение	Игры в развёрнутой форме

Равновесие Нэша, совершенное по подыграм (англ. subgame perfect Nash equilibrium, SPNE) — концепция решения в теории игр, рафинирование равновесия Нэша для игр в развёрнутой форме.

Набор стратегий игроков называется равновесием, совершенным по подыграм, если его сужение на любую подыгру данной игры есть равновесие Нэша в ней. Интуитивно это означает, что действия сторон в некоторой игре будут одинаковы, независимо от того, разыгрывается ли она отдельно или является частью более общей надыгры.

Равновесие, совершенное по подыграм, позволяет отсеять равновесия Нэша, основанные на недостоверных угрозах игроков.

Распространённый метод решения — обратная индукция, при которой оптимизация ходов игроков начинается с конца игры. Данный метод не работает, если в игре отсутствуют подыгры, а также для повторяющихся игр с бесконечным горизонтом.

• 
  Игра в развёрнутой форме
• 
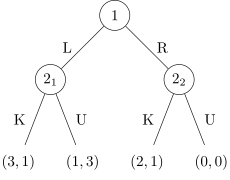
  Равновесие Нэша, несовершенное по подыграм
• 
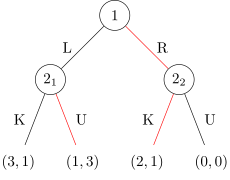
  Равновесие, совершенное по подыграм

См. также

Соотношение равновесных концепций решения. Стрелками обозначено направление от рафинирований к менее требовательным концепциям

• Некооперативная игра
• Равновесие Нэша

Литература

• Васин А. А., Морозов В. В. Теория игр и модели математической экономики. — М.: Макс-пресс, 2005. — 272 с. — ISBN 5-317-01388-7.
• Васин А.А. Некооперативные игры в природе и обществе. М.: Макс Пресс, 2005, 412 с. ISBN 5-317-01306-2.
• Петросян Л. А., Зенкевич Н.А., Семина Е.А. Теория игр: Учеб. пособие для ун-тов. — М.: Высш. шк., Книжный дом «Университет», 1998. — С. 304. — ISBN 5-06-001005-8, 5-8013-0007-4.
• Печерский С. Л., Беляева А. А. Теория игр для экономистов. Вводный курс. Учебное пособие. — СПб.: Изд. Европейского университета в Санкт-Петербурге, 2001.

Ссылки

• Пример игры в развернутой форме с несовершенной информацией
• Java-апплет для отыскания совершенного по подыграм равновесия с gametheory.net.
• Пример равновесия, совершенного по подыграм  (недоступная ссылка с 13-05-2013 [3989 дней] — история)