Взаимно простые числа

В «лесу», составленном на координатной плоскости из точек с целочисленными координатами, из начала координат «видны» только «деревья» со взаимно простыми координатами.

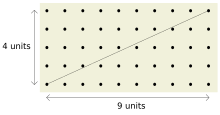
Взаимно простые числа — целые числа, не имеющие никаких общих делителей, кроме ±1. Равносильное определение: целые числа взаимно просты, если их наибольший общий делитель (НОД) равен 1.

Например, взаимно просты числа 14 и 25, так как у них нет общих делителей; но числа 15 и 25 не взаимно просты, так как у них имеется общий делитель 5. Для указания взаимной простоты чисел $m$ и $n$ иногда используется обозначение $m\perp n$ (аналогия с перпендикулярными прямыми, не имеющими общих направлений — взаимно простые числа не имеют общих сомножителей).

Для определения того, являются ли два числа взаимно простыми, можно использовать алгоритм Евклида.

Понятие взаимной простоты естественным образом обобщается на любые евклидовы кольца.

Свойство взаимной простоты не только играет важную роль в теории чисел и коммутативной алгебре, но имеет ряд важных практических приложений, в частности, число зубьев на звёздочках и число звеньев цепи в цепной передаче стремятся делать взаимно простыми, что обеспечивает равномерность износа: каждый зуб звёздочки будет поочерёдно работать со всеми звеньями цепи.

Попарно взаимно простые числа

Если в наборе целых чисел любые два числа взаимно просты, то такие числа называются попарно взаимно простыми (или просто попарно простыми). Для двух чисел понятия «взаимно простые» и «попарно простые» совпадают для более чем двух чисел свойство попарной простоты более сильно, чем ранее определённое свойство взаимной простоты (в совокупности) — попарно простые числа будут и взаимно простыми, но обратное неверно. Примеры:

• 8, 15 — не простые, но взаимно простые.
• 6, 8, 9 — взаимно простые (в совокупности) числа, но не попарно простые.
• 8, 15, 49 — попарно простые и взаимно простые (в совокупности).

Если числа $a_{1},\ldots ,a_{n}$ — попарно простые числа, то их наименьшее общее кратное равно абсолютному значению их произведения: $|a_{1}\cdot \ldots \cdot a_{n}|$. Имеет также место для любого $b$ формула:

НОД$(a_{1},a_{2},\dots ,b)=$ НОД$(a_{1},b)$ НОД$(a_{2},b)\dots$ НОД$(a_{n},b)$

Свойства

Все упомянутые в этом разделе числа подразумеваются целыми, если не оговорено иное.

Количество натуральных чисел, взаимно простых с натуральным числом $n$, задаётся функцией Эйлера φ(n).

Числа $a$ и $b$ взаимно просты тогда и только тогда, когда существуют целые $x$ и $y$ такие, что $ax+by=1$ (соотношение Безу). Если натуральные числа $a$ и $b$ взаимно просты, то числа $2^{a}-1$ и $2^{b}-1$ также взаимно просты, притом верно и обратное.

(Лемма Евклида) Если $a$ — делитель произведения $bc$, и $a$ взаимно просто с $b$, то $a$ — делитель $c$.

Если $d=$ НОД$(a,b)$, то числа ${\frac {a}{d}}$ и ${\frac {b}{d}}$ взаимно просты.

Дробь является несократимой тогда и только тогда, когда числитель и знаменатель взаимно просты.

Если числа $a$ и $m$ взаимно просты, то сравнение:

$ax\equiv b{\pmod {m}}.$

для любого $b$ имеет единственное решение по модулю $m.$ В частности, решение сравнения для $b=1$ даёт обратный элемент для $a$ в кольце вычетов по модулю m.

Вероятность того, что любые $k$ случайным образом выбранных положительных целых чисел будут взаимно просты, равна ${\dfrac {1}{\zeta (k)}}$, в том смысле, что при $N\to \infty$ вероятность того, что $k$ положительных целых чисел, меньших, чем ${\textstyle {N}}$ (и выбранных случайным образом) будут взаимно простыми, стремится к ${\dfrac {1}{\zeta (k)}}$. Здесь $\zeta (k)$ — это дзета-функция Римана.

Вариации и обобщения

Понятия простого числа, наибольшего общего делителя и взаимно простых чисел естественно обобщаются на произвольные евклидовы кольца, например, на кольцо многочленов или гауссовы целые числа. Обобщением понятия простого числа является «неприводимый элемент». Данное выше определение взаимно простых чисел не годится для произвольного евклидова кольца, поскольку в кольце могут быть делители единицы; в частности, НОД определяется с точностью до умножения на делитель единицы. Поэтому определение взаимно простых чисел следует модифицировать.

Элементы евклидова кольца называются взаимно простыми, если множество их наибольших общих делителей содержит только делители единицы.

Равносильные формулировки:

• Элементы евклидова кольца взаимно просты, если они не имеют никаких общих делителей, кроме делителей единицы.
• (Соотношение Безу) Элементы $a,b$ евклидова кольца $K$взаимно просты тогда и только тогда, когда существуют элементы $u,v\in K$ такие, что $au+vb=1.$

Имеет также место лемма Евклида.

Литература

• Взаимно простые числа // Большая советская энциклопедия : в 66 т. (65 т. и 1 доп.) / гл. ред. О. Ю. Шмидт. — М. : Советская энциклопедия, 1926—1947.
• Михелович Ш. Х. Теория чисел. — 2-е изд. — М.: Высшая школа, 1967. — 336 с.