Синхронизация (нейробиология)

В нейробиологии синхронизацией (от греч. συνχρόνος — одновременный) называют динамический режим, который характеризуется периодической одновременной активацией определенной популяции нейронов, или синхронизацию между локальными колебаниями двух или нескольких популяций нейронов.
Синхронизированная активность больших популяциях нейронов является главным механизмом образования макроколебаний, или так называемых ритмов головного мозга человека. Известно, что ритмы играют важную роль в процессах передачи и обработки информации в центральной нервной системе (сон, память, внимание, пространственная навигация и т. д.), однако общей теории относительно точного назначения и принципов работы ритмов пока нет.
С другой стороны, чрезмерная локальная синхронизация в некоторых сетях имеет патологические проявления, такие как тремор в болезни Паркинсона, эпилептические припадки, а также некоторые расстройства высшей мозговой функции (шизофрения, аутизм, и т. д.).
Важная роль синхронизации в процессах обработки информации в мозге делает её очень привлекательной темой исследований в медицинской и вычислительной нейронауке. Методы математического моделирования синхронизации (часто заимствованные из физики) в сочетании с доступностью вычислительных мощностей создают благоприятные условия для прогресса в направлении более глубокого и разностороннего понимания этого явления.
Вследствие того, что термин «синхронизация» является довольно распространённым и часто используется в различных отраслях науки, его точное определение может сильно варьировать в зависимости от конкретной сферы применения. В биологическом контексте удобно различать два вида синхронизации[1]:
- локальная синхронизация, синхронизация активности отдельной популяции нейронов, которая приводит к образованию макроколебаний и может становиться заметной в сигнале ЭЭГ
- фазовая синхронизация, синхронизация фазы макроколебаний между удалёнными участками мозга или группами нейронов
Во всех секциях настоящей статьи, за исключением секции «Математическое моделирование», будем использовать именно вышеприведенное определение термина «фазовая синхронизация».
С другой стороны, в детальном математическом моделировании локальной синхронизации принято использовать термин «фазовая синхронизация» в более абстрактном смысле. А именно, два или несколько осцилляторов фазово синхронизированы, если соответствие их фаз не меняется со временем[2], или, в наиболее общем определении, зависит по какой-либо функции. Причём амплитуды колебаний вышеупомянутых осцилляторов не обязательно должны быть одинаковы. Такими осцилляторами могут моделироваться как индивидуальные нейроны, так и сети или большие популяции нейронов. В секции «Математическое моделирование» описано несколько типов синхронизации.
Роль в работе ЦНС[править | править код]
Ритмы головного мозга[править | править код]

Электроэнцефалография (ЭЭГ) — один из ключевых неинвазивных методов исследования головного мозга, который характеризуется высоким временным разрешением, но низкой пространственной разрешающей способностью, особенно в сравнении с МРТ или инвазивными электродными методами. Из-за низкого пространственного разрешения (обычно не более 100 каналов), полученный сигнал является результатом суперпозиции активности крупных популяций нейронов, а значит, является удобным методом для нахождения и исследования синхронизированных коллективных режимов в сетях головного мозга. Синхронизация достаточно большой популяции нейронов обычно производит глобальные колебания, которые и записываются электродами электроэнцефалографа.
В большинстве случаев сильная глобальная синхронизация больших популяций (синхронизация типа I) присуща состоянию бездействия или патологическому состоянию, поскольку динамика полностью синхронизированной сети недостаточно сложна для эффективной обработки информации. Во время нормальной работы (кроме состояния глубокого сна) небольшие локально-синхронизированные подсети генерируют колебания разных частот (синхронизация типа II), при этом глобальная синхронизация исчезает[4]. Таким образом, спектр ЭЭГ сигнала содержит несколько важных составляющих, которые принято классифицировать по частоте, назначая каждому диапазону греческую букву. В таблице ниже приведено краткое описание каждого из ритмов согласно традиционной системе классификации, а также их соответствующие функции.
В следующих секциях более подробно рассмотрены свойства и пути образования некоторых ритмов.
| Ритм | Частота (Гц) | Типичное местонахождение | Обычные проявления | График |
|---|---|---|---|---|
| Дельта | 0 — 4 | Фронтально у взрослых, постериально у детей; волны высокой амплитуды |
|
|
| Тета | 4 — 7 | Гиппокамп, кора |
|
|
| Альфа | 8 — 12 | Постериальные участки головы, с обеих сторон, но с большей амплитудой на недоминантной стороне. Центральные локации (c3-c4) во время отдыха |
|
|
| Бета | 13 — 30 | Обе стороны, больше всего фронтально; волны малой амплитуды |
|
|
| Гамма | 30 — 100+ | Соматосенсорная кора |
|
|
| Мю | 8 — 13 | Соматосенсорная и моторная кора |
|
Кроме вышеупомянутых канонических ритмов, сигнал ЭЭГ может также содержать высокочастотные компоненты с частотой свыше 400 Гц. В большинстве случаев такие компоненты имеют очень низкую энергию и часто игнорируются или воспринимаются как шум. Однако недавние исследования показали, что высокочастотные колебания в сигнале ЭЭГ, которые можно наблюдать в соматосенсорной коре головного мозга в ответ на стимуляцию периферийного нерва, могут быть результатом очень точной синхронизации нейронных всплесков в соответствующих сетях[9]. В экспериментах с одновременным получением ЭЭГ и значения внешнеклеточного сигнала было показано, что форма высокочастотных компонентов сигнала ЭЭГ содержит информацию о временной структуре всплеска спайков индивидуальных нейронов. Таким образом, высокочастотные ритмы ЭЭГ могут пролить свет на динамику клеточного уровня без вмешательства в биологические ткани[9].
Центральные генераторы упорядоченной активности[править | править код]
Синхронизированная активность нейронов является базой для генерации периодических моторных команд для ритмических движений. Ритмичные команды, в свою очередь, производятся группой связанных нейронов, которые формируют сеть под названием центральный генератор упорядоченной активности (ЦГУА). При активации такие нейронные сети могут генерировать сложные ритмические моторные команды, даже при отсутствии сигналов обратной связи, которые несут информацию о конкретных временных интервалах. Ходьба, плавание или дыхание являются примерами работы ЦГУА[10]. ЦГУА наиболее исследованы у низших животных, таких как минога, однако также существуют свидетельства о наличии ЦГУА у людей[11].
Память[править | править код]
Фазовая синхронизация (ФС) колебаний между различными зонами мозга имеет ряд важных функций, которые являются критическими для эффективной работы памяти. Важной функцией является улучшение передачи информации между удалёнными участками мозга во время ФС[1]. Оптимальная передача информации может происходить благодаря ФС следующим образом: высокий уровень локального потенциала обычно свидетельствует о высоком уровне активности в локальной популяции в данный момент времени. В то же время чувствительность нейронов этой популяции также повышена, потому что мембраны нейронов в среднем более деполяризованы, чем когда локальный потенциал имеет низкие значения. Таким образом, если две удаленные популяции нейронов имеют синхронизированные коллективные колебания, то момент повышенной активности одной популяции совпадет с высокой возбудимостью другой, обеспечивая высокую вероятность передачи информации[12].
ФС также может способствовать усилению синаптической пластичности. Синаптическая пластичность, которая зависит от времени импульса (англ. Spike-Timing Dependent Plasticity, STDP) влечёт долговременную потенциацию синапсов, если принимающий нейрон срабатывает не более чем через 10-20 мс после входного импульса. ФС может обеспечить достаточно узкие интервалы срабатывания нейронов между двумя группами и таким образом увеличить или уменьшить силу связи между ними[1].
По распространённой системе классификации, существуют два основных вида памяти:
В работе кратковременной памяти ФС наблюдается между префронтальной корой и височной долей мозга (на частоте θ-ритма) во время чтения, записи и удержания краткосрочных воспоминаний, а также между фронтальными и париетальными зонами коры (на γ и β-частотах) во время удержания воспоминаний. Запись и чтение визуальных объектов из декларативной памяти (тип долговременной памяти) сопровождаются фазовой синхронизацией колебаний между передними и задними зонами мозга на θ, γ, δ и β-частотах. Другие виды синхронизации также принимают участие в презентации объектов в памяти[1].
Результаты экспериментов с одновременной записью электрической активности в гиппокампе и миндалине свидетельствуют об усилении синхронизации на θ-частотах между этими участками после формации и во время действия условного рефлекса страха[13].
Сон[править | править код]

Во время глубокой фазы сна, а также при некоторых видах анестезии на энцефалограммах обычно наблюдаются колебания низкой частоты (0,3 — 1 Гц) и дельта-колебания. Такие ритмы часто ассоциируются с отсутствием сознания, а также часто используются как индикатор наличия сознания у пациента под наркозом. На клеточном уровне осцилляции выглядят как периодическая смена состояний активного срабатывания нейронов и тишины, каждый из которых длится до одной секунды[14]. Одним из возможных механизмов генерации медленных колебаний (до 1 Гц) является совместная работа соответствующих сетей таламуса и неокортекса следующим образом:
- активность нейронов в коре инициирует внутренние осцилляции в таламусе
- колебания в таламусе усиливают синхронизацию тормозных интернейронов
- активация тормозных интернейронов подавляет активность нейронов кортекса, и наступает период тишины
- цикл повторяется
Другие механизмы образования низкочастотных колебаний хорошо освещены в работе, например, Г. Тимофеева[14].
При нормальных условиях, глубокий сон играет важную роль в процессах консолидации памяти. Согласно популярной теории, медленные коллективные колебания регулируют ре-активацию и транспорт воспоминаний от гиппокампа к кортексу. Во время фазы быстрого сна (повышенная тета-активность и локальная синаптическая пластичность), ре-активированные воспоминания в кортексе закрепляются на синаптическом уровне, то есть откладываются в долговременную память[15] [16].
Внимание[править | править код]
Внимание — направленность психической деятельности человека или животного и её сосредоточенность в определённый момент на объектах или явлениях, которые имеют определённое значение при одновременном абстрагировании от других, в результате чего они отображаются полнее, яснее и глубже, чем другие[17]. Во время концентрации внимания на конкретном объекте или его свойстве, повышается скорость обработки информации, уменьшается время реакции, повышается уровень точности, чувствительности к небольшим изменениям в стимуле и восприятие контраста.
Во-первых, внимание усиливает активность нейронов, которые представляют объект внимания или определенную характеристику (цвет, ориентация). Так, например, нейроны зрительной коры, рецептивное поле которых содержит объект внимания, сильнее синхронизированы с локальным потенциалом (на γ-частоте), чем нейроны, которые реагируют на другие объекты вне внимания. Такой способ селективного усиления синхронизации предположительно является альтернативой повышению частоты срабатывания нейронов (она обычно не меняется в зависимости от направления внимания)[18].
Во-вторых, внимание также регулирует информационное сообщение между отдалёнными частями мозга, усиливая связь между группами нейронов, которые несут важную для животного информацию. Многие исследования приходят к выводу что такое усиление связи происходит за счет селективной синхронизации между зонами коры[19].
Патология[править | править код]
Во время нормальной работы мозга, локальная и межзонная синхронизации нейронной активности играют важную роль в таких ключевых процессах, как внимание, память, моторика и т. д. Однако важным является также и определенный баланс синхронизации и десинхронизации[20]. Чрезмерная или недостаточная синхронизация может быть причиной многих патологических процессов, в числе которых эпилепсия, тремор, шизофрения, деменция и некоторые другие. Таким образом, важным направлением развития нейронауки является поиск эффективных путей обезвреживания патологической синхронизации и понимание принципов её создания.
Связанные заболевания[править | править код]
Эпилепсия[править | править код]

Эпилепсия характеризуется внезапным началом синхронизации в относительно больших нейронных сетях, в результате чего становится невозможной эффективная обработка информации, что в свою очередь препятствует нормальной работе мозга. Эпилептические припадки могут сопровождаться кратковременной потерей сознания или более сложными сенсорными и моторными проявлениями[20]. Наиболее проблематичным следствием эпилепсии является непредсказуемость припадков, вследствие чего людям, страдающим эпилепсией, может быть на законодательном уровне запрещено управлять транспортными средствами и выполнять некоторые другие занятия, требующие постоянного внимания.
Точные нейронные механизмы эпилептической синхронизации пока в совершенстве не известны. Однако применение теории динамических систем анализа и моделирования сигнала, который генерируется такими сетями, даёт определённые результаты в направлении понимания феномена. Любая нейронная сеть может быть описана как (нелинейная) динамическая система с одним или несколькими атракторами. (Аттрактор — это множество точек в фазовом пространстве системы, в котором сходятся траектории системы. Другими словами, это тип поведения, когда система возвращается в исходное состояние после небольшого отклонения в результате внешнего вмешательства. Простейшим примером аттрактора является предельный цикл. На таком атракторе система начинает описывать периодические колебания). Согласно одной из теорий, переход от нормальной к эпилептической активности сети может быть двух видов[21]:
- В результате постепенной деформации аттрактора нормальной активности в аттрактор эпилептической активности (через соответствующую бифуркацию), вследствие изменения параметров системы (например, внеклеточной концентрации ионов кальция или магния), или внешнего стимула. Такая модель соответствует типам припадков, когда изменение состояния протекает постепенно, в несколько фаз.
- Вследствие резкого «перескакивания» с одного нормального аттрактора на аттрактор синхронизированной активности, что было вызвано случайной флуктуацией или внешним стимулом (например, вспышками света). В отличие от первого случая, здесь система одновременно имеет два или несколько аттракторов, включая нормальные и эпилептические (такую систему называют мультистабильной). В этом случае, в мозге здорового человека такие аттракторы могут быть расположены дальше друг от друга, что делает невозможным случайный переход в состояние эпилептического припадка).
В зависимости от типа эпилепсии, могут быть применены различные подходы к моделированию динамических процессов, приводящих к массовой синхронизации нейронов[14] [21] [22].
Болезнь Паркинсона[править | править код]

Болезнь Паркинсона — это медленно прогрессирующее двигательное возбуждение, которое сопровождается нарушением речи, скованностью, повышением тонуса мышц, тремором и ригидностью мышц, замедлением движений. Тремор, который характеризуется ритмичными неконтролируемыми движениями конечностей, является очень проблематичным симптомом, так как, при определенных условиях, делает невозможным выполнение больным многих повседневных действий, таких как управление авто, удержание открытой ёмкости с жидкостью, рукописание и т. д.
Патологический процесс при этом заболевании характеризуется деградацией дофаминергических нейронов чёрного вещества, что влечёт за собой усиление активности и синхронизации нейронов в субталамических ядрах (часть базальных ганглий) и приводит к чрезмерному торможению таламо-кортикальной связи.
На настоящий момент точные механизмы генерации тремора у пациентов с болезнью Паркинсона неизвестны. Однако всё больше данных корреляционного характера свидетельствуют о связи между абнормально синхронизированной активностью в определённых частях мозга и мышечным тремором[23] [24]. Так, в соответствии с ведущей гипотезой, тремор генерируется группой нейронов в базальных ядрах, которые работают как центральные осцилляторы и продуцируют периодические импульсы определённым группам мышц. Причём важным является как общий уровень активности центральных осцилляторов, так и уровень их фазовой синхронизации[23].
Когнитивные расстройства[править | править код]
Шизофрения — это когнитивное расстройство, главными симптомами которого являются галлюцинации, сильно искажённое восприятие реальности и общая дезорганизация мышления и действий. Как и в случае с многими сложными ментальными заболеваниями, патофизиология шизофрении до сих пор остаётся до конца не известной[25].
Как известно, осцилляторная активность сетей головного мозга связана с такими важными процессами, как селективность к внешним стимулам с помощью внимания, памяти и сознания. Так как симптомы шизофрении связаны именно с расстройствами вышеупомянутых процессов, есть основания считать, что анормально низкая β и γ-синхронизация, которая наблюдается у больных, является важным фактором в патофизиологии заболевания. Современные эмпирические данные свидетельствуют о нелокальном и системном характере дисфункции головного мозга, которая возникает при шизофрении и может включать в себя расстройство в динамике нейронных сетей в префронтальных и теменных зонах, а также ухудшение связей между отдалёнными зонами[25][26].
Аутизм, заболевание, которое подавляет социальную и коммуникативную способности пациентов, также связано с уменьшенной осиляторной активностью на γ-частотах. Больные аутизмом страдают суженным фокусом внимания и не способны достаточно хорошо интегрировать фрагменты информации в единое целое, что может быть следствием недостаточно эффективной передачи информации между зонами мозга[25][26].
Методы борьбы[править | править код]
Фармацевтические[править | править код]
Одним из распространённых типов фармацевтического подавления чрезмерной синхронизации является использование разнообразных блокаторов ионных каналов, вследствие чего уменьшается возбудимость целевых нейронов или же угнетаются синаптические связи. Например, увеличение внеклеточной концентрации Mg2+ может прекращать синхронизированную колебательную активность в моделях эпилепсии. С одной стороны, это происходит благодаря способности ионов магния блокировать НМДА-рецепторы в синаптических связях между нейронами. С другой стороны, магний и некоторые другие 2- и 3-валентные ионы (например, Ca2+) могут влиять на локальный заряд вокруг натриевых и калиевых потенциалчувствительных каналов, снижая активационный порог и некоторые динамические характеристики нервной клетки[27] [28].
Фармацевтических средства также могут действовать через связывание и деактивацию определённых нейротрансмиттеров.
Хирургические[править | править код]
Почти треть пациентов с эпилепсией не показывают положительной динамики в результате лечения антиэпилептическими медикаментами[29]. Однако в некоторых случаях (около 7-8 %), удаётся достаточно точно локализовать источник анормальной эпилептической синхронизации в мозге, который удаляется с помощью оперативного вмешательства. Современные хирургические методы также позволяют проведение операций по удалению чрезмерно синхронизированных популяций в глубоком сером веществе (бледный шар, субталамические ядра) для устранения симптомов многих моторных заболеваний, включая болезнь Паркинсона[30].
Метод глубокой стимуляции мозга[править | править код]

Развитие компьютерных технологий открыло новую эру в лечении пациентов, страдающих болезнью Паркинсона. Всё чаще применяется новый метод глубокой стимуляции мозга (ГСМ). Метод ГСМ заключается в использовании импульсов электрического стимулятора, встроенного поверхностно в организм пациента. Через введённый в мозг специальный электрод импульсы подаются в базальные ганглии, в частности, в субталамические ядра, и выполняют высокочастотную стимуляцию групп нейронов, что приводит к заметному улучшению перенесения болезни. Вследствие существенного ослабления симптомов болезни, пациенты могут вернуться к нормальной повседневной деятельности и значительно уменьшить объём употребления лекарств. Кроме болезни Паркинсона, показаниями к операции являются врожденные дистония и эссенциальный тремор[31]. Также продолжаются клинические испытания для применения ГСМ в лечении депрессии.
Несмотря на большой успех ГСМ в лечении многих болезней, технология пока находится на раннем этапе развития, и полный отказ от хирургических вмешательств на пользу ГСМ является темой дебатов[30].
Математическое моделирование[править | править код]
Мотивация[править | править код]
Методы математического моделирования физических и химических процессов нашли широкое применение в биофизике и нейронауке. Начиная от моделирования стохастической динамики отдельных ионных каналов и заканчивая сетями со сложной неоднородной топологией и миллионами нейронов, модели помогают учёным понять механизмы функционирования нервной системы на различных уровнях абстракции, а значит и найти новые пути лечения соответствующих заболеваний, и разрабатывать более умные алгоритмы и вычислительные машины. Главным назначением математической модели является устранение незначительных факторов какого-то процесса или наблюдения и кристаллизация именно того минимального набора механизмов, который является достаточным для объяснения данных в конкретном контексте. Правильно построенная модель позволяет тестировать интересные гипотезы и делать важные предсказания относительно работы той или иной системы. В контексте синхронизации, моделирование позволяет применять аналитические и вычислительные методы для оценки динамических режимов сети. Например, бифуркационный анализ детальной модели нейронной сети может помочь определить максимально допустимые значения физиологических параметров, которые не приведут к переходу сети в патологически синхронизированный режим.
Модели биологического нейрона[править | править код]
Биологический нейрон можно моделировать на различных уровнях абстракции, но суть многих моделей заключается в выделении квазипериодических свойств его динамики, то есть изображении нейрона как осциллятора определённого уровня сложности.
Модель Курамото[править | править код]
Модель соединённых осцилляторов Курамото[32] — одна из наиболее абстрактных моделей, предназначенных для исследования синхронизации колебаний в нейронных сетях (осцилляторы имеют только одну степень свободы — фазу колебаний, игнорируя амплитуду)[33]. Взаимодействия между такими осцилляторами описываются простой алгебраической формой (такой, как синус) и коллективно генерируют определённую картину глобальной активности. Модель Курамото и её расширения (такие как, например, добавление возможности формировать связи различной силы) широко используются для изучения колебательных процессов в мозге[34]. В частности, её удобно использовать для изучения механизмов синхронизации в группе связанных нейронов.
В простейшем виде, фаза () каждого из N нейронов задаётся следующим образом:
где это частота колебания i-го осциллятора, и — сила соединения и элемент матрицы соединений соответственно.
Благодаря простоте определения, можно относительно быстро симулировать динамику крупных популяций таких нейронов, а также находить аналитические решения в определённых случаях.
Спаечные модели[править | править код]
Спаечные модели нейронов используются в случаях, когда нельзя ограничиться только фазовой или частотной абстракцией нейрона, то есть когда необходимо учитывать амплитуду колебаний, и/или другие, более детальные аспекты работы биологического нейрона. Характерным свойством спаечных моделей является способность генерировать активность, приближённую к потенциалу действия (спайку). Такие сети бывают очень полезными, когда необходимо сделать предсказание относительно значений определённых биологических параметров, потому что в их математическое определение часто включены аналоги биологических параметров (например, динамика ионных каналов или концентрация определенных веществ во внеклеточной среде). Однако главным недостатком таких моделей является сложность и нелинейность их математического определения, что ограничивает возможности аналитических решений и требует существенных затрат компьютерного времени для вычислительных решений.
Обычно один такой нейрон определяется системой нелинейных дифференциальных уравнений. В вычислительной нейронауке наиболее популярными являются следующие модели:
- экспоненциальная импульсная модель (модель англ. integrate-and-fire: «интегрировать и возбуждаться», «интегрировать и сработать») (AdEx)[35]. Является простейшей моделью, которая способна продуцировать все основные динамические режимы биологического нейрона, такие как однократное срабатывание, регулярное срабатывание в ответ на стимуляцию постоянным током, пачечная активность и т. д. Широко используется в исследованиях синхронизации у крупных гетерогенных популяций нейронов. Описывается системой двух дифференциальных уравнений.
- Модель Хиндмарша — Роуза (HR) — одна из самых простых непрерывных моделей, которая способна генерировать пачечную, а также хаотичную активности. Описывается системой трёх дифференциальных уравнений[36].
- Модель Ходжкина — Хаксли (HH) и производные — семейство детальных биологически-реалистичных моделей нейронов, которые включают в себя кинетику натриевых, калиевых, кальциевых и других ионных каналов. Различные модификации способны очень точно имитировать форму потенциала действия настоящих нейронов. Система обычно описывается как минимум четырьмя нелинейными дифференциальными уравнениями. Несмотря на сложность математического определения, HH-подобные модели успешно используются для исследований эффектов синхронизации в больших популяциях нейронов[37].
Виды синхронизации осцилляторов[править | править код]
Существует большое количество различных определений явления синхронизации, которые могут быть применены в том или ином контексте. Отметим некоторые основные виды синхронизации
- Полная синхронизация — самый простой с математической точки зрения тип синхронизации, который характеризуется полной сходимостью соответствующих переменных всех нейронов в сети. Например, если i-й нейрон описывается вектором переменных , то говорят что сеть из N нейронов полностью синхронизирована, если её состояние соответствует уравнению . Состояние полной синхронизации может быть достигнуто только в сети с идентичными нейронами.
- Фазовая синхронизация накладывает определённые ограничения на фазовые отношения между осцилляторами, игнорируя отношение амплитуд. Если в системе можно определить понятие фазы, то фазовая синхронизация сети таких осцилляторов означает, что разность фаз между элементами сети должна или вообще не меняться со временем, или находиться в определённых конечных границах[38]. Такой подход позволяет исследовать синхронизацию сетей с осцилляторами, параметры которых могут отличаться.
- Обобщенная синхронизация подобна фазовой, только отношение между фазами должны описываться определённой функцией.
- Пачечная синхронизация — синхронизация нейронов во время пачечной активности. Такая синхронизация не требует точного совпадения моментов спайков нейронов, но требует синхронизированного срабатывания пачек спайков (ритмических, ограниченных во времени всплесков активности с генерацией нескольких потенциалов действия)[39].
Глобальная функция стабильности синхронизированного состояния[править | править код]

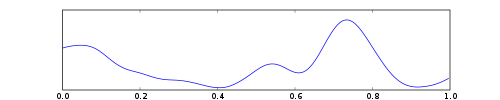
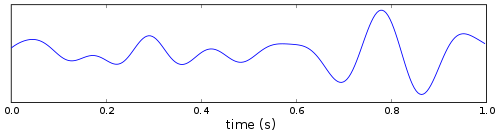
Верхняя панель: время срабатывания каждого из нейронов (серые точки).
Средняя панель: потенциал мембраны пяти случайно выбранных нейронов (у каждого свой цвет).
Нижняя панель: аппроксимация локального потенциала популяции (среднее значение НЧ-отфильтрованных потенциалов мембраны).
Простота математического определения состояния полной синхронизации делает возможным применение интересных аналитических методов для исследования этого вида синхронизации. Глобальная функция стабильности синхронизированного состояния (англ. Master Stability Function, MSF), например, позволяет определять стабильность состояния полной синхронизации для сети идентичных нейронов[40]. Другими словами, рассчитав MSF для сети нужных моделей нейронов, можно с точностью сказать, существуют ли такие топологии соединения нейронов, при которых данная сеть будет способна синхронизироваться (то есть будет иметь стабильное состояние полной синхронизации). Красота метода заключается в том, что MSF надо рассчитывать лишь один раз для каждого конкретного типа модели и набора параметров, а из результата можно делать выводы о стабильности синхронизированного состояния для любого количества нейронов и любой топологии (при соблюдении условия одинаковой суммарной силы входного сигнала для нейронов).
Основной процесс анализа синхронизации системы с помощью MSF можно разбить на несколько шагов. Рассмотрим сеть идентичных связанных нейронов, каждый из которых описывается определённой системой диф. уравнений (например, модель Ходжкина — Хаксли). Тогда сеть с N нейронами можно записать в таком виде:
где ; это D-мерный вектор переменных i-го нейрона (вектор состояния); и векторные поля, которые описывают соответственно (нелинейную) внутреннюю динамику (обычное мат. определение нейрона) и функцию связи между элементами; элемент матрицы , который содержит силы синаптических связей между нейронами.
Итак, общая размерность фазового пространства всей сети будет равна . Часто нужно анализировать сеть с большим количеством нейронов (), и тогда прямой анализ стабильности синхронизированного состояния сети (с помощью, например, экспонент Ляпунова) становится слишком громоздкой вычислительной задачей. С другой стороны, согласно формализму MSF, для определения стабильности синхронизированного состояния вышеприведённой системы, достаточно рассчитать экспоненты Ляпунова для гораздо меньшей, линеаризованной D-мерной системы, которая задаётся уравнением (предположим, что матрица связей имеет исключительно реальные собственные числа):
где якобиан векторного поля, рассчитанный вдоль синхронизированного решения (под синхронизированным решением здесь имеется в виду вычислительное решение уравнения одного нейрона, соединённого с самим собой), а — специальный скалярный параметр.
Опустив детали, имеем следующий алгоритм:
- Рассчитать максимальную экспоненту Ляпунова () небольшой линейной системы (2) для нужного диапазона параметра ;
- Построить график зависимости от параметра и определить диапазоны параметра, где имеет отрицательный знак;
- Найти собственные числа матрицы связей
- Если все собственные числа матрицы связей (за исключением того, которое равняется строковой сумме матрицы, см.[40]) попадают в диапазон , что соответствует отрицательной — сеть имеет стабильное состояние полной синхронизации
Пример графика MSF для HR нейронов, а также видео процесса полной синхронизации небольшой сети (согласно предсказанию MSF) приведены справа.
Примечания[править | править код]
- ↑ 1 2 3 4 Juergen Fell & Nikolai Axmacher. The role of phase synchronization in memory processes (англ.) // Nature reviews. Neuroscience : journal. — 2011. — February (vol. 12, no. 2). — P. 105—118. — doi:10.1038/nrn2979. — PMID 21248789.
- ↑ Фазовая синхронизация. Дата обращения: 7 декабря 2013. Архивировано 10 января 2014 года.
- ↑ S. J. van Albada & P. A. Robinson. Relationships between Electroencephalographic Spectral Peaks Across Frequency Bands (англ.) // Frontiers in human neuroscience : journal. — 2013. — Vol. 7. — P. 56. — doi:10.3389/fnhum.2013.00056. — PMID 23483663.
- ↑ W. Klimesch. Memory processes, brain oscillations and EEG synchronization (англ.) // International journal of psychophysiology : official journal of the International Organization of Psychophysiology : journal. — 1996. — November (vol. 24, no. 1—2). — P. 61—100. — PMID 8978436.
- ↑ 1 2 Kirmizi-Alsan, Elif; Bayraktaroglu, Zubeyir; Gurvit, Hakan; Keskin, Yasemin H.; Emre, Murat; Demiralp, Tamer. Comparative analysis of event-related potentials during Go/NoGo and CPT: Decomposition of electrophysiological markers of response inhibition and sustained attention (англ.) // Brain Research[англ.] : journal. — 2006. — Vol. 1104, no. 1. — P. 114—128. — doi:10.1016/j.brainres.2006.03.010. — PMID 16824492.
- ↑ Kisley, Michael A.; Cornwell, Zoe M. Gamma and beta neural activity evoked during a sensory gating paradigm: Effects of auditory, somatosensory and cross-modal stimulation (англ.) // Clinical Neurophysiology : journal. — 2006. — Vol. 117, no. 11. — P. 2549—2563. — doi:10.1016/j.clinph.2006.08.003. — PMID 17008125. — PMC 1773003.
- ↑ Kanayama, Noriaki; Sato, Atsushi; Ohira, Hideki. Crossmodal effect with rubber hand illusion and gamma-band activity (англ.) // Psychophysiology : journal. — 2007. — Vol. 44, no. 3. — P. 392—402. — doi:10.1111/j.1469-8986.2007.00511.x. — PMID 17371495.
- ↑ Gastaut, H. Electrocorticographic study of the reactivity of rolandic rhythm (англ.) // Revue neurologique[англ.] : journal. — 1952. — Vol. 87, no. 2. — P. 176—182. — PMID 13014777.
- ↑ 1 2 Bartosz Telenczuk, Stuart N. Baker, Andreas V. M. Herz & Gabriel Curio. High-frequency EEG covaries with spike burst patterns detected in cortical neurons (англ.) // Journal of neurophysiology[англ.] : journal. — 2011. — June (vol. 105, no. 6). — P. 2951—2959. — doi:10.1152/jn.00327.2010. — PMID 21490283.
- ↑ Marder E., Bucher D. Central pattern generators and the control of rhythmic movements (англ.) // Curr Biol : journal. — 2001. — Vol. 11. — P. R986—R996. — doi:10.1016/S0960-9822(01)00581-4.
- ↑ Dimitrijevic M. R., Gerasimenko Y., Pinter M. M. Evidence for a spinal central pattern generator in humans (англ.) // Ann NY Acad Sci[англ.] : journal. — 1998. — Vol. 860. — P. 360—376. — doi:10.1111/j.1749-6632.1998.tb09062.x. — PMID 9928325.
- ↑ Womelsdorf, T.; Schoffelen, J.-M.; Oostenveld, R.; Singer, W.; Desimone, R.; Engel, A. K.; Fries, P. Modulation of Neuronal Interactions Through Neuronal Synchronization (англ.) // Science : journal. — 2007. — Vol. 316, no. 5831. — P. 1609—1612. — ISSN 0036-8075. — doi:10.1126/science.1139597.
- ↑ Thomas Seidenbecher, T. Rao Laxmi, Oliver Stork & Hans-Christian Pape. Amygdalar and hippocampal theta rhythm synchronization during fear memory retrieval (англ.) // Science : journal. — 2003. — August (vol. 301, no. 5634). — P. 846—850. — doi:10.1126/science.1085818. — PMID 12907806.
- ↑ 1 2 3 Timofeev, I.; Bazhenov, M.; Seigneur, J. Neuronal Synchronization and Thalamocortical Rhythms in Sleep, Wake and Epilepsy (англ.) / Noebels, J. L.. — National Center for Biotechnology Information (US), 2012. — (History of the Second World War, United Kingdom Military Series). Архивировано 9 марта 2021 года.
- ↑ Diekelmann, Susanne; Born, Jan. The memory function of sleep (англ.) // Nature Reviews Neuroscience : journal. — 2010. — ISSN 1471-003X. — doi:10.1038/nrn2762.
- ↑ Diekelmann, Susanne; Born, Jan. Slow-wave sleep takes the leading role in memory reorganization (англ.) // Nature Reviews Neuroscience : journal. — 2010. — Vol. 11, no. 3. — P. 218—218. — ISSN 1471-003X. — doi:10.1038/nrn2762-c2.
- ↑ Украинская психологическая терминология: словарь-справочник. Под ред. М.-Л. А. Чепы. — К.: ГП «Информационно-аналитическое агентство», 2010. ISBN 978-617-571-040-0 (ошибоч.) .
- ↑ Fries, P. Modulation of Oscillatory Neuronal Synchronization by Selective Visual Attention (англ.) // Science : journal. — 2001. — Vol. 291, no. 5508. — P. 1560—1563. — ISSN 00368075. — doi:10.1126/science.1055465.
- ↑ Thilo Womelsdorf & Pascal Fries. The role of neuronal synchronization in selective attention (англ.) // Current opinion in neurobiology : journal. — 2007. — April (vol. 17, no. 2). — P. 154—160. — doi:10.1016/j.conb.2007.02.002. — PMID 17306527.
- ↑ 1 2 Alfons Schnitzler & Joachim Gross. Normal and pathological oscillatory communication in the brain (англ.) // Nature reviews. Neuroscience : journal. — 2005. — April (vol. 6, no. 4). — P. 285—296. — doi:10.1038/nrn1650. — PMID 15803160.
- ↑ 1 2 Fernando H. Lopes da Silva, Wouter Blanes, Stiliyan N. Kalitzin, Jaime Parra, Piotr Suffczynski & Demetrios N. Velis. Dynamical diseases of brain systems: different routes to epileptic seizures (англ.) // IEEE transactions on bio-medical engineering : journal. — 2003. — May (vol. 50, no. 5). — P. 540—548. — doi:10.1109/TBME.2003.810703. — PMID 12769430.
- ↑ Perez Velazquez, Jose L; Cortez, Miguel A; Snead, O.Carter; Wennberg, Richard. Dynamical regimes underlying epileptiform events: role of instabilities and bifurcations in brain activity (англ.) // Physica D: Nonlinear Phenomena[англ.] : journal. — 2003. — Vol. 186, no. 3—4. — P. 205—220. — ISSN 01672789. — doi:10.1016/j.physd.2003.07.002.
- ↑ 1 2 Bartolić, Andrej; Pirtošek, Zvezdan; Rozman, Janez; Ribarič, Samo. Tremor amplitude and tremor frequency variability in Parkinson’s disease is dependent on activity and synchronisation of central oscillators in basal ganglia (англ.) // Medical Hypotheses[англ.] : journal. — 2010. — Vol. 74, no. 2. — P. 362—365. — ISSN 03069877. — doi:10.1016/j.mehy.2009.06.057.
- ↑ R. Levy, W. D. Hutchison, A. M. Lozano & J. O. Dostrovsky. High-frequency synchronization of neuronal activity in the subthalamic nucleus of parkinsonian patients with limb tremor (англ.) // The Journal of neuroscience : the official journal of the Society for Neuroscience[англ.] : journal. — 2000. — October (vol. 20, no. 20). — P. 7766—7775. — PMID 11027240.
- ↑ 1 2 3 Peter J. Uhlhaas & Wolf Singer. Abnormal neural oscillations and synchrony in schizophrenia (англ.) // Nature reviews. Neuroscience : journal. — 2010. — February (vol. 11, no. 2). — P. 100—113. — doi:10.1038/nrn2774. — PMID 20087360.
- ↑ 1 2 Wang, X.-J. Neurophysiological and Computational Principles of Cortical Rhythms in Cognition (англ.) // Physiological Reviews[англ.] : journal. — 2010. — Vol. 90, no. 3. — P. 1195—1268. — ISSN 0031-9333. — doi:10.1152/physrev.00035.2008.
- ↑ B. Frankenhaeuser & A. L. Hodgkin. The action of calcium on the electrical properties of squid axons (англ.) // The Journal of physiology[англ.] : journal. — 1957. — July (vol. 137, no. 2). — P. 218—244. — PMID 13449874.
- ↑ Dmytro Isaev, Gleb Ivanchick, Volodymyr Khmyz, Elena Isaeva, Alina Savrasova, Oleg Krishtal, Gregory L. Holmes & Oleksandr Maximyuk. Surface charge impact in low-magnesium model of seizure in rat hippocampus (англ.) // Journal of neurophysiology[англ.] : journal. — 2012. — January (vol. 107, no. 1). — P. 417—423. — doi:10.1152/jn.00574.2011. — PMID 22031777.
- ↑ Klaus Lehnertz, Stephan Bialonski, Marie-Therese Horstmann, Dieter Krug, Alexander Rothkegel, Matthaus Staniek & Tobias Wagner. Synchronization phenomena in human epileptic brain networks (англ.) // Journal of neuroscience methods : journal. — 2009. — September (vol. 183, no. 1). — P. 42—48. — doi:10.1016/j.jneumeth.2009.05.015. — PMID 19481573.
- ↑ 1 2 Michael S. Okun & Jerrold L. Vitek. Lesion therapy for Parkinson's disease and other movement disorders: update and controversies (англ.) // Movement disorders : official journal of the Movement Disorder Society : journal. — 2004. — April (vol. 19, no. 4). — P. 375—389. — doi:10.1002/mds.20037. — PMID 15077235.
- ↑ Лечение болезни Паркинсона - метод глубокой стимуляции мозга. Дата обращения: 7 декабря 2013. Архивировано из оригинала 8 октября 2011 года.
- ↑ Kuramoto Y. Chemical Oscillations, Waves, and Turbulence (англ.). — Dover Publications, 1984.
- ↑ Ermentrout B. An introduction to neural oscillators (неопр.) // In F Ventriglia (ed.), Neural Modeling and Neural Networks. — 1994. — С. 79—110.
- ↑ Breakspear M., Heitmann S., Daffertshofer A. Generative models of cortical oscillations: Neurobiological implications of the Kuramoto model (англ.) // Front Hum Neurosc : journal. — 2010. — Vol. 4. — doi:10.3389/fnhum.2010.00190.
- ↑ Brette, R. Adaptive Exponential Integrate-and-Fire Model as an Effective Description of Neuronal Activity (англ.) // Journal of Neurophysiology[англ.] : journal. — 2005. — Vol. 94, no. 5. — P. 3637—3642. — ISSN 0022-3077. — doi:10.1152/jn.00686.2005.
- ↑ Hindmarsh, J. L.; Rose, R. M. A Model of Neuronal Bursting Using Three Coupled First Order Differential Equations (англ.) // Proceedings of the Royal Society B: Biological Sciences : journal. — 1984. — Vol. 221, no. 1222. — P. 87—102. — ISSN 0962-8452. — doi:10.1098/rspb.1984.0024.
- ↑ Golomb, D. Persistent Synchronized Bursting Activity in Cortical Tissues With Low Magnesium Concentration: A Modeling Study (англ.) // Journal of Neurophysiology[англ.] : journal. — 2005. — Vol. 95, no. 2. — P. 1049—1067. — ISSN 0022-3077. — doi:10.1152/jn.00932.2005.
- ↑ Brown, Reggie; Kocarev, Ljupčo. A unifying definition of synchronization for dynamical systems (англ.) // Chaos: An Interdisciplinary Journal of Nonlinear Science[англ.] : journal. — 2000. — Vol. 10, no. 2. — P. 344. — ISSN 10541500. — doi:10.1063/1.166500.
- ↑ Rubin, Jonathan. Burst synchronization (неопр.) // Scholarpedia. — 2007. — Т. 2, № 10. — С. 1666. — ISSN 1941-6016. — doi:10.4249/scholarpedia.1666.
- ↑ 1 2 Pecora, Louis M.; Carroll, Thomas L. Master Stability Functions for Synchronized Coupled Systems (англ.) // Physical Review Letters : journal. — 1998. — Vol. 80, no. 10. — P. 2109—2112. — ISSN 0031-9007. — doi:10.1103/PhysRevLett.80.2109.
Литература[править | править код]
- Buzsáki, György. Rhythms of the Brain (англ.). — Oxford University Press, 2006. — ISBN 978-0-19-530106-9.
- Скляров Олег Павлович. Нарушения ритма речи, возникающие в результате синхронизации, индуцированной в связанных осцилляторах // Техническая акустика : журнал. — 2005. — № 5. — С. 420—423.
- Бушов Юрий Валентинович, Светлик Михаил Васильевич. Фазовые взаимодействия между высокои низкочастотными ритмами ЭЭГ и их роль в когнитивных процессах // Вестник Томского государственного университета. Биология : журнал. — 2012. — № 3. — С. 137—145.
- Цукерман В.Д. Математическая модель фазового кодирования событий в мозге // Математическая биология и биоинформатика. — 2006. — Т. 1, № 1. — С. 97—107.
- Бушов Ю.В., Светлик М.В., Крутенкова Е.П. Гамма- активность коры головного мозга: связь с интеллектом и точностью восприятия времени // Физиология человека. — Академический научно-издательский, производственно-полиграфический и книгораспространительский центр РАН «Издательство „Наука“» (Москва), 2010. — Т. 36, № 4. — С. 15—21. — ISSN 0131-1646.










![{\displaystyle [\mathbf {x} _{1}(t)=\mathbf {x} _{2}(t)=\dots =\mathbf {x} _{N}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77950527919e1718b3f8ccb65b12821c0d5ba9ba)












![{\displaystyle {\dot {\mathbf {\zeta } }}=\left[D\mathbf {f} (\mathbf {x} _{s})+\alpha D\mathbf {h} (\mathbf {x} _{s})\right]\mathbf {\zeta } ,\qquad (2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19ae0715756cd4570ee95a34ec595e95a9346a97)




