Призма (оптика)
Материал из Википедии — свободной энциклопедии
В оптике призма - оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела - призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется.
Содержание |
[править] Виды призм
[править] Дисперсионные призмы
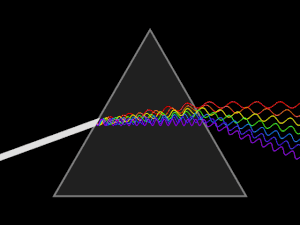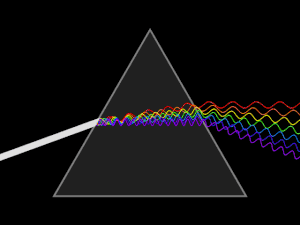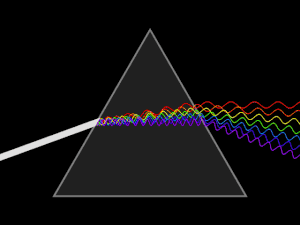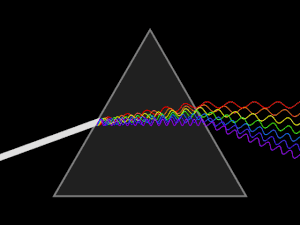
Дисперсионные призмы используют в спектральных приборах для пространственного разделения излучений различных длин волн.
- Простая трехгранная призма
- Призма Броунинга-Рузерфорда
- Дисперсионная призма Аббе
- Призма Амичи (призма прямого зрения)
[править] Отражательные призмы
Отражательные призмы используют для изменения хода лучей, изменения направления оптической оси, изменеия направления линии визирования, для уменьшения габаритных размеров приборов. Классифицируются отражательные призмы по нескольким признакам:
- количеству отражений в призме
- наличию или отсутствию «крыши»
- характеру конструкции призмы
- углу излома оптической оси
Также, особую нишу среди отражательных призм занимают составные призмы, — состоящие из нескольких частей, разделённых воздушными промежуткми. Некторые широкораспространённые призмы получили собственные имена.
- Пентапризма
- Призма Порро
- Призма Аббе-Порро
- Призма Аббе
- Призма Пехана-Шмидта
- Призма Дове
- Призмы с «крышей»
- Дихроидная призма
Название призмы обозначается двумя или тремя буквами и числом, записанным через дефис. Первая буква означает количесвто оражательных граней (отражений) в призме. («А» — одна, «Б» — две, «В» — три и т.д.). «Крыша», условно, считается одной гранью и для её обозначения ставят индекс «к» после первой буквы. (например, Ак, Бк) Оставшаяся буква укзывает характер конструкции. («Р» — равнобедренная, «П» — пентапризма, «У» — полупентапризма, «С» — ромбическая, «М» — дальномерного типа, «Л» — призма Лемана). Цифры, записанные через дефис указывают угол излома оптической оси. (0°,90°,180°). Например, «ВкР-45°» — равнобедренная призма с тремя отражательными гранями и крышей, с излмом оси на 45°.
Составные призмы указываются по их собственным именам и углам излома оси. Например, «А-0°» — Призма Аббе, «Бк-90°» — башмачная призма с крышей, «К-0°» — призма-куб.
[править] Поляризационные призмы
- Призма Николя
- Призма Волластона
- Призма Аренса
- Призма Глана-Фуко
- Призма Глазебрука
- Призма Рошона
[править] Путь лучей в призме
[править] Развёртка призм
[править] Ссылки
- Optics (4th ed.). — Pearson Education, 2001. — ISBN ISBN 0-8053-8566-5
